- ...existieren.
- Diese Annahme ist gerechtfertigt, da wir
zu Beginn vorausgesetzt haben, das die betrachteten Potentiale alle
schneller als r-1 gegen Null gehen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(LTFA)
- Die LTFA setzt voraus, daß die Wellenlänge des Elektrons
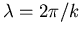 viel kleiner ist als die Reichweite des Störpotentials, die man
durch die Thomas-Fermi-Abschirmlänge L approximieren kann
(Anhang D).
Das führt auf die Bedingung
viel kleiner ist als die Reichweite des Störpotentials, die man
durch die Thomas-Fermi-Abschirmlänge L approximieren kann
(Anhang D).
Das führt auf die Bedingung
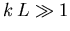 unter der das Elektron als klassisches Teilchen angesehen
werden kann. Die Bedingung impliziert ein langsam variierendes Potential
im Ortsraum verglichen mit der Wellenlänge des Elektrons. Diese
Annahme führt zur Abschirmlänge von Thomas-Fermi und Debye-Hückel,
die dadurch vom Impulsübertrag unabhängig wird [Din55,Man56,Mar57].
unter der das Elektron als klassisches Teilchen angesehen
werden kann. Die Bedingung impliziert ein langsam variierendes Potential
im Ortsraum verglichen mit der Wellenlänge des Elektrons. Diese
Annahme führt zur Abschirmlänge von Thomas-Fermi und Debye-Hückel,
die dadurch vom Impulsübertrag unabhängig wird [Din55,Man56,Mar57].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(RPA)
- Die RPA geht für kleines q über in die LTFA.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Streuung
- Bei der Untersuchung von Wellenphänomenen spricht man von Beugung
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...#3753#
- Der Integrationsbereich ist so zu wählen, daß die Ladungsdichte außerhalb
vernachlässigbar ist. Da in Kapitel 1 vorausgesetzt wurde, daß das Integral
konvergiert, kann der Bereich ins Unendliche ausgedehnt werden.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...nennen.)
- Auch in dem sehr umfassenden Review-Artikel über
Störstellenstreuung [CQ81] ist kein Hinweis auf den Formfaktor zu finden.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...werden
- Diese Näherung ist dann gerechtferigt, wenn Halbleiter und
Dotierstoff aus derselben Periode stammen, also die gleiche Anzahl an
Elektronenschalen besitzen, wie z.B. in P-dotiertem Silizium.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Halbleitern
- Wir betrachten in weiterer Folge dotiertes Silizium, wobei wir bei Konzentrationen
bis 1015 von niedriger, zwischen 1016-1017 von mittlerer und ab 1018 cm-3 von hoher Dotierung sprechen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...,,sieht``
- Bekanntlich wird jede Multipolladung in großer Entfernung zur Punktladung, da alle Momente höherer Ordnung verschwinden [Hof74].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Gradientenkorrektur
- Man ist sich nicht einig über den Koeffizienten des Korrekturterms.
Weizsäcker's Wert 0.125 wurde später auf ein Neuntel vermindert [KP57,Shi76], aber auch dieser Wert ist
umstritten, sodaß viele Autoren diesen Koeffizienten als Fitparameter ansehen
[YT65].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...kann
- In dieser Arbeit wird gezeigt,
daß dieser oft zitierte Mangel
der ersten Born-Näherung nicht ganz korrekt ist, da man über den Formfaktor sehr wohl unterschiedliche
Wirkungsquerschnitte und damit Beweglichkeiten erhält.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Modell
- Die Autoren haben über einen großen Dotierungsbereich die
ohmsche Beweglichkeit in P- und As-dotiertem Silizium bei 300 K gemessen. Basierend auf diesen Daten bei 300 K
wurde eine empirische Formel für jeden Donator angegeben. Da keinerlei
Daten über andere Temperaturen angegeben wurden, ist die Gültigkeit
der Formeln bei anderen Temperaturen äußerst fraglich.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...existiert
- Die resultierenden Beweglichkeiten für diesen Streuprozeß
weisen entweder keine oder nur eine sehr schwache Temperaturabhängigkeit auf.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...verliert
- Diskussionen über die Gültigkeit der Born-Näherung finden sich in [Dis32,MF53a,MB81]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Lösungsspektrum
- Diese Quantisierung bestimmter in der klassischen Physik kontinuierlich auftretender Größen verdankt die Quantenphysik ihren Namen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.