next up previous contents
Next: 1.4 Nanostructured Materials for Thermoelectrics Up: 1. Introduction Previous: 1.2 Device Efficiency   Contents


1.3 Thermoelectric Materials

Bismuth telluride $ \mathrm{Bi_2Te_3}$ , a narrow bandgap semiconductor, is one of the most commonly used thermoelectric materials [5]. It has been shown that by adding antimony telluride $ \mathrm{Sb_2Te_3}$ and bismuth selenide $ \mathrm{Bi_2Se_3}$ to $ \mathrm{Bi_2Te_3}$ , it is possible to obtain a $ ZT$ of around unity. In turn, it was shown that by alloying of $ \mathrm{Bi_2Te_3}$ with bismuth selenide and antimony telluride, the thermal conductivity decreases, without significant degradation of the electrical conductivity [3]. As mentioned in Sec. 1.2, working at high temperature is advantageous for energy conversion efficiency. However, the alloys of bismuth telluride are not suitable at temperature higher than $ 400~\mathrm{K}$ . Common thermoelectric materials for higher temperatures are lead telluride $ (\mathrm{PbTe})$ and silicon-germanium alloys. These materials have $ ZT$ between 0.5 and 1.1, depending on the temperature and the type of material (whether $ n$ -type or $ p$ -type) [3]. As a result, the average efficiency of current thermoelectric generators is about $ 5\%$  [6].

Good thermoelectric materials should simultaneously have a high Seebeck coefficient, a high electrical conductivity, and a low thermal conductivity. While each property of $ ZT$ can individually be changed by several orders of magnitude, the interdependence and coupling between these properties in bulk materials have made it extremely difficult to increase $ ZT>1$ . In the case of bulk materials, assuming the effective mass approximation and Fermi-Dirac statistics, one can relate the Seebeck coefficient and the electrical conductivity $ \sigma$ to the carrier concentration $ n$ as [6]:

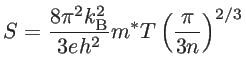$\displaystyle S=\frac{8\pi^2k_{\mathrm{B}}^2}{3eh^2}m^*T\left( \frac{\pi}{3n} \right)^{2/3}$ (1.14)

and

$\displaystyle \sigma=ne\mu$ (1.15)

where, $ k_{\mathrm{B}}$ is the Boltzmann constant, $ h$ the Planck constant, $ e$ the elementary charge, $ m^*$ the effective mass, and $ \mu$ the carrier mobility. In addition, the Wiedemann-Franz law relates the thermal conductivity of charge carriers to the electrical conductivity by:

$\displaystyle \kappa_e=L\sigma T$ (1.16)

where $ L$ is the Lorenz number:

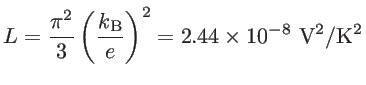$\displaystyle L=\frac{\pi^2}{3}\left( \frac{k_{\mathrm{B}}}{e} \right)^2=2.44 \times 10^{-8}~\mathrm{V^2/K^2}$ (1.17)

The electrical conductivity is proportional to the carrier concentration, whereas the Seebeck coefficient is inversely proportional to the carrier concentration. Therefore, if one tries to increase $ ZT$ by increasing $ n$ and thus $ \sigma$ , one may lose the gain through the reduction of $ S$ (and increase in $ \kappa_e$ ). Figure 1.6 schematically shows that insulators have high Seebeck coefficient and extremely low electrical conductivity, whereas metals have high electrical conductivity and a low Seebeck coefficient [7]. Therefore, in semiconducting materials a finite maximum of the thermoelectric power factor is achieved. As a result, the most effective way to enhance the thermoelectric figure of merit of bulk materials is to decrease the lattice contribution to the thermal conductivity $ \kappa_l$ . However, thermal conductivity reduction, without decreasing the power factor, was not possible for a long time (in all efforts up to the 1990s), and the $ ZT$ values were limited to unity. This translates to low conversion efficiencies and limited applications for thermoelectricity.

Figure 1.6: Variation of the transport coefficients as a function of the carrier concentration.
Image ISM

next up previous contents
Next: 1.4 Nanostructured Materials for Thermoelectrics Up: 1. Introduction Previous: 1.2 Device Efficiency   Contents
H. Karamitaheri: Thermal and Thermoelectric Properties of Nanostructures