Bismuth and its compounds that are commonly used in thermoelectric applications [5] suffer from high cost. In addition, tellurium compounds cannot be used in large-scale applications due to rarity. Silicon, on the other hand, is the second most abundant element on earth and has been used in large scale manufacturing processes. Silicon is the most widely used material in semiconductor industry and its fabrication process are optimized. Silicon crystallizes in a diamond structure with lattice constant of
![]() (see Fig. 1.9) and has a bandgap of nearly
(see Fig. 1.9) and has a bandgap of nearly
![]() and thermal conductivity of
and thermal conductivity of
![]() at room temperature. Due to high thermal conductivity at room temperature bulk silicon has
at room temperature. Due to high thermal conductivity at room temperature bulk silicon has
![]() , which makes it a very
poor thermoelectric. However, recent experimental studies showed that the thermal
conductivity is sharply reduced in silicon-based nanostructures, i.e. nanowires and thin
layers [17,20,21]. The large reduction in the thermal conductivity was attributed to enhanced scattering of phonons on the surfaces of the nanochannels. As a result,
, which makes it a very
poor thermoelectric. However, recent experimental studies showed that the thermal
conductivity is sharply reduced in silicon-based nanostructures, i.e. nanowires and thin
layers [17,20,21]. The large reduction in the thermal conductivity was attributed to enhanced scattering of phonons on the surfaces of the nanochannels. As a result, ![]() values of about
values of about ![]() were achieved at room temperature, a large improvement compared to
were achieved at room temperature, a large improvement compared to ![]() of bulk silicon. Furthermore, it should be possible to reach even higher values of
of bulk silicon. Furthermore, it should be possible to reach even higher values of ![]() using techniques for optimizing the geometry, transport and confinement orientations, and confinement size.
using techniques for optimizing the geometry, transport and confinement orientations, and confinement size.
On the other hand, graphene, a recently discovered form of carbon, has received much
attention over the past few years due to its excellent electrical, optical, and thermal
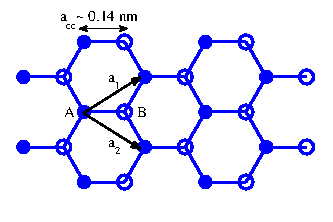
properties [22]. As shown in Fig. 1.10, carbon atoms in graphene are tightly packed into a two-dimensional (2D) honeycomb lattice due to their
![]() hybridization. The primitive unit cell is defined by two lattice vectors
hybridization. The primitive unit cell is defined by two lattice vectors ![]() and
and ![]() :
:
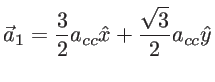 |
(1.18) |
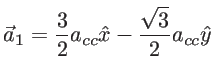 |
(1.19) |
|