2.2.1 Electronic Structure

As proposed by Slater in 1954, the bandstructure of silicon (as well as that of other diamond-like semiconductors) can be calculated using the $sp^3$ tight-binding method. This method considers four valence orbitals $3s$ and $3p^3$ , including $3p_x$ , $3p_y$ , and $3p_z$ , for each silicon atom [31]. To enhance accuracy for reproducing the conduction band of diamond and zinc blende semiconductors, it is common to use the $sp^3s^*$ tight-binding method in which the first excited $s$ -like orbital $s^*$ (i.e. $4s$ in the case of silicon) is also included [46]. It was further improved by including the five excited $d$ orbitals $4d^5$ in the so called $sp^3d^5s^*$ tight-binding method. This method includes ten orbitals per silicon atom.

We first consider the $sp^3d^5s^*$ tight-binding method without spin-orbit coupling for bulk silicon, the unitcell of which consists of two atoms commonly called the anion and the cation. Each anion atom is connected to four cation atoms through for bonds $B_1$ , $B_2$ , $B_3$ , and $B_4$ and vice versa. The Hamiltonian of the unitcell, when considering the coupling of the anion with only one neighboring cation, consists of four blocks as:

$$H= \left[ \begin{array}{ll} H_{aa} & H_{ac} \\ H_{ca} & H_{cc} \\ \end{array} \right]$$ (2.13)

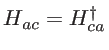Here, $H_{aa}$ and $H_{cc}$ represent the on-site terms and $H_{ac}=H_{ca}^{\dagger}$ the coupling between two atoms. In the case of silicon, we note that $H_{aa}=H_{cc}$ as the unitcell consists of two similar silicon atoms. The on-site term is a diagonal matrix:

$$H_{aa}=[E_{i,j} \delta_{i,j}]$$ (2.14)

and the coupling term has the form of:

$$H_{ac}=[g_{i,j}^B V_{i,j}^{ac}]$$ (2.15)

where $i$ and $j$ run over all 10 orbital indexes:

$$s,p_x,p_y,p_z,d_{xy},d_{yz},d_{zx},d_{x^2-y^2},d_{z^2-r^2}$$ (2.16)

The $g_{i,j}^B$ in Eq. 2.15 are taken from a sign matrix [47] and depend on the corresponding bond ($B$ ) between the anion and the cation. The matrix elements $V_{i,j}^{ac}$ are formed as

$$V_{i,j}^{ac}=f_{i,j}(l,m,n)V_{u,v}$$ (2.17)

where $f_{i,j}(l,m,n)$ are the two center Slater-Koster energy integrals [31]. $V_{u,v}$ and $E_{i,j}$ are fitting parameters used to correctly capture the details of bandstructure over the entire Brillouin zone. Values are provided in Ref. [44] for silicon.

To describe the top of the valence band correctly, one needs to include the spin-orbit coupling [32]. In this case, the number of orbitals per atom increases to 20 [44,47]. However, the spin-orbit interactions affect only orbitals with different spins of the same atom. Therefore, they are only added to the diagonal blocks $H_{aa}$ , and $H_{cc}$ of the Hamiltonian [47].