3.1.1.1 Electronic Properties

Figure 3.2: The ballistic electronic transmission function as a function of energy with the ribbon's width as a parameter. $m$ varies between 2, 5, 8, and 16 which are corresponding to the ribbon's width of 1, 2, 3, and $6~\mathrm{nm}$ , respectively. $\Delta E$ is the energy difference between first and second conduction band edges.

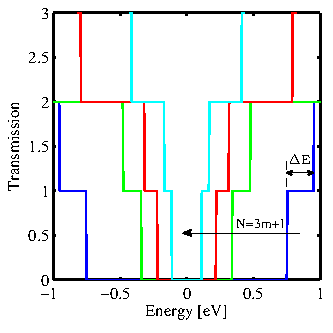
The ballistic transmission function of AGNRs with different widths is shown in Fig. 3.2. As expected, the energy-gap between conduction and valence band decreases with increasing the ribbon's width. Here, we also denote the energy difference between the second and the first conduction subband by $\Delta E$ . This parameter indicates the possibility of a contribution of the second subband to the electronic transport. $E_g$ and $\Delta E$ decrease by increasing the ribbons' width. On the other hand, the derivative of the Fermi function, known as the thermal broadening function, has a width of a few $k_{\mathrm{B}}T$ around $E_{\mathrm{F}}$ . Therefore, the width of the thermal broadening function increases with the temperature and, at high temperature, one can expect the second subband also contribute to the electronic conductance of a wide AGNRs.

Figure 3.3: (a)-(d) show the ballistic electrical transport parameters of a 25-AGNR as a function of $E_c-E_{\mathrm{F}}$ . $E_c$ is the band edge of the first conduction subband. Three different temperatures $150$ , $300$ , and $500~\mathrm{K}$ are considered. (e)-(f) show the transport parameters at the Fermi energy at which the thermoelectric power factor has a maximum (see Fig. 3.3-c).

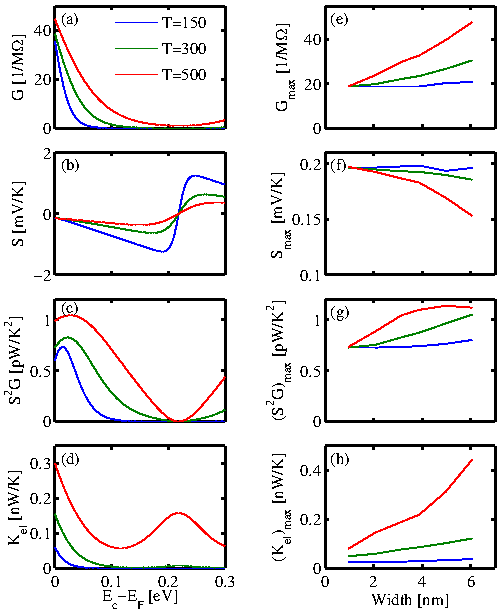
The electrical conductance (Eq. 2.29), the Seebeck coefficient (Eq. 2.37), the thermoelectric power factor ($S^2G$ ), and the electrical contribution to the thermal conductance (Eq. 2.36) of a 25-AGNR as a function of Fermi energy are shown in Fig. 3.3a-d, respectively. Three different temperatures $T=150~\mathrm{K}$ , $300~\mathrm{K}$ , and $500~\mathrm{K}$ are considered. Here, $E_c=E_g/2$ refers to the energy corresponding to the band-edge of the first conduction subband. In contrast to the Seebeck coefficient, the electrical conductance decreases by increasing $E_c-E_{\mathrm{F}}$ , so that the power factor has a maximum near the conduction band-edge. The maximum value of the power factor increases with temperature due to the contribution of the second conduction subband. Different parameters, corresponding to the Fermi energy at which the power factor is maximum, are shown in Fig. 3.3e-f. By increasing the ribbon's width and so decreasing $\Delta E$ , the second conduction band-edge gets closer to the first conduction band-edge $E_c$ . As a result, the overall tranmission function increases near the appropriate Fermi energy, and so the conductance increases with the ribbon's width. This increase is significant at high temperature. On the other hand, the band-gap and so the Seebeck coefficient decrease by increasing $W$ . It is due to the fact that in a low band-gap material, the current of holes and electrons cancel each other out. Overall, the power factor slightly increases by the ribbon's width and temperature. In addition, the electrical contribution to the thermal conductance increases with the ribbon's width and temperature, as well. However, as shown below, it can be neglected in comparison with the lattice thermal conductance.