As shown in Sec. 3.1.1, the high lattice thermal conductance of AGNRs causes a small ballistic ![]() value. In fact, A high thermal conductivity in the range of
value. In fact, A high thermal conductivity in the range of
![]() has been reported for wide suspended single-layer
graphene [28,72], which is only weakly affected by the
boundary and substrate scatterings. On the other hand, in narrow AGNRs, line-edge-roughness (LER) is the dominant scattering source for both electron and phonon transport [73,74,70,75]. Therefore, in this section, we examine how LER scattering in very narrow AGNRs can affect the thermal and thermoelectric properties.
has been reported for wide suspended single-layer
graphene [28,72], which is only weakly affected by the
boundary and substrate scatterings. On the other hand, in narrow AGNRs, line-edge-roughness (LER) is the dominant scattering source for both electron and phonon transport [73,74,70,75]. Therefore, in this section, we examine how LER scattering in very narrow AGNRs can affect the thermal and thermoelectric properties.
|
Very recently, the effect of rough boundaries has been studied in defective AGNRs [76,77,70,78,79,80]. Those previous works have used a simple model for line-edge-roughness which neglect the correlation of the roughness. However, due to the wave nature of phonos, the correlation length of roughness plays an important role as well. To model LER-limited thermal conductivity, an exponential autocorrelation function is employed [81]:
To investigate the effect of LER on the thermal conductivity and the
MFP of phonons, we performed simulations on a statistical sample of 16-AGNR with
roughness parameters of
![]() and
and
![]() . The main results are, however, almost independent of the actual value of the roughness parameters. The statistical average of the transmission function
is shown in Fig. 3.7 for a channel length of
. The main results are, however, almost independent of the actual value of the roughness parameters. The statistical average of the transmission function
is shown in Fig. 3.7 for a channel length of
![]() . For reference, the ballistic
transmission of a 16-AGNR is also shown with solid line.
. For reference, the ballistic
transmission of a 16-AGNR is also shown with solid line.
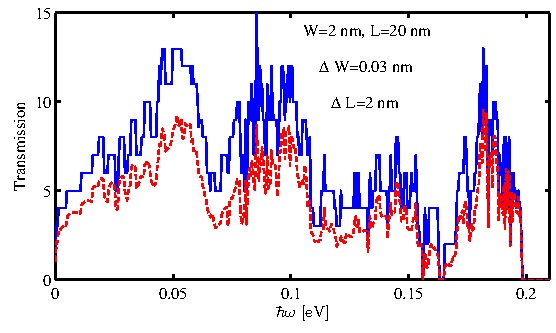
Figure 3.7 compares the phonon transmission functions of a 16-AGNR
assuming perfect edges and rough edges with roughness parameters of
![]() and
and
![]() nm. By introducing LER, the tranmission decreases from the ballistic value almost over entire energy range. To quantify the dependence of the transmission function on the channel length, the phonon MFP
is defined as [32,57]:
nm. By introducing LER, the tranmission decreases from the ballistic value almost over entire energy range. To quantify the dependence of the transmission function on the channel length, the phonon MFP
is defined as [32,57]:
|
|
|
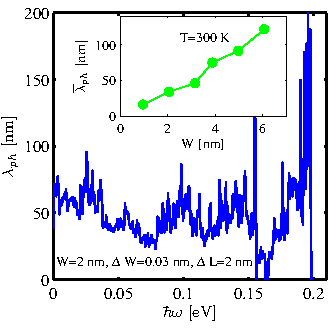
Figure. 3.8 shows the phonon MFP of a 16-AGNR as a function of phonon frequency, which is around
![]() . However, to study the dependence of the
thermal conductance on the channel length one can define an effective
MFP
. However, to study the dependence of the
thermal conductance on the channel length one can define an effective
MFP
![]() as [19]:
as [19]:
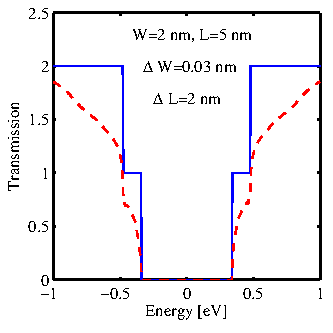
To examine the effect of LER on the electronic structure, the
electronic transmission of a 16-AGNR with the channel length of
![]() is shown in Fig. 3.9, with and without
the LER. LER degrades the transport of electrons at
different energies. However, the reduction is lower at energies near
the sub-band edges, where the density of states and thus the scattering rate
is higher. Therefore, the presence of LER degrades the sharp features
of electronic transmission function and the thermoelectric power
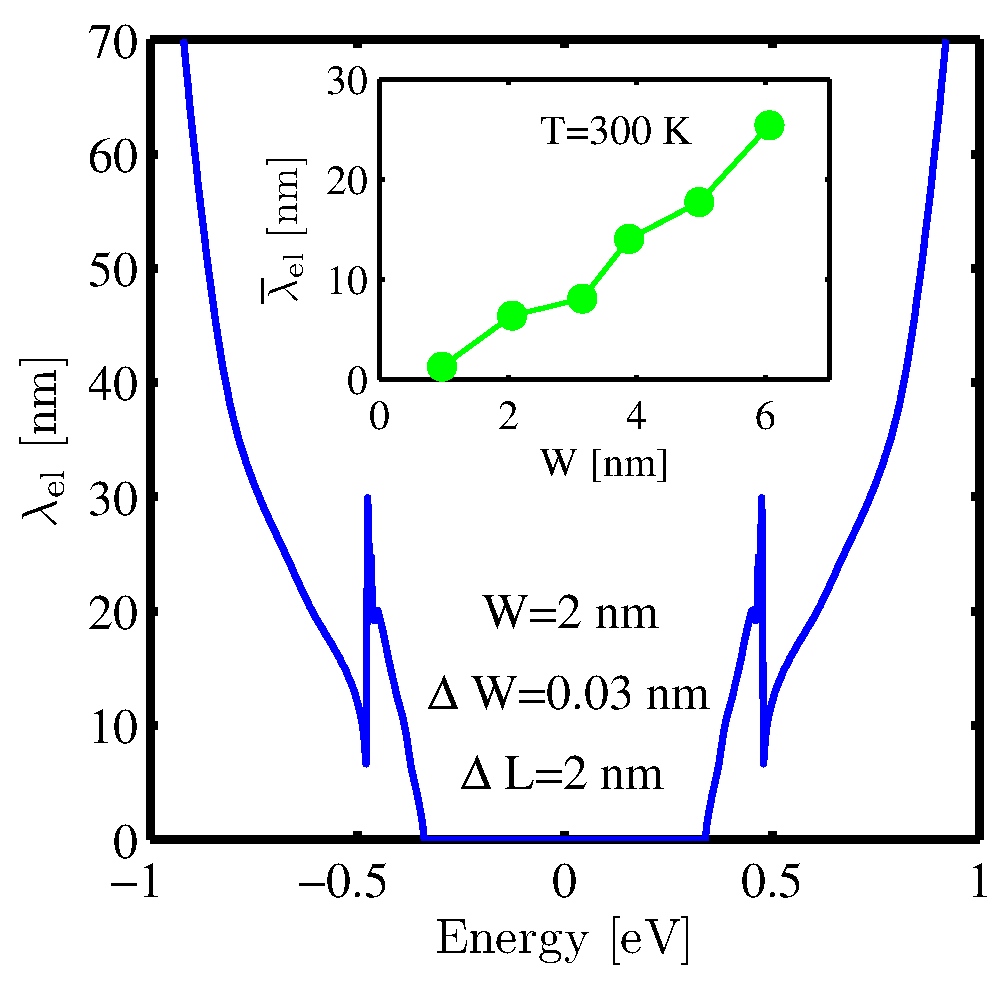
factor [83]. The corresponding MFP is shown in
Fig. 3.10. The MFP is very small near the band edges due to
the high density of states and thus high scattering rate. This indicates that the
diffusive transmission function is very negligible near the first
conduction subband (Fermi energy), which can drastically degrade the
transport parameters. The effective MFP is also shown in the inset of
Fig. 3.10. It increases almost nearly with the ribbon's
width. However it is smaller than
is shown in Fig. 3.9, with and without
the LER. LER degrades the transport of electrons at
different energies. However, the reduction is lower at energies near
the sub-band edges, where the density of states and thus the scattering rate
is higher. Therefore, the presence of LER degrades the sharp features
of electronic transmission function and the thermoelectric power
factor [83]. The corresponding MFP is shown in
Fig. 3.10. The MFP is very small near the band edges due to
the high density of states and thus high scattering rate. This indicates that the
diffusive transmission function is very negligible near the first
conduction subband (Fermi energy), which can drastically degrade the
transport parameters. The effective MFP is also shown in the inset of
Fig. 3.10. It increases almost nearly with the ribbon's
width. However it is smaller than
![]() even for
even for
![]() AGNR. The small electron MFP can be described by considering the sensitivity of the band-gap to the ribbons width. The band-gap is not only inversely dependent on the ribbon's width, it is strongly dependent to the index of the ribbon either. Therefore, the presence of LER is not a small perturbation for the electron transport. In fact, the electron transmission will be in the localization regime and one should even define the localization length instead of mean-free-path for long channel [74]. As the ratio
AGNR. The small electron MFP can be described by considering the sensitivity of the band-gap to the ribbons width. The band-gap is not only inversely dependent on the ribbon's width, it is strongly dependent to the index of the ribbon either. Therefore, the presence of LER is not a small perturbation for the electron transport. In fact, the electron transmission will be in the localization regime and one should even define the localization length instead of mean-free-path for long channel [74]. As the ratio
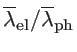 is
considerably smaller than one, we conclude that the presence of boundary
scattering is not appropriate for the thermoelectric performance of
AGNR-based devices, in contrast to what has been observed in silicon nanowires [20].
is
considerably smaller than one, we conclude that the presence of boundary
scattering is not appropriate for the thermoelectric performance of
AGNR-based devices, in contrast to what has been observed in silicon nanowires [20].
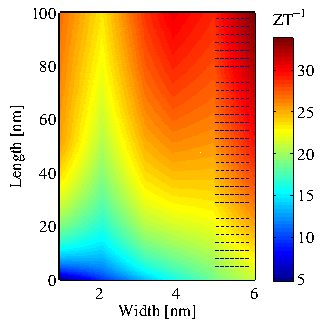
Finally, the inverse of ![]() at room temperature as a function of ribbon's width and channel
length is shown in Fig. 3.11. For very short channels, in which the transport is almost
ballistic, the value of
at room temperature as a function of ribbon's width and channel
length is shown in Fig. 3.11. For very short channels, in which the transport is almost
ballistic, the value of ![]() is
is ![]() for narrow ribbons and it
decreases by increasing the width, as described in
Sec. 3.1.1. However, the value of
for narrow ribbons and it
decreases by increasing the width, as described in
Sec. 3.1.1. However, the value of ![]() decreases by
increasing the channel length, as the electron tranmission decreases
faster than the phonon transmission function. For the channel length
of about
decreases by
increasing the channel length, as the electron tranmission decreases
faster than the phonon transmission function. For the channel length
of about
![]() ,
, ![]() is less than
is less than ![]() , and even smaller values are expected for longer ribbons.
, and even smaller values are expected for longer ribbons.
|
In this section, the ballistic and diffusive thermoelectric properties of narrow AGNRs
are comprehensively studied. The results indicate that the
contribution of the second conduction subband increases the power
factor. The second conduction is closer to the first one in wider ribbons. However, the small band-gap of wide AGNRs
degrades the Seebeck coefficient. Designing an AGNR with large
band-gap and closer conduction subbands is the way that could
significantly improve the thermoelectric power factor. On the other
hand, the high thermal conductance degrades the thermoelectric
performance of AGNRs. Using line-edge-roughness for decreasing the
thermal conductance degrades the thermoelectric properties, as it is more severe in the case of electron transport. Engineering AGNR-based materials in which the transport of phonons is more sensitive to the boundary scatting than that
of electrons can help to improve or at leat retain the ![]() values in
long ribbons. It might be accessible in some structures, in which the
band-gap is not strongly related to the width. In the next couple of sections, these ideas are used in order to achieve high performance graphene-based thermoelectric devices.
values in
long ribbons. It might be accessible in some structures, in which the
band-gap is not strongly related to the width. In the next couple of sections, these ideas are used in order to achieve high performance graphene-based thermoelectric devices.