3.3.1 The Role of Extended Line Defects

An efficient thermoelectric material must be able to effectively separate hot from cold carriers. The quantity that determines the ability to filter carriers is the Seebeck coefficient. The Seebeck coefficient depends on the asymmetry of the density of states around the Fermi level. In semiconductors the Seebeck coefficient is large, whereas in a metal the density of states is more uniform in energy and the Seebeck coefficient is small. Metallic ZGNRs also have a small Seebeck coefficient because their transmission is constant around the Fermi level, despite the peak in the DOS at $E=0~\mathrm{eV}$ due to the edge states. Recently, however, Bahamon et al. have investigated the electrical properties of ZGNRs that included an ELD (ELD-ZGNRs) along the nanoribbon's length [89]. It was reported that the ELD breaks the electron-hole energy symmetry in nanoribbons, and introduces an additional electron band around the Fermi level. In such a way an asymmetry in the density of states and the transmission function are achieved which improves the Seebeck coefficient. This particular structure has also been experimentally realized recently [90].

For the electronic structure calculations, the Hamiltonian of the GNRs is described in the standard first nearest-neighbor atomistic tight-binding $p_z$ orbital approximation. The hopping parameter is set to $-2.7~\mathrm{eV}$ and the on site potential is shifted to zero so that the Fermi level remains at $0~\mathrm{eV}$ . This model has been recently used to describe the electronic transport of ELD-ZGNR with double-vacancies and the results are in good agreement with first-principle calculations and experimental studies [89,90]. To date, only a few first-principle calculations and experimental studies have been conducted for structures that include ELDs [91,92,90]. The two main features of the electronic structure, the asymmetry between electrons and holes, and the metallic behavior of the ELD in the graphene ribbon have been described in these studies, and are also captured by the tight-binding model, which is used here for ZGNR-based structures.

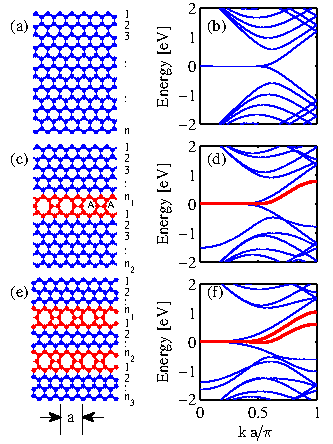
The changes in the electronic structure of the ZGNRs after the introduction of the ELD are demonstrated in Fig. 3.19. Figure 3.19-a shows the atomistic geometry of the pristine ZGNR of width $W\sim 4~\mathrm{nm}$ (with 20 zigzag edge lines) and Fig. 3.19-b its electronic structure. The Fermi level is at $E=0~\mathrm{eV}$ due to the symmetry of the electron and hole bands. Figure 3.19-c shows the structure of the ELD-ZGNR with the same width. The region where the ELD is introduced is shown in red color. The ELD changes the hexagons of the GNR to pentagons and octagons after a local rearrangement of the bonding and the introduction of two additional atoms in the unit cell. To describe the ELD-ZGNR structure a two parameter notation is used as ELD-ZGNR($n_1$ ,$n_2$ ), where $n_1$ and $n_2$ are the indices of the partial-ZGNRs above and below the line defect, respectively (i.e. the number of zigzag edge lines of atoms). In this work we only consider the cases $n_1=n_2$ .

Figure 3.19: The geometrical structure of (a) ZGNR(n), (c) ELD-ZGNR($n_1$ ,$n_2$ ), and (e) 2ELD-ZGNR($n_1$ ,$n_2$ ,$n_3$ ). The bandstructure of (b) ZGNR(20), (d) ELD-ZGNR(10,10), and (f) 2ELD-ZGNR(8,4,8). The bandstructure of ZGNR(20) is folded for a better comparison. The translation vector length is $a=0.49~\mathrm{nm}$ . The numbers $n$ , $n_1$ , $n_2$ and $n_3$ indicate the number of zigzag edges on the top, bottom, and middle of the ELD regions.

The bandstructure of the ELD-ZGNR(10,10) is shown in Fig. 3.19-d. The thick-red line shows a new band that is introduced in the conduction band near the Fermi energy ( $E=0~\mathrm{eV}$ ), which corresponds to the ELD. There are two effects that result in the creation of the extra band. Part of the physics behind this is explained by Pereira et al. in Ref. [93]. The first effect is that a defect in the graphene system will introduce states that reside close to the Fermi level at $E=0~\mathrm{eV}$ . This is similar to the edge states of the ribbons that tend to reside near the Fermi level. The second effect again described in Ref. [93], is that an asymmetry in the dispersion between electrons and holes will be created when carbon atoms of the graphene sublattice A (or B) are coupled with atoms from A (or B) again. Usually, the atomic arrangement in graphene can be splitted in sublattices A and B, where atoms from A couple to B and vise versa. When this happens, the dispersion is symmetric in the first-nearest neighbor tight-binding model. At a defect site such as the ELD, where A connects to A as seen in Fig. 3.19-c, such asymmetry can be observed. The fact that the overall bandstructure has additional bands compared to the pristine ribbon is also caused by the two extra atoms in the unit cell.

Moving one step further, in Fig. 3.19-e the geometry of a GNR with two ELDs is shown. This structure is denoted as 2ELD-ZGNR($n_1$ ,$n_2$ ,$n_3$ ), where $n_1$ , $n_2$ , and $n_3$ denote the the number of zigzag carbon lines above, within, and below the line defects. Figure 3.19-f shows the electronic structure of the 2ELD-ZGNR(8,4,8). In this case two additional bands are introduced near the Fermi level as designated by the thick-red lines. In this structure the asymmetry between electron and hole bands around the Fermi level ( $E=0~\mathrm{eV}$ ) is further enhanced.

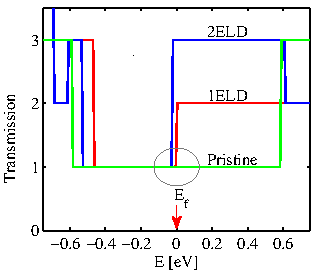
Figure 3.20 demonstrates the increase in the asymmetry of the bands around the Fermi level by showing how the transmission changes when one or two ELDs are introduced in the channel. For the pristine ZGNR, the transmission is equal to one, indicating the existence of a single propagating band at energies around the Fermi level (green line). With the introduction of one ELD, the conduction band ( $E>0~\mathrm{eV}$ ) is composed of two subbands, whereas the valence band ( $E<0~\mathrm{eV}$ ) is still composed of one subband. With the introduction of two ELDs, three conduction subbands appear, but still only one valence subband. As it will be shown below, this asymmetry will improve the Seebeck coefficient. This constitutes the first design step in improving the thermoelectric performance of ZGNRs.

Figure 3.20: The transmission function for three different structures: i) The pristine ZGNR(20), ii) ELD-ZGNR(10,10), and iii) 2ELD-ZGNR(8,4,8).

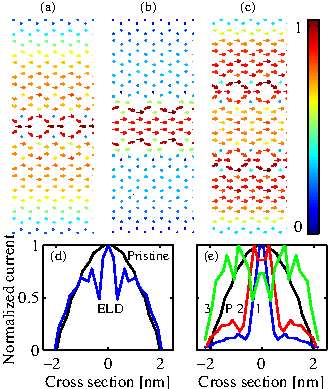
There is, however, another point worth mentioning. In Fig. 3.21 the colormaps show the normalized current spectrum at $E=0.2~\mathrm {eV}$ in the cross sections of the ELD-ZGNRs described in Fig. 3.20. Figure 3.21-a shows the current spectrum of the ELD-ZGNR(10,10). The current is zero close to the edges of the ribbon and peaks near the center. This is demonstrated more clearly in Fig. 3.21-d, which shows the current along one atomic chain perpendicular to this channel (blue line). The black line of Fig. 3.21-d illustrates the current density on the cross section of the pristine ZGNR channel for reference.

Figure 3.21: Normalized current spectrum at $E=0.2~\mathrm {eV}$ for (a) ELD-ZGNR(10,10), (b) 2ELD-ZGNR(8,4,8), and (c) 2ELD(7,6,7). (d) The current in the cross section of ZGNR(20) (black line) and ELD-ZGNR(10,10) (blue line). (e) The current in the cross section of ZGNR(20) (black line), 2ELD-ZGNR(9,2,9) (blue line), 2ELD-ZGNR(8,4,8) (red line), and 2ELD-ZGNR(7,6,7) (green line).

The current spectrum for the 2ELD-ZGNR(8,4,8) is shown in Fig. 3.21-b. The situation is now different since most of the current is confined within the two ELDs. This, however, is the case only when the distance between the ELDs is smaller than the widths of the upper/lower regions. In the case where the width of the middle region is similar to the widths of the upper/lower regions, the current is spread more uniformly in the channel as shown in Fig. 3.21-c for the 2ELD-ZGNR(7,6,7) channel. Figure 3.21-e shows again the current along one atomic chain in the cross section of these ribbons. The current spectrum is localized in the middle of the channel in the 2ELD-ZGNR(8,4,8) channel (red line) compared to the pristine channel (black line). In a 2ELD-ZGNR(9,2,9) channel with a narrower middle region the current spectrum is localized even closer around the center (blue line). A large portion of the current is in general flowing around the ELD regions. The design capability to localize the current spectrum in the middle of the channel away from the edges will prove advantageous in the presence of edge roughness since the current in this case will be less affected. On the other hand, in the case of the 2ELD-ZGNR(7,6,7) channel the current spectrum tends to concentrate more close to the edges (green line).