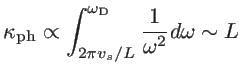


Next: 5.3 The Effect of Phonon-Phonon Scattering
Up: 5.2 The Long-Wavelength Problem
Previous: 5.2 The Long-Wavelength Problem
Contents
In this work, the thermal conductivity in the silicon nanowires is calculated using the phonon lifetime approximation in the phononic Boltzmann transport equation (Eq. 2.72). For the calculation of the relaxation times, we adopt the bulk formalism for Umklapp scattering [118,119,57]:
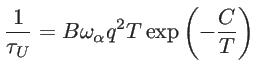 |
(5.1) |
where
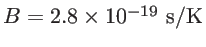 and
and
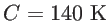 [57]. For boundary scattering we use:
[57]. For boundary scattering we use:
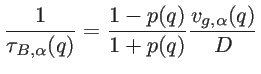 |
(5.2) |
where 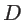 is nanowire diameter and
is nanowire diameter and 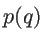 is
is 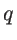 -dependent specularity parameter given by [61,60,112]:
-dependent specularity parameter given by [61,60,112]:
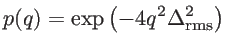 |
(5.3) |
where we used
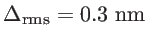 for the root-mean-square of the roughness amplitude. The specularity parameter
for the root-mean-square of the roughness amplitude. The specularity parameter 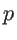 taking values from 0 to 1, is determined by the details of the surface and surface roughness. For a smooth surface
taking values from 0 to 1, is determined by the details of the surface and surface roughness. For a smooth surface 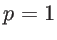 , and the phonon-boundary scattering is fully specular. For a very rough surface
, and the phonon-boundary scattering is fully specular. For a very rough surface 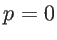 , which results in fully diffusive boundary scattering. Recently, studies showed that
experimental results for boundary scattering in nanowires of diameters
, which results in fully diffusive boundary scattering. Recently, studies showed that
experimental results for boundary scattering in nanowires of diameters
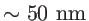 are only explained if an almost fully diffusive boundary is assumed [131,132]. The overall relaxation rate including all scattering mechanisms is computed using Matthiessen's rule.
are only explained if an almost fully diffusive boundary is assumed [131,132]. The overall relaxation rate including all scattering mechanisms is computed using Matthiessen's rule.
When considering the classical description of the energy distribution of phonons,
in the Debye approximation, the heat conductivity of acoustic modes is given by [61,121]:
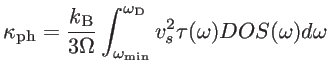 |
(5.4) |
where 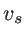 is the corresponding sound velocity,
is the corresponding sound velocity,
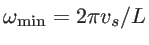 is the minimum allowed phonon frequency which is determined by the longest allowed wavelength at a given channel length, and
is the minimum allowed phonon frequency which is determined by the longest allowed wavelength at a given channel length, and
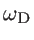 is the Debye frequency. As the bulk density-of-states
is the Debye frequency. As the bulk density-of-states
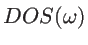 is proportional to
is proportional to 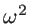 , the Umklapp-limited thermal conductivity in 3D (with
, the Umklapp-limited thermal conductivity in 3D (with
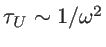 as shown in Eq. 5.1) is bounded, even when the contribution of the long MFP phonons (as
as shown in Eq. 5.1) is bounded, even when the contribution of the long MFP phonons (as
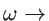 ) is included:
) is included:
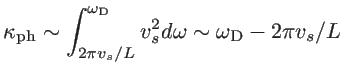 |
(5.5) |
since the second term of Eq. 5.5 goes to zero as the length increases.
In the case of 1D structures, on the other hand, the DOS is finite for low
frequencies
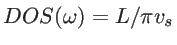 [53], which does not allow the cancellation of the
[53], which does not allow the cancellation of the
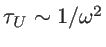 term. Therefore, the Umklapp-limited thermal conductivity of a 1D system is given by:
term. Therefore, the Umklapp-limited thermal conductivity of a 1D system is given by:
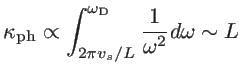 |
(5.6) |
indicating a linear divergence with the channel length. Physically, this means that the lowest wavevector that contributes to thermal conductivity is determined by the length of the channel. For an infinite channel, longer and longer wavevectors of finite DOS are involved, which causes divergence in the thermal conductivity, in contrast to bulk. Several works in the literature attempt to add corrections that would bound
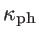 as the
channel length increases [120,126], although large
as the
channel length increases [120,126], although large
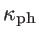 could still be possible in 1D. Some authors still use the bulk dispersion even for ultra-narrow channels [112,133,134], others include a constant specularity parameter for surface roughness, that adds a constant term in the total scattering rate, and removes the singularity for
could still be possible in 1D. Some authors still use the bulk dispersion even for ultra-narrow channels [112,133,134], others include a constant specularity parameter for surface roughness, that adds a constant term in the total scattering rate, and removes the singularity for
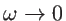 [123,135,101,136]. A different approach was proposed recently by Mingo et al., where an additional rate of a second order 3-phonon scattering mechanism without
[123,135,101,136]. A different approach was proposed recently by Mingo et al., where an additional rate of a second order 3-phonon scattering mechanism without 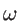 -dependence was introduced for thermal transport in carbon nanotubes as [120]:
-dependence was introduced for thermal transport in carbon nanotubes as [120]:
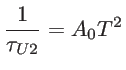 |
(5.7) |
Here 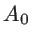 is a frequency independent constant. This is just an order of magnitude approximation which removes the singularity for low frequency phonons, although very high thermal conductivities are still achieved. A study of the exact solution of the phonon BTE in carbon nanotubes showed a saturation in
is a frequency independent constant. This is just an order of magnitude approximation which removes the singularity for low frequency phonons, although very high thermal conductivities are still achieved. A study of the exact solution of the phonon BTE in carbon nanotubes showed a saturation in
 as the length increased to the millimeter range [126], which could prove the suitability of using Eq. 5.7.
as the length increased to the millimeter range [126], which could prove the suitability of using Eq. 5.7.



Next: 5.3 The Effect of Phonon-Phonon Scattering
Up: 5.2 The Long-Wavelength Problem
Previous: 5.2 The Long-Wavelength Problem
Contents
H. Karamitaheri: Thermal and Thermoelectric Properties of Nanostructures
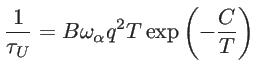
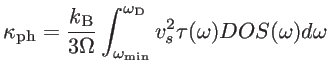
![]() [53], which does not allow the cancellation of the
[53], which does not allow the cancellation of the
![]() term. Therefore, the Umklapp-limited thermal conductivity of a 1D system is given by:
term. Therefore, the Umklapp-limited thermal conductivity of a 1D system is given by: