2.3 Empirical Model Building





Next: 2.3.1 Run Matrix Generation
Up: 2 Mathematical Considerations
Previous: 2.2.2 Sequential Quadratic Programming
Often it is desirable to generate simple polynomial expressions that will approximate TCAD models at a given
input, over a limited region in the parameter space. The polynomial
expressions are typically several orders of magnitude faster than the
model equations. They are used in lieu of the original TCAD model in
applications where computational efficiency and/or continuity requirements
are critical. For instance, their substitute role in Monte Carlo analysis to
simulate statistical manufacturing variation is well
documented [95][65][37].
that will approximate TCAD models at a given
input, over a limited region in the parameter space. The polynomial
expressions are typically several orders of magnitude faster than the
model equations. They are used in lieu of the original TCAD model in
applications where computational efficiency and/or continuity requirements
are critical. For instance, their substitute role in Monte Carlo analysis to
simulate statistical manufacturing variation is well
documented [95][65][37].
The new set of equations can be written as a standard model with no input
variables. Furthermore, the task of generating the approximating polynomial
for each model output is independent of the other outputs which are
simultaneously calculated during model evaluation. In what follows, the
discussion is restricted to one output:
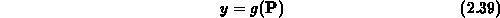
The process is replicated for outputs in a multiple-output TCAD model.
A polynomial function in the parameters 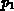 ,
, 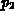 ,
,  ,
,
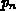 is a linear combination of products of the powers of
is a linear combination of products of the powers of 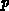 's. It can be
written as:
's. It can be
written as:
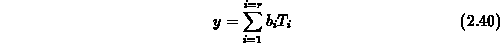
where  is the number of terms in the model,
is the number of terms in the model, 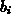 is the constant
coefficient multiplying the
is the constant
coefficient multiplying the 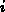 th term
th term 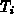 . Each
. Each 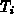 is a product
of powers of
is a product
of powers of 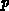 's:
's:
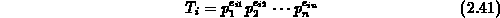
where 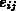 is the exponent of the parameter
is the exponent of the parameter 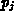 in the
in the 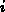 th term
product:
th term
product: 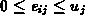 ,
, 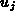 being a small positive number.
The order of the
being a small positive number.
The order of the 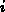 th term,
th term, 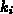 , is calculated by summing the values
of its exponents:
, is calculated by summing the values
of its exponents:
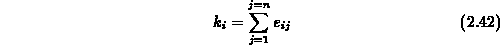
Finally, the degree of a polynomial is equal to the highest order in its terms.
In practice small order (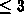 ) polynomials are used. Let:
) polynomials are used. Let:
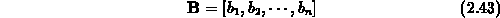
be the vector of coefficients, and
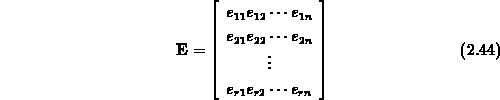
be the matrix of exponents of all terms.
The model building algorithm objective is to determine the number of
terms  and the values of the elements of
and the values of the elements of 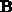 and
and 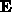 .
The first step consists of identifying the order of dependency between The
model output and each of the model parameters. This can be accomplished
using some initial screening algorithm [95][65][15]
or by user input based on expectation and/or knowledge of the underlying
physical theory. In general, the higher the order of
dependency the more time consuming the building process will be as more model
evaluations are required.
.
The first step consists of identifying the order of dependency between The
model output and each of the model parameters. This can be accomplished
using some initial screening algorithm [95][65][15]
or by user input based on expectation and/or knowledge of the underlying
physical theory. In general, the higher the order of
dependency the more time consuming the building process will be as more model
evaluations are required.
Based on the dependency information an experimental
run matrix is generated. Each row in the run matrix represent one
point in the model parameter space. By evaluating the TCAD model at each
of these points the required fitting data is generated.
The number of terms and the corresponding coefficients are then determined by
polynomial approximation with a minimum number of terms. The experimental
matrix generation and the polynomial approximation are described next.





Next: 2.3.1 Run Matrix Generation
Up: 2 Mathematical Considerations
Previous: 2.2.2 Sequential Quadratic Programming
Martin Stiftinger
Tue Aug 1 19:07:20 MET DST 1995
 that will approximate TCAD models at a given
input, over a limited region in the parameter space. The polynomial
expressions are typically several orders of magnitude faster than the
model equations. They are used in lieu of the original TCAD model in
applications where computational efficiency and/or continuity requirements
are critical. For instance, their substitute role in Monte Carlo analysis to
simulate statistical manufacturing variation is well
documented [95][65][37].
that will approximate TCAD models at a given
input, over a limited region in the parameter space. The polynomial
expressions are typically several orders of magnitude faster than the
model equations. They are used in lieu of the original TCAD model in
applications where computational efficiency and/or continuity requirements
are critical. For instance, their substitute role in Monte Carlo analysis to
simulate statistical manufacturing variation is well
documented [95][65][37].





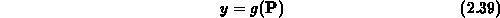
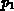 ,
, 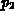 ,
,  ,
,
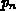 is a linear combination of products of the powers of
is a linear combination of products of the powers of 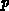 's. It can be
written as:
's. It can be
written as:
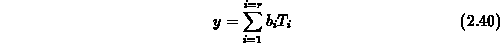
 is the number of terms in the model,
is the number of terms in the model, 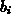 is the constant
coefficient multiplying the
is the constant
coefficient multiplying the 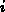 th term
th term 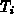 . Each
. Each 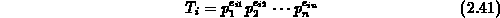
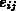 is the exponent of the parameter
is the exponent of the parameter 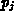 in the
in the 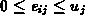 ,
, 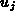 being a small positive number.
The order of the
being a small positive number.
The order of the 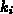 , is calculated by summing the values
of its exponents:
, is calculated by summing the values
of its exponents:
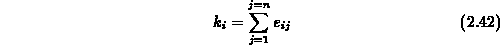
 ) polynomials are used. Let:
) polynomials are used. Let:
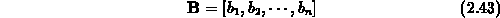
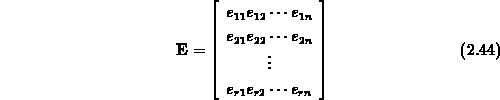
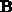 and
and 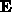 .
The first step consists of identifying the order of dependency between The
model output and each of the model parameters. This can be accomplished
using some initial screening algorithm
.
The first step consists of identifying the order of dependency between The
model output and each of the model parameters. This can be accomplished
using some initial screening algorithm