

 Previous: 8.3 Conservation of Mass
Up: 8.3 Conservation of Mass
Next: 8.3.2 Meshing Constraints
Previous: 8.3 Conservation of Mass
Up: 8.3 Conservation of Mass
Next: 8.3.2 Meshing Constraints
The physical quantity associated with the zeroth order moment
is the carrier density 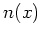 :
The zeroth order moment equation describes the conservation
of particle number, also called conservation of mass.
:
The zeroth order moment equation describes the conservation
of particle number, also called conservation of mass.
We derive the corresponding conservation equation by
integrating the Wigner equation over all velocities
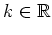
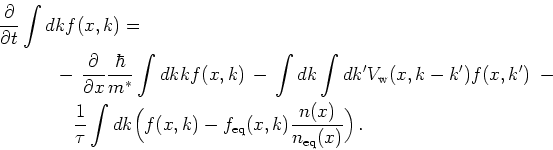 |
(8.6) |
By definition the Wigner potential
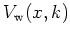 is an odd
function in
is an odd
function in 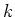 . Hence the contribution from the integral
. Hence the contribution from the integral
vanishes.
This property expresses conservation of particle
number from potential scattering.
In a similar way the term stemming from scattering also vanishes as
we have
With the introduction of the (particle) current density 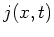 :
:
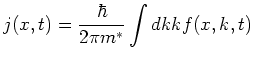 |
(8.8) |
we finally get the continuity equation (in vector notation):
The aim is to find a discretization of the full Wigner equation
which conserves mass.


 Previous: 8.3 Conservation of Mass
Up: 8.3 Conservation of Mass
Next: 8.3.2 Meshing Constraints
Previous: 8.3 Conservation of Mass
Up: 8.3 Conservation of Mass
Next: 8.3.2 Meshing Constraints
R. Kosik: Numerical Challenges on the Road to NanoTCAD
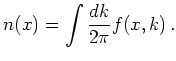
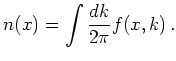
![]()
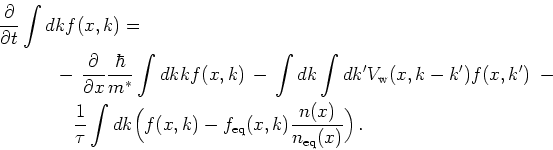
![]() is an odd
function in
is an odd
function in ![]() . Hence the contribution from the integral
. Hence the contribution from the integral
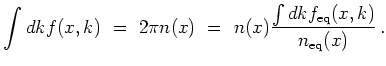
![]() :
:
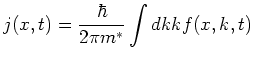
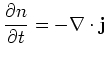
![]()
![]()
![]()
![]() Previous: 8.3 Conservation of Mass
Up: 8.3 Conservation of Mass
Next: 8.3.2 Meshing Constraints
Previous: 8.3 Conservation of Mass
Up: 8.3 Conservation of Mass
Next: 8.3.2 Meshing Constraints