8.4 Discretization

In the previous section we derived meshing constraints necessary for a mass conserving discretization. We discretize now directly the Wigner equation using finite differences on an equispaced product-grid in 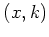$(x,k)$. Alternative approaches discretize the Schrödinger or von Neumann equation and perform some kind of a discrete Wigner transformation. This leads to difficulties with the domain of the mesh, see [Fre87]. See also [MH94] where the Schrödinger equation is carefully discretized and a staggered grid is used. Our implementation follows [Bie97] and [KKFR89]. Some physical background can be found in [Fre90].

For the Wigner equation our main interest was in the stationary case as the Monte Carlo simulator was based on the stationary method. The discretization of the terms for free streaming, potential and relaxation time scattering is largely independent from each other. They are treated separately in the next subsections.