

 Previous: 10.2.1 Coherence Length
Up: 10.2 Discussion of Discrepancy
Next: 10.2.3 Boundary Conditions
Previous: 10.2.1 Coherence Length
Up: 10.2 Discussion of Discrepancy
Next: 10.2.3 Boundary Conditions
The mesh size is critical because of the sharp resonances
in the transmission
probabilities. Figure 10.5 depicts
the transmitted current density over the wave vector 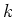 as calculated by the QTBM.
The GaAs/AlGaAs RTD is in equilibrium, particles are injected from
the left and the right with a Fermi-Dirac distribution.
In the example shown the energy corresponding to the highest
as calculated by the QTBM.
The GaAs/AlGaAs RTD is in equilibrium, particles are injected from
the left and the right with a Fermi-Dirac distribution.
In the example shown the energy corresponding to the highest
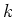 -value is
-value is
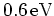 .
.
Figure 10.5:
Spikes in the transmitted current density resulting from
sharp resonances
|
|
For the QTBM the 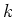 -mesh used for the injected particles
is refined in the region of the resonance.
The necessary resolution in
-mesh used for the injected particles
is refined in the region of the resonance.
The necessary resolution in
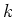 to resolve the resonances is not in the numerically feasible
domain for the finite difference Wigner function method.
The needed number of points in
to resolve the resonances is not in the numerically feasible
domain for the finite difference Wigner function method.
The needed number of points in 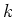 ,
, 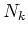 , is
too high and the used equi-spaced mesh does
not resolve the sharp peaks.
In a comparison between WFM and QTBM the problem
is aggravated as also the limit
, is
too high and the used equi-spaced mesh does
not resolve the sharp peaks.
In a comparison between WFM and QTBM the problem
is aggravated as also the limit
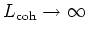 has
to be performed.
has
to be performed.
The used mesh sizes in the Wigner method are too small to ensure
an accurate solution for coherent transport.
The choice of a very crude mesh is
sometimes justified by out of place physical arguments
(``atomic monolayer
spacing'') or even by a reference to the uncertainty relation.
As the finite difference Wigner method is a dense discretization
in 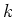 , the mesh sizes which are feasible in practice are only
limited. Much of the work on Wigner simulation was done 10
to 15 years ago and small mesh sizes like this were used.
, the mesh sizes which are feasible in practice are only
limited. Much of the work on Wigner simulation was done 10
to 15 years ago and small mesh sizes like this were used.
In defense of the Wigner method we note that scattering
is usually included in the WFM model.
In this case the transmission peaks are naturally broadened
and meshing constraints are less stringent.


 Previous: 10.2.1 Coherence Length
Up: 10.2 Discussion of Discrepancy
Next: 10.2.3 Boundary Conditions
Previous: 10.2.1 Coherence Length
Up: 10.2 Discussion of Discrepancy
Next: 10.2.3 Boundary Conditions
R. Kosik: Numerical Challenges on the Road to NanoTCAD
![\includegraphics[width=0.9\columnwidth
]{Figures/FigTransCurrDens}](img778.png)
![]() , the mesh sizes which are feasible in practice are only
limited. Much of the work on Wigner simulation was done 10
to 15 years ago and small mesh sizes like this were used.
, the mesh sizes which are feasible in practice are only
limited. Much of the work on Wigner simulation was done 10
to 15 years ago and small mesh sizes like this were used.
![]()
![]()
![]()
![]() Previous: 10.2.1 Coherence Length
Up: 10.2 Discussion of Discrepancy
Next: 10.2.3 Boundary Conditions
Previous: 10.2.1 Coherence Length
Up: 10.2 Discussion of Discrepancy
Next: 10.2.3 Boundary Conditions