previous up next contents Previous: 2.2.3 Closure Problem Up: 2.2 The Method of Next: 2.3 Closure Relations for

2.2.4 Boundary Conditions

We choose the same boundary conditions as are implicitly used in the Monte Carlo simulator. Essentially these consist in Dirichlet boundary conditions for the ``incoming'' part of the distribution, as this corresponds to the injected particles.

We use Dirichlet boundary conditions for the even moments stemming from a ``cold'' Maxwellian distribution. We also assume local charge neutrality at the boundaries, that is, the carrier density $ n$ is equal to the doping $ C$.

The equilibrium values $ \langle \hat{O}_i \rangle_{\mathrm{eq}}$ are a function of the lattice temperature $ T_{\mathrm{L}}$ and for parabolic band we obtain ([Gri02], page 17):

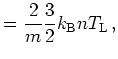$\displaystyle \langle O_2 \rangle_{\mathrm{eq}}$ $\displaystyle = \frac{2}{m} \frac{3}{2} k_{\mathrm{B}} n T_{\mathrm{L}} ,$ (2.49)
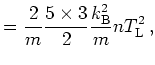$\displaystyle \langle O_4 \rangle_{\mathrm{eq}}$ $\displaystyle = \frac{2}{m} \frac{5 \times 3}{2} \frac{k_{\mathrm{B}}^2}{m}n T_{\mathrm{L}}^2 ,$ (2.50)
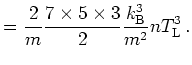$\displaystyle \langle O_6 \rangle_{\mathrm{eq}}$ $\displaystyle = \frac{2}{m} \frac{7 \times 5 \times 3}{2} \frac{k_{\mathrm{B}}^3}{m^2} n T_{\mathrm{L}}^3 .$ (2.51)

previous up next contents Previous: 2.2.3 Closure Problem Up: 2.2 The Method of Next: 2.3 Closure Relations for

R. Kosik: Numerical Challenges on the Road to NanoTCAD