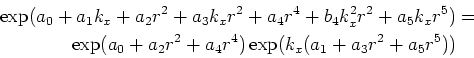 |
(3.11) |
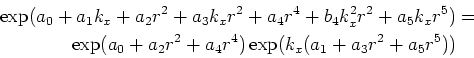 |
(3.11) |
| (3.12) |
which is of the linear-isotropic type. Given
the even moments, the parameters ![]() and
and ![]() can
be determined. However, not for every combination
of
can
be determined. However, not for every combination
of ![]() and
and ![]() from a distribution function
from a distribution function
![]() we can find such parameters. In particular, it
can be shown, that
we can find such parameters. In particular, it
can be shown, that
In Equation 3.13 the value
![]() comes from a Gaussian distribution.
The value of 1 is reached from a distribution function of
the form
comes from a Gaussian distribution.
The value of 1 is reached from a distribution function of
the form
![]() in the limit
in the limit
![]() .
.
Likewise one can show that
must hold. Our implementation of the diffusion closure uses
one lookup table for ![]() and one for
and one for
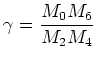 |
(3.16) |
both parameterized by the single parameter
![]() . From the study of
Monte Carlo data we know
that the range of parameters
. From the study of
Monte Carlo data we know
that the range of parameters ![]() and
and ![]() in the results largely exceeds the
range of
in the results largely exceeds the
range of ![]() and
and ![]() given by Equations 3.13 and 3.15.
given by Equations 3.13 and 3.15.
![]()
![]()
![]()
![]() Previous: 3.2.2 Critique and Modifications
Up: 3.2 Maximum Entropy Closure
Next: 3.3 Higher Order Statistics
Previous: 3.2.2 Critique and Modifications
Up: 3.2 Maximum Entropy Closure
Next: 3.3 Higher Order Statistics