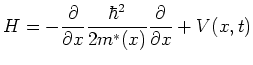7.1.1 Open Quantum Systems

We consider a one-dimensional system described by a simple single-particle Hamiltonian

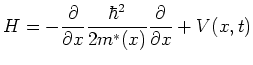$$H = - \frac{\partial}{\partial x} \frac{\hbar^2}{2m^{*}(x)} \frac{\partial}{\partial x} + V(x,t)$$ (7.1)

where $V(x,t)$ denotes the (possibly time-dependent) potential energy of the electron, $m^{*}(x)$ its (possibly space-dependent) effective mass, $\frac{\partial}{\partial x}$ is the one-dimensional spatial derivative (with $-\imath \hbar \partial_x$ representing the momentum operator), and $\hbar$ is the Planck constant.

In applications the simulation domain is usually taken to be finite. The influence of the domain which is cut away on the left and on the right is modeled by imposing special equations for the boundary.

In our applications the boundaries are physically given by device contacts. In this case open boundary conditions have to be employed. The boundary conditions describe the interaction of the system with the environment.

Outgoing particle waves shall leave the device without being reflected at the boundary. The waves appear to be completely absorbed at the boundary - for this reason one also uses the term ``absorbing boundary conditions".

The open boundary conditions change the character of the equation. We get a dissipative Schrödinger operator, time reversibility is lost. Technically this change creates a problem in the interpretation. In standard quantum mechanics only self-adjoint operators present valid observables. However, the self-adjointness of - for instance - the momentum operator on a finite domain depends on the boundary conditions. This is discussed in [KNR02] for the Schrödinger equation using a different type of open boundary conditions. For a discussion of the need for self-adjointness demonstrated by analysis of an elementary textbook example we recommend [BFV01] to the reader.