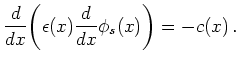 |
(7.17) |
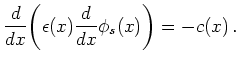 |
(7.17) |
Self-consistency in electronic device simulation means ensuring that the carrier density profile in the simulated device is consistent with its potential profile. The self-consistent field effectively acts to screen the positive applied voltage. Therefore, the effects of the self-consistent field can essentially be modeled by a smaller applied bias.
The Poisson and the von Neumann equation form a system of coupled nonlinear differential equations which is usually solved by an iteration between Poisson's and von Neumann's equation.
The potential ![]() which enters the Schrödinger equation
(see Figure 7.1)
is
the sum of the solution
which enters the Schrödinger equation
(see Figure 7.1)
is
the sum of the solution ![]() of the Poisson equation
and an
of the Poisson equation
and an ![]() from the
materials' bandgap
from the
materials' bandgap
| (7.18) |
| (7.19) |
![\includegraphics[width=0.9\columnwidth
]{Figures/potential}](img587.png)
|
In order to solve the coupled system, we have used the Gummel method [Gum64], which takes into account the exponential dependence of the density on the potential. We follow the approach from [BAPGR02].
With this the step for updating the potential in the iteration is given by
![$\displaystyle \frac{d}{dx}[\epsilon(x)\frac{d}{dx} \phi_s^{\mathrm{new}}] = e\l...
...thrm{new}} - \phi_s^{\mathrm{old}}}{\phi_{\mathrm{ref}}}\right) - C\right) .$](img588.png) |
(7.20) |
Further details can be found in [BAPGR02], where this method, which is based on classical assumptions, was introduced.
![]()
![]()
![]()
![]() Previous: 7.2.2 Open System
Up: 7.2 The Open Von
Next: 7.2.4 A Brute Force
Previous: 7.2.2 Open System
Up: 7.2 The Open Von
Next: 7.2.4 A Brute Force