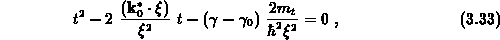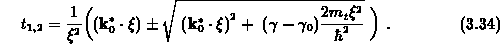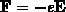Für die folgende Integration der Newtonschen Bewegungsgleichung 3.27 wird vorausgesetzt, daß der Ortsraum diskretisiert und daß das Kraftfeld innerhalb eines Diskretisierungsvolumens konstant ist. Diese Annahme ist konsistent mit der im Bauelementesimulator MINIMOS [46] verwendeten Diskretisierung der Poissongleichung [93], wo ebenfalls eine lineare Variation des elektrostatischen Potentials und damit ein konstantes elektrisches Feld zwischen zwei Gitterpunkten vorausgesetzt wird. Die folgende Integration gilt nur für Zeiten, in denen sich das Teilchen in einer bestimmten Gitterzelle aufhält. Soll die Berechnung über eine größere Zeit erfolgen, muß die Berechnung auch in der jeweiligen benachbarten Zelle mit dem entsprechenden Wert für das elektrische Feld ausgeführt werden und die Gesamttrajektorie aus den Teilstücken in den Zellen zusammengesetzt werden.
Im folgenden wird in die Newtonschen Bewegungsgleichung
3.27 für die Kraft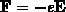 
gesetzt,
die Herring-Vogt-Transformation 3.12 angewendet und die
Abkürzung
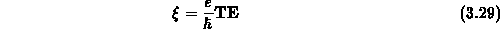
eingeführt. Dann lautet die Bewegungsgleichung i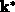m 
-Raum
und es kann die einfache Lösung
angegeben werden.
Die Änderung des transformierten Wellenvektors 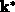ist also linear
in der Zeit. Die zeitliche
Entwicklung der Energie wird über Gleichung 3.17 durch die
Bandformfunktion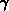 
bestimmt
Bei der Implementierung eines Monte-Carlo-Algorithmus stellt sich auch
die umgekehrte Frage, wann also eine bestimmte Energie und damit ein
bestimmtes 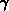erreicht wird. Dies erfordert die Lösung der
quadratischen Gleichung
