 ergibt sich, indem bei der Integration
der differentiellen Streurate (Gleichung 3.62) über alle
möglichen Endzustände
ergibt sich, indem bei der Integration
der differentiellen Streurate (Gleichung 3.62) über alle
möglichen Endzustände 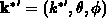 nur über die
Länge
nur über die
Länge 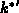 und den Azimutwinkel
und den Azimutwinkel 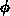 integriert wird, die
integriert wird, die
 Integration jedoch offen bleibt. Die Integration findet wieder im
transformierten
Integration jedoch offen bleibt. Die Integration findet wieder im
transformierten 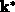 -Raum statt, wobei die z-Achse des
verwendeten Kugelkoordinatensystems mit dem Wellenvektor vor der Streuung
-Raum statt, wobei die z-Achse des
verwendeten Kugelkoordinatensystems mit dem Wellenvektor vor der Streuung
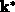 zusammenfällt,
zusammenfällt,




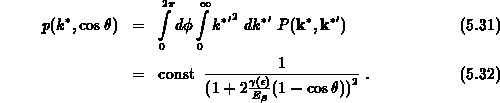
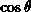 ergibt sich durch Integration der Dichte
ergibt sich durch Integration der Dichte
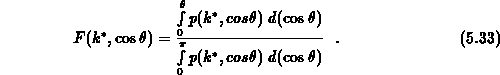
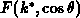 analytisch berechnet werden kann
und daß zusätzlich die Umkehrfunktion gebildet werden kann.
Unter diesen Voraussetzungen ist es möglich, wieder die direkte Methode
zur Erzeugung von Zufallszahlen anzuwenden.
Aus einer zwischen
analytisch berechnet werden kann
und daß zusätzlich die Umkehrfunktion gebildet werden kann.
Unter diesen Voraussetzungen ist es möglich, wieder die direkte Methode
zur Erzeugung von Zufallszahlen anzuwenden.
Aus einer zwischen
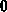 und
und 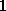 gleichverteilten Zufallszahl
gleichverteilten Zufallszahl  kann der
Streuwinkel direkt durch Lösen der Gleichung
kann der
Streuwinkel direkt durch Lösen der Gleichung
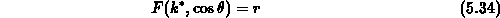
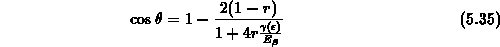
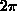 gleichverteilt.
gleichverteilt.