


Next: 6.3 Results and Discussion
Up: 6. Space Charge Limited
Previous: 6.1 Introduction
The SCLC problem in dielectrics can be described by the following equations [107]
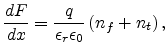 |
(6.1) |
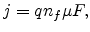 |
(6.2) |
where 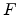 is the electric field intensity,
is the electric field intensity,
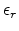 is the relative dielectric permittivity,
is the relative dielectric permittivity, 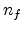 and
and 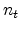 are the concentrations of the mobile and trapped
carriers, respectively,
are the concentrations of the mobile and trapped
carriers, respectively, 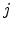 is the current density, and
is the current density, and 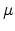 is the drift
mobility of carriers.
is the drift
mobility of carriers.
In this model, a Gaussian DOS function is assumed. Analysis of the optical adsorbtion
spectrum and mobility for PPV indicates that the DOS can be fitted well to a
Gaussian distribution with
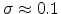 eV. In other disordered
molecular materials
eV. In other disordered
molecular materials 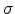 typically lies between
typically lies between 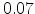 and
and 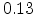 eV
[9].
eV
[9].
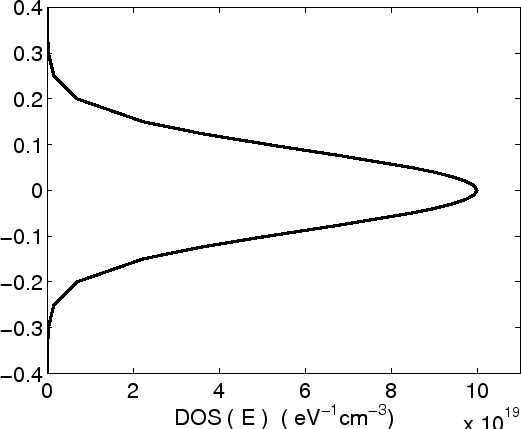
Figure 6.1:
Gaussian density of states with zero mean energy. The vertical axis corresponds to energy,
the horizontal axis reflects the site density. The center of the Gaussian DOS is
at zero energy.
|
|
A schematic representation of the Gaussian DOS is shown in Fig 6.1. In the
tail of the distribution few sites are available for hopping and their nearest
neighbors are many 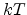 away in energy, so that they serve as trap
centers. Site-selective fluorescence of PPV has also shown that the sites in
the tail of the distribution act as traps [125]. While the sites
towards the center of DOS more neighbors are accessible and the energy
between them is very close. So they provide the mobile carriers. Here we define
a conduction edge [126] at about
away in energy, so that they serve as trap
centers. Site-selective fluorescence of PPV has also shown that the sites in
the tail of the distribution act as traps [125]. While the sites
towards the center of DOS more neighbors are accessible and the energy
between them is very close. So they provide the mobile carriers. Here we define
a conduction edge [126] at about 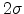 below the Gaussian center. We do not
rigorously justify such edge position and it is done only for illustration
purpose, though it is similar to the method applied to absorption spectrum or
STM measurements [127]. So the concentrations of mobile and
trapped carriers can be calculated as
below the Gaussian center. We do not
rigorously justify such edge position and it is done only for illustration
purpose, though it is similar to the method applied to absorption spectrum or
STM measurements [127]. So the concentrations of mobile and
trapped carriers can be calculated as
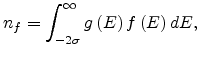 |
(6.3) |
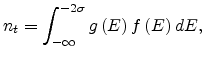 |
(6.4) |
with
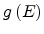 being the DOS function and
being the DOS function and
![$ f\left(E\right)=\left(1+\exp\left[E-E_F\right]\right)^{-1}$](img527.png) the Fremi-Dirac
distribution. Substituting (6.3) and
(6.4) into (6.1)
and (6.2), we obtain
the Fremi-Dirac
distribution. Substituting (6.3) and
(6.4) into (6.1)
and (6.2), we obtain
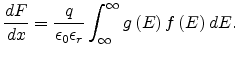 |
(6.5) |
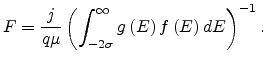 |
(6.6) |
Then differentiate (6.6) with respect to 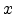 to obtain the equation
to obtain the equation
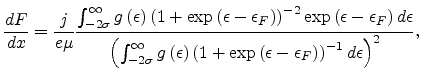 |
(6.7) |
where
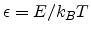 and
and
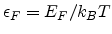 . Substituting (6.7) into (6.5), we obtain the
differential equation for quasi Fermi-energy as
. Substituting (6.7) into (6.5), we obtain the
differential equation for quasi Fermi-energy as
where
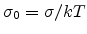 . Combing (6.6) and (6.8), we obtain the
position-dependent
electric field. the
. Combing (6.6) and (6.8), we obtain the
position-dependent
electric field. the 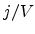 characteristics can be
calculated by integrating the field over the coordinate.
characteristics can be
calculated by integrating the field over the coordinate.



Next: 6.3 Results and Discussion
Up: 6. Space Charge Limited
Previous: 6.1 Introduction
Ling Li: Charge Transport in Organic Semiconductor Materials and Devices
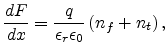
![]() eV. In other disordered
molecular materials
eV. In other disordered
molecular materials ![]() typically lies between
typically lies between ![]() and
and ![]() eV
[9].
eV
[9].
![]() away in energy, so that they serve as trap
centers. Site-selective fluorescence of PPV has also shown that the sites in
the tail of the distribution act as traps [125]. While the sites
towards the center of DOS more neighbors are accessible and the energy
between them is very close. So they provide the mobile carriers. Here we define
a conduction edge [126] at about
away in energy, so that they serve as trap
centers. Site-selective fluorescence of PPV has also shown that the sites in
the tail of the distribution act as traps [125]. While the sites
towards the center of DOS more neighbors are accessible and the energy
between them is very close. So they provide the mobile carriers. Here we define
a conduction edge [126] at about ![]() below the Gaussian center. We do not
rigorously justify such edge position and it is done only for illustration
purpose, though it is similar to the method applied to absorption spectrum or
STM measurements [127]. So the concentrations of mobile and
trapped carriers can be calculated as
below the Gaussian center. We do not
rigorously justify such edge position and it is done only for illustration
purpose, though it is similar to the method applied to absorption spectrum or
STM measurements [127]. So the concentrations of mobile and
trapped carriers can be calculated as