


Next: 3.1 Boundary-Value Problems
Up: Dissertation Alexandre Nentchev
Previous: 2.7 Institute for Microelectronics
Contents
3. Introduction to the Finite Element Method
Normally the problems arising from mathematical physics
are described by partial differential equation
systems [13,14,15,16]
defined
in a given domain of interest. These boundary value problems
represent the models of specific problems for further
simulation and analysis [17] and
are usually approximately solved by numerical procedures.
One of these procedures is the finite element method. Originally this
method has been successfully applied to mechanical
problems [18,19]. Today, the finite
element method is the general technique widely used for
mathematical and engineering numeric analysis.
A lot of books and scripts have been
issued to help understanding and applying this interesting and useful
topic [20,21,22,23,24,25,26,27,28]. The method is also
well suited for object-oriented treatment [29],
which is essential for software implementation. Further enhancement
of the finite element method can be achieved by formulating self-adapting
procedures and techniques to solve open region
problems [30] and by the analysis of the error
in the computed finite element solution [31,32].
There are two most widely used classical methods for approximation of
boundary-value problems. One is the Ritz Method and the other is Galerkin's
method [33,34].
The Ritz method3.1 is a variational method. It formulates
the boundary value problem in terms of a variational expression,
called functional. Galerkin's method belongs to the family
of weighted residual methods. These two methods build the foundation
of modern finite element analysis. In this work Galerkin's
approach is preferred for the introduction of the finite element method.
In general an area
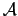 is enclosed in its boundary
is enclosed in its boundary
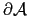 which usually consists of several closed curves.
Closed surfaces have no boundary (
which usually consists of several closed curves.
Closed surfaces have no boundary (
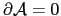 ). Analogously
the boundary
). Analogously
the boundary
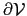 of a three-dimensional domain
of a three-dimensional domain
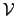 can be represented by one or more closed surfaces.
The unit normal vector to the boundary curve
can be represented by one or more closed surfaces.
The unit normal vector to the boundary curve
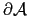 for the
two-dimensional case or to the boundary surface
for the
two-dimensional case or to the boundary surface
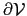 for
the three-dimensional case, respectively, is denoted as
for
the three-dimensional case, respectively, is denoted as 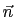 . It has
the characteristic length one and points outward.
. It has
the characteristic length one and points outward.
Subsections



Next: 3.1 Boundary-Value Problems
Up: Dissertation Alexandre Nentchev
Previous: 2.7 Institute for Microelectronics
Contents
A. Nentchev: Numerical Analysis and Simulation in Microelectronics by Vector Finite Elements
![]() is enclosed in its boundary
is enclosed in its boundary
![]() which usually consists of several closed curves.
Closed surfaces have no boundary (
which usually consists of several closed curves.
Closed surfaces have no boundary (
![]() ). Analogously
the boundary
). Analogously
the boundary
![]() of a three-dimensional domain
of a three-dimensional domain
![]() can be represented by one or more closed surfaces.
The unit normal vector to the boundary curve
can be represented by one or more closed surfaces.
The unit normal vector to the boundary curve
![]() for the
two-dimensional case or to the boundary surface
for the
two-dimensional case or to the boundary surface
![]() for
the three-dimensional case, respectively, is denoted as
for
the three-dimensional case, respectively, is denoted as ![]() . It has
the characteristic length one and points outward.
. It has
the characteristic length one and points outward.