next up previous contents
Next: 4.2 Three-Dimensional Scalar Finite Up: 4.1 Two-Dimensional Scalar Finite Previous: 4.1.4 Assembling   Contents


4.1.5 Neumann Boundary Condition

For the previous examination the Neumann boundary condition (4.17) on $ \mathcal{C}_N$ is assumed to be zero (homogeneous Neumann boundary condition). This subsection discusses which consequences are drown from this assumption. Furthermore, it presents specific models which require inhomogeneous (or non-zero) Neumann boundary conditions to be assigned to define the field quantities or even to preserve the physical consistence.

For the electrostatic case using (4.5), (4.8), and (4.10) it is written

$\displaystyle \vec{\nabla}\cdot\left(\utilde{\gamma}\cdot\vec{\nabla}\varphi\right) = 0.$ (4.50)

Considering (3.18) the Neumann boundary condition is given by the conormal derivative of the electrostatic potential $ \varphi$ or by the normal component of the current density, respectively

$\displaystyle J_n = \vec{n}\cdot\vec{J} = -\vec{n}\cdot\left(\utilde{\gamma}\cdot\vec{\nabla}\varphi\right) \mathrm{on} \mathcal{C}_N.$ (4.51)

Thus, for a boundary value problems like (4.50) the normal current density or the corresponding total current forced in the simulation domain can be given by applying inhomogeneous Neumann boundary condition on $ \mathcal{C}_N$  [50]. The same holds true for thermic problems. External sources impressing a normal heat flux density on an outer boundary part represent inhomogeneous Neumann boundary conditions [10].

However, the Neumann boundary condition cannot be arbitrarily chosen. For example, in the electrostatic case given by (4.11), Gauß's law (4.4) requires that the total electric flow through the boundaries must be equal to the electric charge inside the domain. For the two-dimensional case this is given by the expression

$\displaystyle \int_{\mathcal{A}}\vec{\nabla}\cdot\vec{D} \mathrm{d}A = \int_{\... ...t\vec{\nabla}\varphi\right) \mathrm{d}s = \int_{\mathcal{A}}\rho \mathrm{d}A.$ (4.52)

According to (3.18) the Neumann boundary condition of (4.11) is (4.52). In this case, if the surface electric charge in the entire domain $ \mathcal{A}$ does not vanish, physically it doesn't make sense to apply homogeneous Neumann boundary conditions allover the entire boundary $ \partial\mathcal{A}$ .

In this work for the approximation of the inhomogeneous Neumann boundary condition an extension of the sum (4.13) with (4.22) from Section 4.1 is used

$\displaystyle \tilde{\varphi}(\vec{r}) = \sum_{j=m+1}^lc_j\lambda_j.$ (4.53)

The coefficients are indexed in the following way: The entire discretized domain contains $ m$ nodes. The unknown coefficients numbered from $ 1$ to $ n$ correspond to the nodes which do not lie on the Dirichlet boundary (the non-Dirichlet nodes). The known coefficients numbered from $ n{+}1$ to $ m$ ($ n < m$ ) correspond to the nodes on the Dirichlet boundary (the Dirichlet nodes). The coefficients $ c_j$ from (4.53) ($ m < l$ ) must be obtained from the Neumann boundary condition (4.17) on the Neumann boundary $ \mathcal{C}_N$ . Thus, if $ \vec{E}$ on the Neumann boundary is given

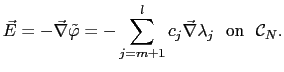$\displaystyle \vec{E} = -\vec{\nabla}\tilde{\varphi} = -\sum_{j=m+1}^lc_j\vec{\nabla}\lambda_j \mathrm{on} \mathcal{C}_N.$ (4.54)

In an element (Fig. <4.1>), from which one or more edges are part of the Neumann boundary $ \mathcal{C}_N$ $ \vec{E}$ is given by

\begin{displaymath}\begin{split}\vec{E}^e = -\vec{\nabla}\varphi^e = -\sum_{j=1}... ..._{31} \vec{n}_2 + c_3^e l_{12} \vec{n}_3\right). \end{split}\end{displaymath} (4.55)

To express a given $ \vec{E}$ on $ \mathcal{C}_N$ some of the coefficients $ c_1^e$ , $ c_2^e$ and $ c_3^e$ can be set to zero. Let the Edge $ 23$ in the element from Fig. <4.1> be part of the Neumann boundary. If $ \vec{E}$ is normal to the Edge $ 23$ , then $ c_2^e$ and $ c_3^e$ can be set to zero. Otherwise $ c_1^e$ can be set to zero and $ c_2^e$ and $ c_3^e$ are calculated from $ \vec{E}$ on $ \mathcal{C}_N$ .

Now the Neumann boundary integral from (4.21) is given by

$\displaystyle \int_{\mathcal{C}_N}\lambda_iD_n \mathrm{d}s = \sum_{j=m+1}^lc_j... ...vec{\nabla}\lambda_j\right) \mathrm{d}s = \sum_{j=m+1}^lc_jM_{ij}, i\in[1;n].$ (4.56)

The corresponding element matrix $ [M]^e$ for $ \epsilon$ assumed as a constant scalar in each element, is given in the appendix in Subsection B.2.1, which also refers to the magnetic scalar potential and instead of $ \epsilon$ and $ \varphi$ the tokens $ \mu$ and $ \psi$ are used.

Figure 4.5: Homogeneous Neumann boundary conditions on the outer boundary $ \mathcal{C}_N$ .
\includegraphics[width=14cm,height=9.6cm]{figures/scalarfem2d/dissneumann.eps}



Figure 4.6: The outer region is cut off at $ \mathcal{C}_N$ .
\includegraphics[width=14cm,height=9.6cm]{figures/scalarfem2d/bigdissneumann.eps}

The acceptance of homogeneous Neumann boundary conditions is only an approximation, which is not generally valid. This will be demonstrated by an example. Let us consider the field generated by two electrodes with different electrostatic potential applied. Let there be no other potential or charge density distributions close to these electrodes to disturb this field. On the first electrode 0 V and on the second one $ 1$ V is impressed as shown in Fig. <4.5>, which is given by Dirichlet boundary conditions for the boundaries $ \mathcal{C}_{D1}$ and $ \mathcal{C}_{D2}$ between the simulation domain $ \mathcal{A}$ and the electrodes. The Laplace equation (4.12) for the electric potential is solved in $ \mathcal{A}$ . As usual, homogeneous Neumann boundary conditions are set to the outer boundary $ \mathcal{C}_N$ . This will not influence the result, if the Neumann boundary is infinitely far away from the electrodes and the corresponding Neumann boundary conditions can be neglected. In practice it is simulated with finite lengths which normally results in simulation error. To demonstrate this behavior the same electrode configuration is analyzed in a domain nine times larger than the domain in Fig. <4.5>. Then the domain is cut off to the same region size as in Fig. <4.5>. The corresponding electrostatic potential distribution is shown by equipotential lines in Fig. <4.6>. This is compared to the field in Fig. <4.5>. In contrast to Fig. <4.5> the field on Fig. <4.6> corresponds to the expected one for the given configuration. The homogeneous Neumann boundaries have distorted the simulation result in the small area on Fig. <4.5>. Of coarse this is a systematic error, it gets smaller with growing simulation domains. For simulation of open regions the finite element method can be combined with the boundary element method [51,52,53]. This can also be performed with the so called edge elements [54] introduced in Chapter 5.

next up previous contents
Next: 4.2 Three-Dimensional Scalar Finite Up: 4.1 Two-Dimensional Scalar Finite Previous: 4.1.4 Assembling   Contents
A. Nentchev: Numerical Analysis and Simulation in Microelectronics by Vector Finite Elements