2.6.1 Electron-Phonon Matrix Elements
An important case is the intra-subband scattering of electrons, 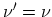 ,
therefore,
,
therefore,  (Fig. 2.11-b) and
(Fig. 2.11-b) and 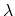 can be any of six different
phonon polarizations. One can omit the index
can be any of six different
phonon polarizations. One can omit the index  and write the phonon
frequency as
and write the phonon
frequency as
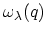 and the reduced electron-phonon matrix
element for a given band as
and the reduced electron-phonon matrix
element for a given band as
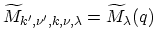 , where the
weak dependence on
, where the
weak dependence on 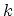 is neglected.
is neglected.
For intra-valley processes, most of the phonons have
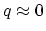 and are
referred to as
and are
referred to as 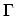 -point phonons. Near the
-point phonons. Near the 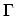 point a linear
dispersion relation for acoustic phonons is assumed,
point a linear
dispersion relation for acoustic phonons is assumed,
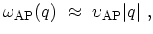 |
(2.16) |
where
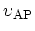 is the acoustic phonon velocity. For
optical phonons the energy is assumed to be independent of the phonon
wave-vector
is the acoustic phonon velocity. For
optical phonons the energy is assumed to be independent of the phonon
wave-vector
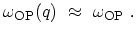 |
(2.17) |
Near the
 -point the reduced electron-phonon matrix elements can be approximated by
-point the reduced electron-phonon matrix elements can be approximated by
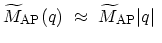 |
(2.18) |
for acoustic phonons and by
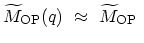 |
(2.19) |
for optical phonons [56].
Phonons inducing inter-valley processes have a wave-vector of
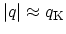 , where
, where
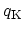 is a wave-number corresponding to the
is a wave-number corresponding to the
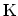 -point of the Brillouin
zone of graphite. For such phonons one can neglect the q-dependence,
-point of the Brillouin
zone of graphite. For such phonons one can neglect the q-dependence,
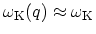 and
and
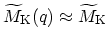 [56].
[56].
To calculate the electron-phonon matrix elements one can employ the orthogonal
tight-binding [57], the non-orthogonal tight-binding [56], and
density functional theory [58] for the band-structure and a
force constant model for the lattice dynamics [59,12].
Electron-phonon matrix elements depend on the chirality and the diameter of the
CNT [57,56,58]. Figure 2.12 shows the
reduced matrix elements for intra-subband intra-valley transitions in
semiconducting zigzag and chiral CNTs as a function of the CNT
radius [56].
Figure 2.12:
The calculated intra-valley intra-subband
reduced electron-phonon matrix elements of acoustic (in eV) and
optical phonons (in eV/Å) for zigzag (open circles) and chiral
(closed) CNTs with the radius range from 3.5 Å to 12 Å. The results for
CNTs with residuals 1 and 2 of the division  by 3 are shown in the left
and right figures, respectively. Open and closed circles denote the
results for zigzag (Z) and chiral (C) CNTs, respectively. All
results are for the lowest conduction band [56].
by 3 are shown in the left
and right figures, respectively. Open and closed circles denote the
results for zigzag (Z) and chiral (C) CNTs, respectively. All
results are for the lowest conduction band [56].
|
|
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors
![]() and are
referred to as
and are
referred to as ![]() -point phonons. Near the
-point phonons. Near the ![]() point a linear
dispersion relation for acoustic phonons is assumed,
point a linear
dispersion relation for acoustic phonons is assumed,
![\includegraphics[width=0.97\textwidth]{figures/CZ1-CZ2.eps}](img345.png)