3.10.3 The WIGNER Distribution Function

Another approach capable of handling both quantum coherent propagation and dissipative scattering effects is based on the WIGNER distribution function. The Wigner quasi-probability distribution was introduced by WIGNER in 1932 [218] to study quantum corrections to classical statistical mechanics. The goal was to replace the wave-function that appears in the SCHRÖDINGER equation with a probability distribution in phase space. A classical particle has a definite position and momentum and hence, is represented by a point in phase space. For a collection (ensemble) of particles, the probability of finding a particle at a certain position in phase space is given by a probability distribution. This does not hold in quantum mechanics due to the uncertainty principle. Instead, the WIGNER quasi-probability distribution plays an analogous role, it is defined as the density matrix in a mixed coordinate/momentum representation [218,219]. But the WIGNER quasi-probability distribution does not satisfy all the properties of a probability distribution. On the other hand it satisfies boundedness properties unavailable to the classical distributions. For instance, the WIGNER distribution can and normally does go negative for states which have no classical model and a convenient indicator of quantum-mechanical interference.

Applying the WIGNER-WEYL transformation to the LIOUVILLE equation gives the kinetic equation for the WIGNER function

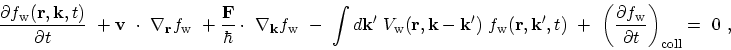$$\begin{array}{l}\displaystyle \frac{\partial f_\mathrm{w}({\... ...rm{w}}{\partial t}\right)}_\mathrm{coll} = \ 0 \ , \end{array}$$ (3.94)

where the kernel of the potential operator is given by

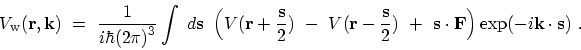$$\begin{array}{l}\displaystyle V_\mathrm{w}({\bf r},{\bf k}) ... ...f F}\right)\mathrm{exp}(-i{\bf k}\cdot{\bf s}) \ . \end{array}$$ (3.95)

A practically used approximation to incorporate realistic scattering processes into the WIGNER equation is to utilize the BOLTZMANN scattering operator [220,219], or by an even simpler scheme such as the relaxation time approximation[221]. The inclusion of dissipation through the BOLTZMANN scattering operator, although intuitively appealing, raises some concerns about the validity of such procedure. The BOLTZMANN scattering operator is semi-classical by its nature, and represents a good approximation for sufficiently smooth device potentials. To account for scattering more rigorously, spectral information has to be included into the WIGNER function, resulting in an energy-dependence in addition to the momentum dependence [190].

The kinetic equation for the WIGNER function is similar to the semi-classical BOLTZMANN equation, except for a non-local potential term. In the case of a slowly varying potential this non-local term reduces to the local classical force term, and the semi-classical description given by the BOLTZMANN equation is obtained from the WIGNER equation. The BOLTZMANN equation is the basis for the standard models of electron transport in semiconductors in a semi-classical approximation. By far the most widely used technique for solving the BOLTZMANN equation has been the Monte Carlo method [222]. Transport models based on the BOLTZMANN transport equation can be derived using the method of moments [223,224,225] which yields the drift-diffusion model [226], the energy-transport and hydrodynamic models [227], or higher-order transport models [228]. Furthermore, an approximate solution can be obtained by expressing the distribution function as a series expansion which leads to the spherical harmonics approach [229,230].

M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors