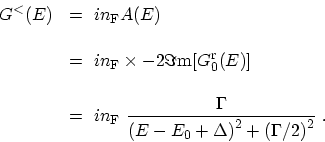The non-interacting GREEN's functions for electrons are given
by (D.6). For a bound state with the
well-defined energy 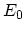 the GREEN's function is given by
the GREEN's function is given by
![$ G^\mathrm{r}_0(E)={[E-E_0+i\eta]}^{-1}$](img881.png) , where
, where 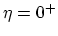 is a small positive
number. The renormalized retarded GREEN's function in the presence of
interaction is given by the DYSON equation
is a small positive
number. The renormalized retarded GREEN's function in the presence of
interaction is given by the DYSON equation
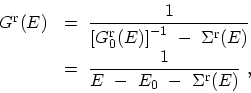 |
(4.57) |
The self-energy has imaginary and real parts
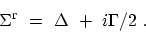 |
(4.58) |
The imaginary part is interpreted as
damping of the particle motion. It is related to the finite life-time of
the state. The real part causes an energy shift,
which may also change the effective mass or group velocity.
Under equilibrium condition the lesser GREEN's function is given by
(see (D.10))
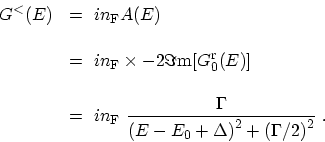 |
(4.59) |
The lesser GREEN's function is of LORENTZian shape [60].
The peak of the resonance is shifted by 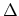 and is broadened by
and is broadened by 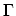 ,
as shown in the inset of Fig. 4.10. In open systems, localized states broaden due
to the coupling to contacts (
,
as shown in the inset of Fig. 4.10. In open systems, localized states broaden due
to the coupling to contacts ( ), even in the absence of scattering
processes.
), even in the absence of scattering
processes.
The electron concentration for each of the confined states can be calculated as
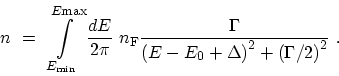 |
(4.60) |
We assume that the FERMI level is far above the resonance,
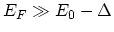 , so that the FERMI factor can be replaced by
1. Equation (4.60) is used as a reference function for comparing
the results of different numerical integration methods.
, so that the FERMI factor can be replaced by
1. Equation (4.60) is used as a reference function for comparing
the results of different numerical integration methods.
M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors