3.2.3 Mixed Operations
There are operations which can neither be classified as purely topological or purely geometrical.
The most popular operations, being mesh refinement algorithms, are presented in this section.
Mesh refinement algorithms are similar to flips, where a number of cells is replaced by another configuration of cells.
In contrast to flips, mesh refinement algorithms also require that every cell of the input mesh is a union of cells of the refined mesh. In other words, the refined mesh has to respect the original mesh.
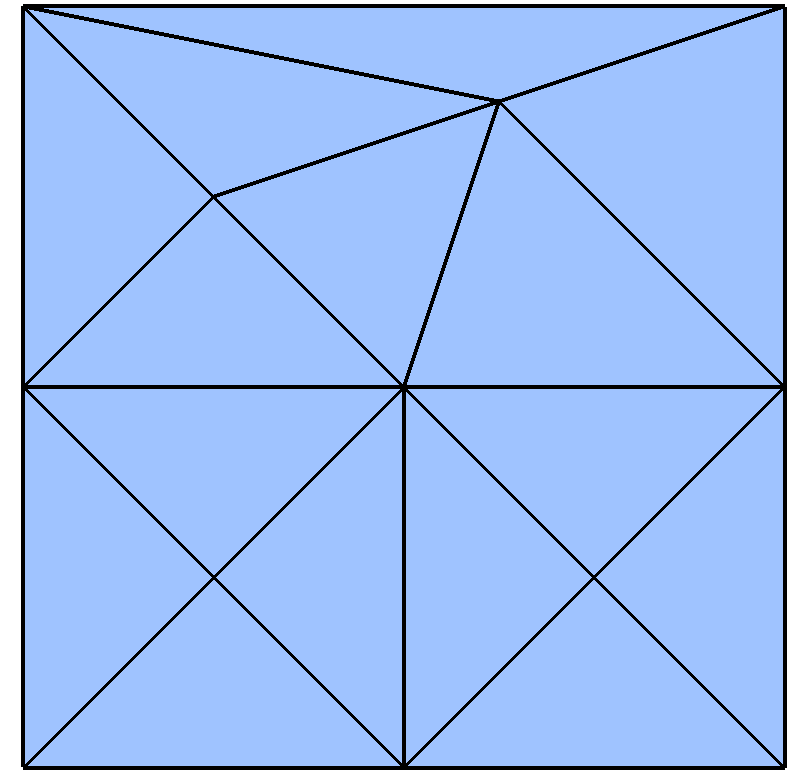
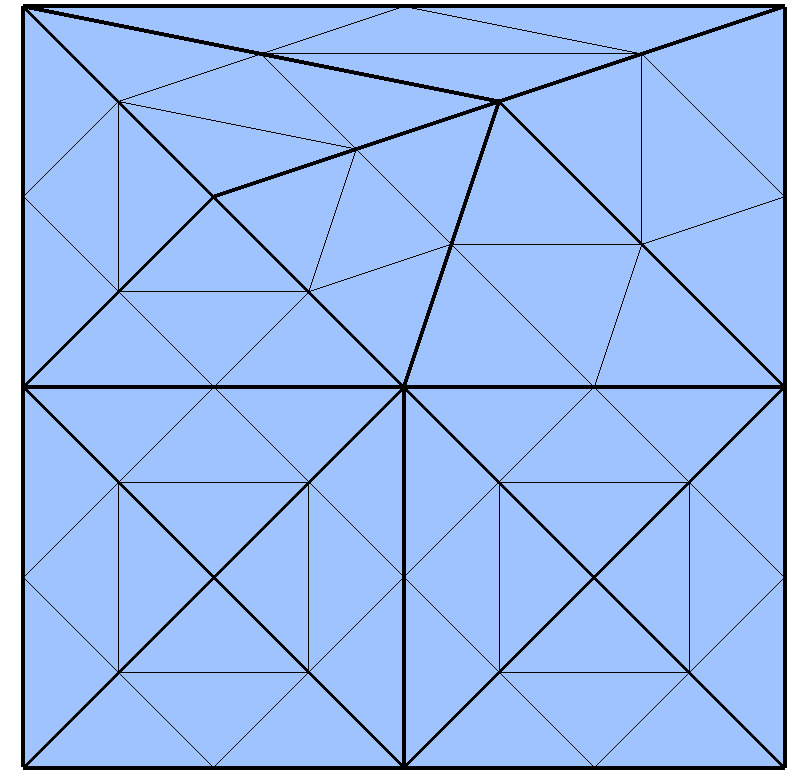
Figure 3.6:
2D simplex refinement
|
Every triangle of the initial mesh is refined into four new triangles. |
The main advantage of a refined mesh is that for every refined cell there is exactly one parent cell in the original mesh. This is particularly useful when transferring additional meta information stored on elements from the original mesh to the refined mesh or vice versa.
Figure 3.6 shows an example of a mesh refinement.
A popular type of refinement uses edge bi- or trisection operations, where an edge is marked for refinement and split into two or three new edges.
For each element type there are rules on how to replace a cell with a specific configuration of marked edges by refined cells.
To ensure element quality, additional edges can be marked for refinement.
For example, a popular refinement strategy using this approach is red-green-blue refinement [34].
Such types of refinement algorithms have lower bounds for some element qualities, like the smallest angle [55].
Trisection of quadrilaterals and hexahedrons is frequently used in favor of bisection [114].
Mesh refinement is often utilized in adaptive processes for boundary value problems, where error estimators are used to locally increase the accuracy of the solution.
Error estimators detect mesh elements, where the difference of the numerical solution and the real solution is high, and mark those for refinement.
A related algorithm is Delaunay mesh refinement of simplex meshes [21]. Delaunay mesh refinement cannot be considered a classical refinement algorithm, because in general there are cells in the refined mesh which do not respect the original mesh.
Delaunay mesh refinement incrementally inserts vertices in a mesh, which already is Delaunay.
A popular Delaunay mesh refinement algorithm is the Bowyer-Watson algorithm [42].
Given a specific point
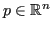 , all cells
, all cells  of a mesh are removed where
of a mesh are removed where
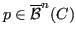 .
Every facet of these cells, which is also in the boundary of the union of these cells, is then connected to the point
.
Every facet of these cells, which is also in the boundary of the union of these cells, is then connected to the point  to form a new simplex cell.
It has been shown, that the new mesh is also Delaunay, if the original mesh is Delaunay. This statement also holds for constrained Delaunay with the modification that only cells which are visible to the newly inserted point are deleted.
Optimal locations for Delaunay mesh refinement can be determined by using a conflict graph [73].
to form a new simplex cell.
It has been shown, that the new mesh is also Delaunay, if the original mesh is Delaunay. This statement also holds for constrained Delaunay with the modification that only cells which are visible to the newly inserted point are deleted.
Optimal locations for Delaunay mesh refinement can be determined by using a conflict graph [73].
florian
2016-11-21
![\begin{defn}[Refined mesh]
Let ${({\mathcal{M}}, {\xi})}$\ and ${({\mathcal{R}},...
...s, C_k$\ of ${({\mathcal{M}}, {\xi})}$: $C = \bigcup_{i=1}^{k}{C_i}$.
\end{defn}](img536.gif)