2.1 Geometries
A simulation domain has to be specified by a geometry. To support discretization-based simulation methods, like the FEM, this geometry is required to have a Lipschitz 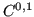 boundary [59].
In this work the geometry space
boundary [59].
In this work the geometry space
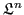 (cf. Definition A.25) is used to represent geometries.
(cf. Definition A.25) is used to represent geometries.
A geometry is not required to be connected. However, there always is a finite partition of a geometry, which consists of connected sets.
This is required for guaranteeing meshes with a finite number of mesh elements.
A geometry
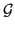 is called
is called 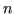 -dimensional, if
-dimensional, if
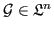 and if
and if
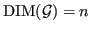 . If
. If
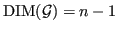 ,
,
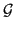 is called an
is called an 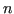 -dimensional hull geometry.
-dimensional hull geometry.
Figure 2.1:
Multi-region geometry
|
The wooden shaft (visualized in red) and steel head (visualized in lined blue) are separate regions. |
It is beneficial to partition the simulation domain for many simulation scenarios.
For example, different parts of a domain to be simulated are made of different materials.
It is of advantage to reflect these parts, called regions, in the geometry as well.
An example for a multi-region geometry is given in Figure 2.1, where the two materials of a hammer are represented by separate regions.
A simple approach for representing multi-region geometries is to add an additional region function
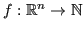 , which maps a point of the geometry to its region. However, if a geometry has more than two regions, this approach might lead to regions which are not closed.
Therefore, a multi-region geometry is defined using a function
, which maps a point of the geometry to its region. However, if a geometry has more than two regions, this approach might lead to regions which are not closed.
Therefore, a multi-region geometry is defined using a function
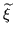 , which maps a point to the set of regions in which the point is located.
For example, for all points of the interior of a region, the function
, which maps a point to the set of regions in which the point is located.
For example, for all points of the interior of a region, the function
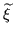 maps to just one region and for points, where multiple regions touch, it maps to all regions.
maps to just one region and for points, where multiple regions touch, it maps to all regions.
The interface of geometry regions is also equal to all points which are in all regions.
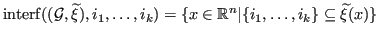 |
(2.1) |
Every multi-region geometry with
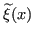 being a constant function can be identified with a geometry and vice versa.
being a constant function can be identified with a geometry and vice versa.
To enable computational use of geometries, a representation is needed.
There are three popular types of geometry representation:
- Implicit representation
- Boundary representation
- Constructive solid geometries (CSG)
Geometries of simulation domains in CAE are usually created using computer-aided design (CAD) tools and represented with boundary representation or constructive solid geometries. Data formats, like STEP [87] or IGES [46], are typically used to interface CAD applications with mesh generation software.
Subsections
florian
2016-11-21
![\begin{subfigure}[b]{0.9\textwidth}
\centering
\includegraphics[width=0.5\textwidth]{figures/hammer}
\end{subfigure}](img148.gif)