


 |  |  |
While the machines constructed to perform computational tasks undoubtedly are capable of addressing mathematical problems, it requires special adaptations in order to carry mathematical procedures from the purely theoretical settings to the machine world. The declarative parts of mathematical formalisms pose a problem for the implementation of algorithms. This is true even for very simple mathematical statements such as

The limited nature of the computing world also becomes apparent, when comparing the limited numerical data types available to the machine, which may require special attention from the programmer, to the plethora of sets a mathematician has at his command.
A very simple example concerns integers which are commonly denoted as 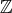 in mathematics. While
programming languages offer a data type of exactly the same name, it falls far short from the
mathematical entity, with which it shares its name. The most apparent fact is that the data
type encompasses only a finite amount of distinct elements, which directly corresponds to
the amount of memory it requires, while
in mathematics. While
programming languages offer a data type of exactly the same name, it falls far short from the
mathematical entity, with which it shares its name. The most apparent fact is that the data
type encompasses only a finite amount of distinct elements, which directly corresponds to
the amount of memory it requires, while 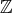 is infinite and has no resource consumption
associated with it. Furthermore, while both cases are groups, the topology of integer data types
resembles
is infinite and has no resource consumption
associated with it. Furthermore, while both cases are groups, the topology of integer data types
resembles 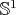 , as shown in the left part of Figure 3.5 where the minimum and maximum
values are next to each other and wrap around, which substantially deviates from the
, as shown in the left part of Figure 3.5 where the minimum and maximum
values are next to each other and wrap around, which substantially deviates from the 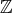 topology.
topology.
In the case of floating point data types, such as defined by IEEE 754 [30], which are used to emulate the
mathematical concepts of the rational numbers 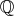 and the real numbers
and the real numbers 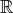 , are at best capable of
exactly representing a subset of
, are at best capable of
exactly representing a subset of 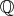 , but fail to capture irrational numbers at all. While the topology of
this data type is linear for the numbers it represents, there is also an isolated element
, but fail to capture irrational numbers at all. While the topology of
this data type is linear for the numbers it represents, there is also an isolated element 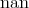 , as is
depicted in the right half of Figure 3.5. Furthermore, while being a super set of the integer data type, it
fails to be a group.
, as is
depicted in the right half of Figure 3.5. Furthermore, while being a super set of the integer data type, it
fails to be a group.
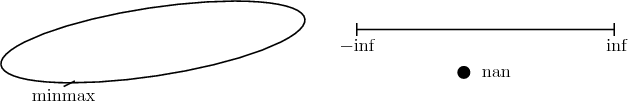
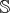 type topology. The data type on
the right even includes an isolated point (nan).
type topology. The data type on
the right even includes an isolated point (nan). While being far from comprehensive, the given examples should indicate that care has to be taken, when considering implementing algorithms on a digital computer. An awareness of a machine’s limitations, which may vary considerably due to architecture and platform, is essential for realizing reliable scientific computing applications.
 |  |  |