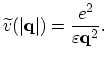B. Random Phase Approximation and Plasmons

Random phase approximation (RPA) is obtained by summing all chain Feynman diagrams. The sequence of chain diagrams can be summed by writing an integral equation which iterates the addition of a single link. The single link is shown in Fig. B.1.

Figure B.1: Feynman diagram for a single link.

The corresponding response function for a non-interacting system is thus given as [84]:

$$D_{0}(\vec{q},\omega)=2\sum_{v}\int\frac{d^{3}k}{(2\pi)^{2}} \big... ...k}))}{\omega+\epsilon_{v}(\vec{k})-\epsilon_{v}(\vec{k}+\vec{q})-i\eta}\biggr],$$ (B.1)

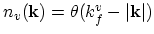where $n_{v}(\vec{k})=\theta(k^{v}_{f}-\vert\vec{k}\vert)$. For small 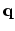$\vec{q}$ one obtains from (B.1):

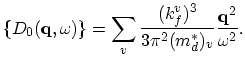$$\{D_{0}(\vec{q},\omega)\}=\sum_{v}\frac{(k_{f}^{v})^{3}}{3\pi^{2}(m^{*}_{d})_{v}}\frac{\vec{q}^{2}}{\omega^{2}}.$$ (B.2)

Summation over all direct RPA chain diagrams gives for the particle-hole Green's function:

$$G^{RPA}(\vec{k}_{1}+\vec{q},\vec{k}_{1}\vert\vec{k}_{2}+\vec{q},\... ...c{q},\omega)} {1-\widetilde{v}(\vert\vec{q}\vert)D_{0}(\vec{q},\omega)}\biggr],$$ (B.3)

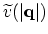where $\widetilde{v}(\vert\vec{q}\vert)$ is the direct matrix element which only depends on the momentum transfer $\vert\vec{q}\vert$.

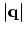Since the poles of the Green's function give the excited states of the system, in RPA the excited states occur at 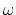$\omega$ such that:

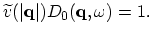$$\widetilde{v}(\vert\vec{q}\vert)D_{0}(\vec{q},\omega)=1.$$ (B.4)

In the case of electron gas for the Coulomb potential the direct matrix element becomes:

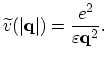$$\widetilde{v}(\vert\vec{q}\vert)=\frac{e^{2}}{\varepsilon \vec{q}^{2}}.$$ (B.5)

This equation together with (B.2) gives the expression for the plasmon frequency (2.133).

S. Smirnov: