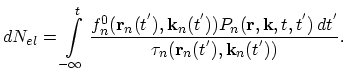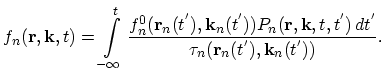To understand the structure of a non-equilibrium state and the difference from an equilibrium state it is useful to consider the relaxation time
approximation before the general theory. The relaxation time
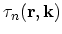 is introduced in a way that the
collision probability during the time interval
is introduced in a way that the
collision probability during the time interval  for an electron in band
for an electron in band 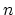 at phase space point
at phase space point
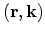 is equal to
is equal to
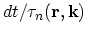 . In the relaxation time approximation it is inferred that some time after scattering has occurred the electron distribution
does not depend on the non-equilibrium distribution just before the scattering. Additionally, if electrons have the equilibrium distribution with local
temperature
. In the relaxation time approximation it is inferred that some time after scattering has occurred the electron distribution
does not depend on the non-equilibrium distribution just before the scattering. Additionally, if electrons have the equilibrium distribution with local
temperature
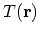 :
:
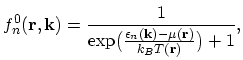 |
(2.37) |
the collisions do not affect the form of the distribution function. Therefore this approximation surmises that the information about the non-equilibrium
state is completely lost due to the scattering processes2.10 and that the thermodynamic equilibrium corresponding to a local temperature is maintained through the scattering. This totally
specifies the distribution function of those electrons, which have been scattered near point 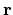 between
between 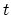 and
and 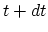 . This distribution function
is denoted as
. This distribution function
is denoted as
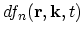 . It cannot depend on the non-equilibrium distribution function
. It cannot depend on the non-equilibrium distribution function
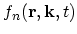 . Thus
. Thus
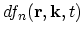 can be found assuming an arbitrary form of
can be found assuming an arbitrary form of
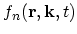 . This can be done for example using expression
(2.37) for the local equilibrium taking into account the fact that the collisions do not change its form. During a time interval
. This can be done for example using expression
(2.37) for the local equilibrium taking into account the fact that the collisions do not change its form. During a time interval 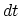 an
electron fraction
an
electron fraction
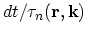 in band
in band 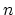 with quasi-momentum
with quasi-momentum
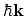 and coordinate
and coordinate 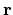 are scattered, changing their
band
number and quasi-momentum2.11. The distribution function
are scattered, changing their
band
number and quasi-momentum2.11. The distribution function
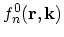 cannot change which means that the distribution of those electrons which contribute to band
cannot change which means that the distribution of those electrons which contribute to band 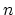 with quasi-momentum
with quasi-momentum
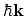 during the same time interval
during the same time interval 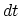 , must exactly offset for all the losses. This leads to the following expression:
, must exactly offset for all the losses. This leads to the following expression:
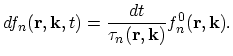 |
(2.38) |
This equation mathematically reflects the essence of the relaxation time approximation.
The number of electrons (2.36) in band 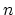 at time
at time 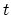 in the phase space domain
in the phase space domain
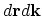 can be alternatively found selecting electrons
by the time of the last collision. Let
can be alternatively found selecting electrons
by the time of the last collision. Let
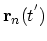 and
and
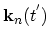 be the solutions of the semiclassical equations of motion,
(2.7) and (2.14), for band
be the solutions of the semiclassical equations of motion,
(2.7) and (2.14), for band 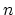 . Let this semiclassical trajectory pass through point
. Let this semiclassical trajectory pass through point
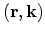 at time
at time 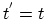 :
:
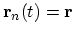 ,
,
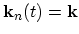 . If at time
. If at time 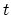 an electron was in the phase space domain
an electron was in the phase space domain
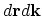 around
around
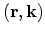 and had been scattered during the time interval
and had been scattered during the time interval
![$ [t^{'},t^{'}+dt^{'}]$](img246.png) , it must be scattered to the phase space domain
, it must be scattered to the phase space domain
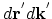 around
around
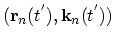 because after time
because after time 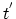 its trajectory is completely determined by the equations of motion. Using (2.38)
the total number of electrons scattered from point
its trajectory is completely determined by the equations of motion. Using (2.38)
the total number of electrons scattered from point
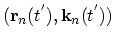 into the phase space domain
into the phase space domain
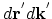 during
the time interval
during
the time interval
![$ [t^{'},t^{'}+dt^{'}]$](img246.png) can be written as:
can be written as:
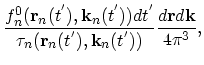 |
(2.39) |
where the conservation law of the phase space volume has been used, that is,
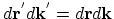 . Some of these electrons are not
scattered between time moments
. Some of these electrons are not
scattered between time moments 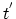 and
and 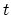 . Let the relative number of these electrons be
. Let the relative number of these electrons be
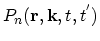 . Multiplying
(2.39) by
. Multiplying
(2.39) by
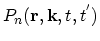 and summing over all possible values of
and summing over all possible values of 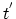 gives the expression for
gives the expression for 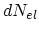 :
:
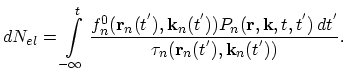 |
(2.40) |
Comparison with (2.36) gives for the non-equilibrium distribution function:
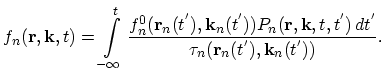 |
(2.41) |
The last expression clearly shows the structure of the non-equilibrium distribution function. The integrand includes the product of the total number of
electrons scattered between 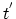 and
and
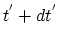 and moving in such a way that they reach the phase space domain
and moving in such a way that they reach the phase space domain
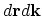 at time
at time 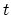 assuming that no scattering events have occurred and the relative number of electrons which really reach the phase space domain
assuming that no scattering events have occurred and the relative number of electrons which really reach the phase space domain
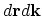 . The
contribution from all possible time moments is taken into account by the time integration.
. The
contribution from all possible time moments is taken into account by the time integration.
S. Smirnov:
![]() at time
at time ![]() in the phase space domain
in the phase space domain
![]() can be alternatively found selecting electrons
by the time of the last collision. Let
can be alternatively found selecting electrons
by the time of the last collision. Let
![]() and
and
![]() be the solutions of the semiclassical equations of motion,
(2.7) and (2.14), for band
be the solutions of the semiclassical equations of motion,
(2.7) and (2.14), for band ![]() . Let this semiclassical trajectory pass through point
. Let this semiclassical trajectory pass through point
![]() at time
at time ![]() :
:
![]() ,
,
![]() . If at time
. If at time ![]() an electron was in the phase space domain
an electron was in the phase space domain
![]() around
around
![]() and had been scattered during the time interval
and had been scattered during the time interval
![]() , it must be scattered to the phase space domain
, it must be scattered to the phase space domain
![]() around
around
![]() because after time
because after time ![]() its trajectory is completely determined by the equations of motion. Using (2.38)
the total number of electrons scattered from point
its trajectory is completely determined by the equations of motion. Using (2.38)
the total number of electrons scattered from point
![]() into the phase space domain
into the phase space domain
![]() during
the time interval
during
the time interval
![]() can be written as:
can be written as: