The time interval during which a closed subsystem is observed can be divided into a large number of equal intervals separated by times
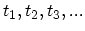 . At these moments the subsystem has corresponding phase space2.12 points
. At these moments the subsystem has corresponding phase space2.12 points
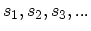 , which are distributed in the phase space with the
equilibrium distribution function2.13
, which are distributed in the phase space with the
equilibrium distribution function2.13
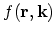 . The points
. The points
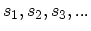 determine a
statistical ensemble at the initial time
determine a
statistical ensemble at the initial time 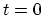 . The motion of the ensemble's phase space points is governed by the semiclassical equations of motion
containing coordinates and quasi-momenta of the subsystems only. At each time
. The motion of the ensemble's phase space points is governed by the semiclassical equations of motion
containing coordinates and quasi-momenta of the subsystems only. At each time 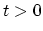 all the phase points are distributed according to the same
equilibrium distribution function. If the subsystem has
all the phase points are distributed according to the same
equilibrium distribution function. If the subsystem has 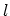 degrees of freedom, the motion can formally be considered as the stationary flow of a
"phase space gas" in the
degrees of freedom, the motion can formally be considered as the stationary flow of a
"phase space gas" in the 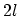 -dimensional phase space. This motion obeys a continuity equation2.14:
-dimensional phase space. This motion obeys a continuity equation2.14:
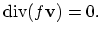 |
(2.42) |
In the case of the 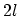 -dimensional phase space the last expression gives:
-dimensional phase space the last expression gives:
![$\displaystyle \sum_{i=1}^{l}\biggl[\Dot{r}_{i}\frac{\partial f}{\partial r_{i}}...
...ot{r}_{i}}{\partial r_{i}}+\frac{\partial\Dot{p}_{i}}{\partial p_{i}}\biggr]=0.$](img265.png) |
(2.43) |
The second term in this expression is equal to zero due to the semiclassical equations of motion2.15. The first term the total time derivative of the distribution function. Hence (2.43) is
reformulated as:
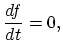 |
(2.44) |
where the differentiation is performed along the semiclassical phase space trajectories. This expression is called Liouville's theorem. From this theorem
it follows that the equilibrium distribution function can only be expressed through such mathematical functions of coordinates and quasi-momenta which are
conserved
during the motion of the closed subsystem. Such functions are called integrals of motion. Thus the equilibrium distribution function itself represents
an integral of motion.
As the equilibrium distribution function of two closed subsystems is equal to a product of the distribution functions of these subsystems (see
(2.25)), the logarithm of the distribution function represents an additive integral of motion. It is well known from mechanics that there
only exist seven independent integrals of motion. One of these integrals is the energy of a subsystem2.16. The dependence of the equilibrium distribution on the
energy has already been shown for fermions (2.30) and bosons (2.34).
S. Smirnov: