For two wave vectors 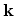 and
and
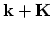 the solutions of Schrödinger equation (2.68) are related to each other as
the solutions of Schrödinger equation (2.68) are related to each other as
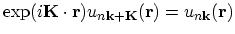 . This leads to equal eigenvalues
. This leads to equal eigenvalues
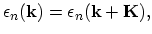 |
(2.70) |
and equal wave functions
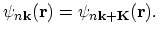 |
(2.71) |
It can be seen that each energy branch has the same period as the reciprocal lattice. As the functions
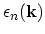 are periodic, they have
maxima and minima which determine the width of the bands.
are periodic, they have
maxima and minima which determine the width of the bands.
It should be noted that the wave vector 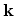 in (2.66) can always be chosen in a way to belong to the first Brillouin zone because any vector
in (2.66) can always be chosen in a way to belong to the first Brillouin zone because any vector
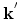 out of the first Brillouin zone can be represented as the sum
out of the first Brillouin zone can be represented as the sum
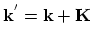 , where
, where 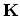 is a vector of the reciprocal
lattice. Using the equivalent form of Bloch's theorem:
is a vector of the reciprocal
lattice. Using the equivalent form of Bloch's theorem:
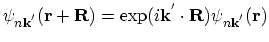 |
(2.72) |
together with (2.71) and the equality
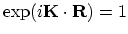 one obtains (2.72) for vector
one obtains (2.72) for vector 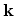 .
S. Smirnov:
.
S. Smirnov:
![]() in (2.66) can always be chosen in a way to belong to the first Brillouin zone because any vector
in (2.66) can always be chosen in a way to belong to the first Brillouin zone because any vector
![]() out of the first Brillouin zone can be represented as the sum
out of the first Brillouin zone can be represented as the sum
![]() , where
, where ![]() is a vector of the reciprocal
lattice. Using the equivalent form of Bloch's theorem:
is a vector of the reciprocal
lattice. Using the equivalent form of Bloch's theorem: