The plasmon concept arises from the consideration of an interacting electron gas described by the following Hamiltonian:
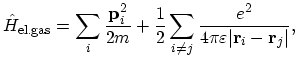 |
(2.125) |
where the first sum gives the kinetic energy and the second one arises from the Coulomb interaction between electrons. This Hamiltonian can be rewritten
using the random phase approximation [31,32,33,34] as follows:
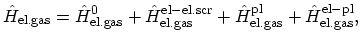 |
(2.126) |
where each contribution can be represented in the second quantized form [35]. The first term
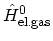 is the kinetic
energy of the electron gas:
is the kinetic
energy of the electron gas:
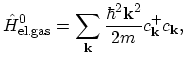 |
(2.127) |
where
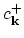 and
and
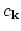 are the electron creation and annihilation operators, respectively, and spherical and parabolic dispersion is
assumed.
are the electron creation and annihilation operators, respectively, and spherical and parabolic dispersion is
assumed.
The second term
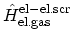 gives the contribution from a two-electron screened Coulomb interaction:
gives the contribution from a two-electron screened Coulomb interaction:
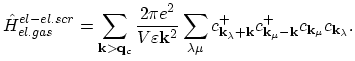 |
(2.128) |
As can be seen, this term accounts for scattering of two electrons with the initial quasi-momenta
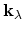 and
and
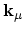 and the final
quasi-momenta
and the final
quasi-momenta
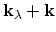 and
and
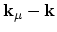 respectively. Screening is taken into account through the cut-off wave vector
respectively. Screening is taken into account through the cut-off wave vector
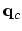 which separates short- and long-range parts of the Coulombic term.
which separates short- and long-range parts of the Coulombic term.
The third term
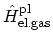 describes a non-interacting plasmon gas, that is, the quantized oscillations of the electron
gas2.34:
describes a non-interacting plasmon gas, that is, the quantized oscillations of the electron
gas2.34:
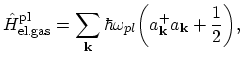 |
(2.129) |
where
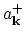 ,
,
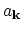 are the plasmon creation and annihilation operators and
are the plasmon creation and annihilation operators and
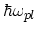 is the plasmon energy.
is the plasmon energy.
The forth term
 represents the electron-plasmon interaction:
represents the electron-plasmon interaction:
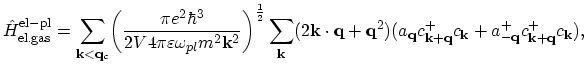 |
(2.130) |
where two terms in the second sum can conveniently be treated in terms of absorption and emission of a plasmon in the same way as it has been shown above
for phonons.
The possible plasmon-phonon coupling [36,37,38] is not considered in this work as it plays an important role only in polar
semiconductors where in the degenerate case the frequencies of the charge density fluctuations are comparable to the optical frequencies.
S. Smirnov:
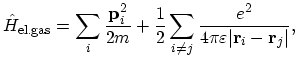
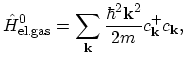
![]() gives the contribution from a two-electron screened Coulomb interaction:
gives the contribution from a two-electron screened Coulomb interaction:
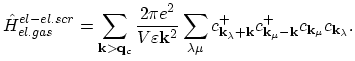
![]() describes a non-interacting plasmon gas, that is, the quantized oscillations of the electron
gas2.34:
describes a non-interacting plasmon gas, that is, the quantized oscillations of the electron
gas2.34:
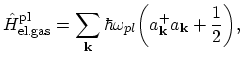
![]() represents the electron-plasmon interaction:
represents the electron-plasmon interaction: