The energy splitting and the hydrostatic shift of the mean energy depend on the orientation of the applied forces.
The interface coordinate system is specified as a system with its 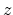 -axis perpendicular to the hetero-interface. The form of the strain tensor
-axis perpendicular to the hetero-interface. The form of the strain tensor
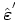 in this coordinate system can be found as follows.
in this coordinate system can be found as follows.
The condition of biaxial dilatation or contraction gives:
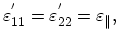 |
(3.32) |
where
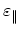 is the in-plane strain given as the relative lattice mismatch:
is the in-plane strain given as the relative lattice mismatch:
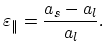 |
(3.33) |
Here 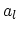 is the lattice constant of the layer and
is the lattice constant of the layer and 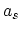 that of the substrate. The substrate is assumed to be thick enough to remain unstrained.
Further, the condition of vanishing in-plane shear implies:
that of the substrate. The substrate is assumed to be thick enough to remain unstrained.
Further, the condition of vanishing in-plane shear implies:
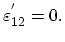 |
(3.34) |
It is also assumed that there is no any film distortion which means the following conditions:
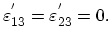 |
(3.35) |
This is justified for the case of substrates with high rotational symmetry. In other cases it is relatively weak for SiGe structures.
Thus under these conditions the strain tensor for the SiGe active layer is diagonal in the interface coordinate system. The two diagonal elements
are known to be equal to
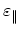 . To determine the third diagonal element Hooke's law is applied. It linearly relates the components of
the stress and the strain tensors
. To determine the third diagonal element Hooke's law is applied. It linearly relates the components of
the stress and the strain tensors
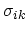 and
and
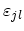 :
:
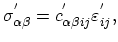 |
(3.36) |
where 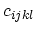 is a tensor of rank four called the elastic stiffness tensor. As the only external stress is in-plane, the out-of-plane component
vanishes
is a tensor of rank four called the elastic stiffness tensor. As the only external stress is in-plane, the out-of-plane component
vanishes
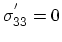 |
(3.37) |
which gives for the third diagonal component of the strain tensor:
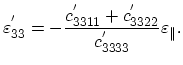 |
(3.38) |
S. Smirnov:
![]() -axis perpendicular to the hetero-interface. The form of the strain tensor
-axis perpendicular to the hetero-interface. The form of the strain tensor
![]() in this coordinate system can be found as follows.
in this coordinate system can be found as follows.
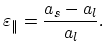
![]() . To determine the third diagonal element Hooke's law is applied. It linearly relates the components of
the stress and the strain tensors
. To determine the third diagonal element Hooke's law is applied. It linearly relates the components of
the stress and the strain tensors
![]() and
and
![]() :
: