Next: 2. 3. 2 Incidence and Traversal Up: 2. 3 Topological Structures Previous: 2. 3 Topological Structures
For the definition of the underlying topological structure the definition of a topological space is used [64]. A topological space consists of a base set
![]() as well as a topology
as well as a topology
![]() which is a set of subsets of
which is a set of subsets of
![]() . The topology contains the empty set
. The topology contains the empty set ![]() and the base set
and the base set
![]() . Furthermore, the intersection of a finite number of elements of the topology as well as the union of an arbitrary number of elements of the topology is contained in the topology. The definition can be formalized in the following manner [64] and is called the open set definition of a topological space:
. Furthermore, the intersection of a finite number of elements of the topology as well as the union of an arbitrary number of elements of the topology is contained in the topology. The definition can be formalized in the following manner [64] and is called the open set definition of a topological space:
| (2.14) | |||
| (2.15) | |||
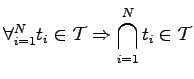 |
(2.16) | ||
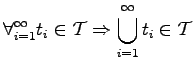 |
(2.17) |
First, it has to be stated that the number of possible sets within the topological space has to be finite due to the limitations of the computer when associatively storing coefficients on the elements. Secondly, in most cases the use of sets is cumbersome, because one is actually interested in single elements of the tesselation, whereas sets containing different unconnected elements of the tesselation are rather seldomly used. In analogy with vector spaces, one can find a basis of elements from which the topological space can be composed using union operations.
A set of subsets of a set
![]() on which a topological space
on which a topological space
![]() is formed is called a basis, if each set contained in the topology can be written as
is formed is called a basis, if each set contained in the topology can be written as
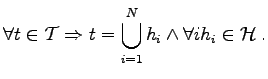 |
(2.18) |
However, each set which is an element of the tesselation is the result of an intersection of (a finite number of) such elements. If the underlying topological space is derived from a finite cell complex which usually results from a tesselation, the basis of the respective space contains all open cells, edges, faces, and vertices (or points).
If the information about the cells and their mutual intersection and union operations is available, the information of the elements of lower dimension can be obtained by intersection of the (closed) cells. The set of the closed cells is said to form a subbasis, namely a set from which all elements of the topological space
![]() can be obtained by a union of arbitrarily (but finitely) many sets of the subbasis
can be obtained by a union of arbitrarily (but finitely) many sets of the subbasis
![]() .
.
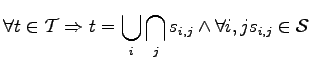 |
(2.19) |
The main advantage of such a subbasis is that there is only the restriction that
![]() for the subbasis
for the subbasis
![]() . (when using a finite number of elements).
. (when using a finite number of elements).
In order to specify the construction of the topological space, the notion of a CW complex is introduced [64]. A CW complex is a structure which additionally fulfills the so-called weak-topology property. This means, that the boundary of each element of dimension ![]() is formed by one or more elements of the dimension
is formed by one or more elements of the dimension ![]() . As a consequence, an
. As a consequence, an ![]() -dimensional complex consists of at least one element for each dimension
-dimensional complex consists of at least one element for each dimension
![]() .
.
The second property which has to be fulfilled by a CW complex, namely the closure-finiteness, is trivially fulfilled by finite cell complexes which are directly implied by the use of a computer.
Michael 2008-01-16