Next: 3. 1. 2 Re-Formulation on Topological Properties Up: 3. 1 Finite Element Schemes Previous: 3. 1 Finite Element Schemes
The method is based on the notion of the weak formulation or weak solution, which is defined in the following manner: A function ![]() is a weak solution of a differential equation
is a weak solution of a differential equation
![]() within the domain
within the domain
![]() , iff for each function
, iff for each function ![]() the following condition holds true:
the following condition holds true:
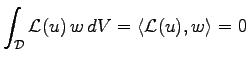 |
(3.1) |
A widely used approach, which uses the shape functions as weighting functions is the Galerkin approach. It has been shown that such an approach has many advantages such as providing a symmetric equation system or system matrix.
The typical formulation of a differential equation using the Galerkin finite element method is written as
Michael 2008-01-16