Next: 3. 4. 2 Topological Neighborhood Considerations Up: 3. 4 Finite Difference Schemes Previous: 3. 4 Finite Difference Schemes
Again, the Laplace operator is considered for the specification of a finite difference scheme. A typical formula for a finite difference scheme may have the following shape:
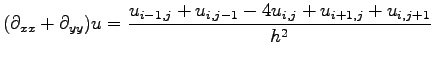 |
(3.51) |
If the distance between two neighboring vertices, here denoted as ![]() is equal for all vertices, independently from the direction, the formulae can be written in a very simple manner. Otherwise, the distance between the single vertices has to be calculated separately either by using the length of the edges or alternatively by explicitly using the vertex coordinates.
is equal for all vertices, independently from the direction, the formulae can be written in a very simple manner. Otherwise, the distance between the single vertices has to be calculated separately either by using the length of the edges or alternatively by explicitly using the vertex coordinates.
Michael 2008-01-16