Next: 4. 1. 2 Constants Up: 4. 1 Line-Wise Assembly Previous: 4. 1 Line-Wise Assembly
One equation, comprising a matrix line and one right-hand-side vector entry is considered a mathematical entity. It can be viewed as an equation which depends on a number of unknown variables on which the equation linearly depends.
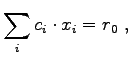 |
(4.1) |
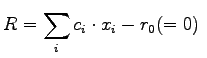 |
(4.2) |
| (4.3) |
It can be seen easily that the application of arbitrary functions on linear expressions does not necessarily lead to linearized expressions. Only very few operations (i.e. linear operations) preserve the algebraic structure of a linear equation. This especially holds true for addition and scalar multiplication by which an affine linear algebra is created. Of course, in general, especially when solving non-linear equations such an algebraic structure cannot be preserved.
This problem can be easily fixed, if after each nonlinear operation a subsequent linearization step is performed. It can be shown easily that the number of intermediate linearization steps is not relevant as long as removable discontinuities are avoided.
In the following sections the basic operations are shown. As an example, the method is demonstrated on a simple nonlinear discretized differential equation system. Afterwards the assembly of the system matrix is shown. In a second example, the same calculations are carried out for an eigenvalue equation system.
Michael 2008-01-16