Firstly, basic linear operations such as addition and inversion are discussed. These operations directly lead to linear expressions and do not require subsequent linearization. According to the linearity of the operations, addition, subtraction, and negation are applied in the following manner:
If the multiplication of two linearized expressions is performed, higher order terms consisting of bilinear expressions are neglected and truncated.
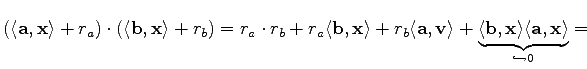 |
|
|
|
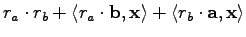 |
|
|
(4.7) |
Functions can be applied to a linearized expression as follows. First, the function as well as its derivative have to be known. This function is denoted as 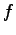 , its derivative is referred to as
, its derivative is referred to as 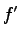 . The application of the function on the linearized expression yields
. The application of the function on the linearized expression yields
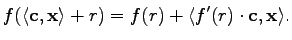 |
(4.8) |
The verification can be easily performed by using the chain rule of differentiation. Furthermore, it has to be mentioned that division can be considered a binary function, the application of which on linearized expressions is straight forward. However, it has to be mentioned, that the occurrence of solution variables as divisors is often avoided by proper multiplication.
In the following a linearized expression will be written shortly as follows:
![$\displaystyle \langle \mathbf{c}, \mathbf{x} \rangle + r =: [c_1, c_2, \ldots, c_n ; r]$](img440.png) |
(4.9) |
Accordingly, the rules for addition, multiplication, and function application are written as
If two linearized expressions are divided, the case might occur that both, numerator and denominator are identically zero and Bernoulli's (del Hospital's) rule has to be applied to obtain the correct result. This is numerically unstable and accordingly leads to various problems regarding the evaluation of the quotient rule of differentiation. Inserting the values leads to divisions by zero or - even worse - to a division by a very small floating point number. Furthermore, for the correct evaluation of the fully linearized result comprising the coefficients for the variables, higher order terms (which are not available then) of the linearized expressions has to be considered.
For this reason, a critical function with a removable discontinuity, for instance
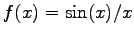 is implemented with a Taylor series expansion in order to avoid the division. The application of the function
is implemented with a Taylor series expansion in order to avoid the division. The application of the function 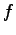 does not cause problems because the function as well as its derivative are continuous and can be determined in a straight forward manner.
does not cause problems because the function as well as its derivative are continuous and can be determined in a straight forward manner.
Michael
2008-01-16
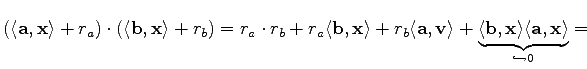
![]() is implemented with a Taylor series expansion in order to avoid the division. The application of the function
is implemented with a Taylor series expansion in order to avoid the division. The application of the function ![]() does not cause problems because the function as well as its derivative are continuous and can be determined in a straight forward manner.
does not cause problems because the function as well as its derivative are continuous and can be determined in a straight forward manner.