Next: 4. 4 Solution of Algebraic Problems Up: 4. 3 Boundaries and Interfaces Previous: 4. 3. 1 Boundary Conditions
Interfaces and especially triple points, namely points which are at the intersection of three or more regions of different governing equations are problematic for many programming environments. Problems occur when the simulation domain is initially segmented and the equations are assembled for the single topological elements for each segment separately.
In such a case it is very cumbersome to fill in the respective matrix entries into a common system matrix and manage the couplings between single interface points of different segments which coincide. In [83] methods are shown which are numerically stable for combining two system matrices each of which is the result of discretizing segments with a common boundary.
The line-wise assembly method using underlying segmentation and incidence information provides proper means for the specification of the governing equations of an interface point or a point incident to three segments, namely a triple point. For instance, for a triple point the finite volume discretization the divergence of the flux ![]() is set zero.
is set zero.
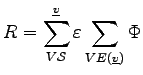 |
(4.44) |
Michael 2008-01-16