Next: 3. 4. 4 Conclusion Up: 3. 4 Finite Difference Schemes Previous: 3. 4. 2 Topological Neighborhood Considerations
In the special case of the Laplace operator the vector
![]() has the following form
has the following form
| (3.60) |
For a grid with a regular distance ![]() between neighboring vertices, the geometrical coefficient matrix
between neighboring vertices, the geometrical coefficient matrix
![]() yields for five and nine neighboring points:
yields for five and nine neighboring points:
![$\displaystyle \mathcal{G}_5 =
\left[
\begin{array}{c c c c c}
1 & 0 & 0 & 0 & 0...
...2 & 0 \\
1 & 0 & h & 0 & h^2/2 \\
1 & 0 & -h & 0 & h^2/2
\end{array}\right]
$](img401.png)
![\begin{displaymath}
\mathcal{G}_9 =
\left[
\begin{array}{c c c c c c c c c}
1& ...
... &-2h& 0 & h^2 & 0 & -3h^3/2 & 0 & 8h^4/3
\end{array}\right]
\end{displaymath}](img402.png)
After eliminating derivatives which do not appear in the series expansion of the single points, the matrices can be re-written. The derivative vector
![]() is written as:
is written as:
| (3.61) |
The vector
![]() is reduced to the following form:
is reduced to the following form:
| (3.62) |
Inserting into the formula (3.58) yields the well known expressions. The function
![]() can be written as
can be written as
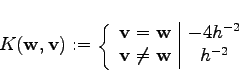
For nine points the following formula is obtained:
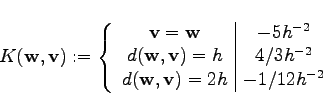
Michael 2008-01-16