Energy Dispersion of the Conduction Band Minimum of Strained Si: Method 2
The above formulae have been derived, assuming that the conduction band minima
are located at
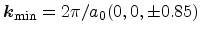 , which is a
good approximation only for small shear strain. As can be seen from
Figure 3.12 the minimum of the conduction band is expected to move
towards the
, which is a
good approximation only for small shear strain. As can be seen from
Figure 3.12 the minimum of the conduction band is expected to move
towards the 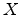 point
as the strain-induced splitting between the conduction band becomes larger. As
a direct consequence, the conduction bands shape is deformed and the previous
assumption
point
as the strain-induced splitting between the conduction band becomes larger. As
a direct consequence, the conduction bands shape is deformed and the previous
assumption
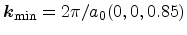 is not satisfied.
is not satisfied.
Thus, a more general model for the effect of shear strain on the effective
masses needs to be developed, which takes the movement of the conduction band
minimum as a function of strain into account. The effective masses are
subsequently evaluated at the position of the conduction band minimum
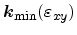 .
.
The position of the minimum can be found from (3.73) by setting
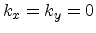 :
:
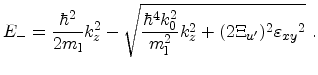 |
(3.90) |
Here, relations (3.75) and (3.77) are used to replace 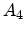 and
and 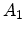 , and
, and 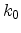 denotes the position of the unstrained conduction band
minimum measured from the zone boundary
denotes the position of the unstrained conduction band
minimum measured from the zone boundary 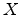 ,
,
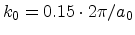 . Setting
. Setting
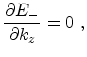 |
(3.91) |
the position of the conduction band minimum
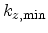 can be
obtained
can be
obtained
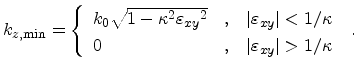 |
(3.92) |
It can be seen that for strain smaller in magnitude than 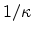 , the minimum position
is shifted towards the
, the minimum position
is shifted towards the  point. For
point. For
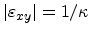 , the position
of the minimum is located at the
, the position
of the minimum is located at the 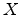 point, thus
point, thus
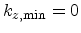 . The
position is fixed, even when
. The
position is fixed, even when
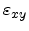 is further increased. The changing
position of
is further increased. The changing
position of
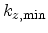 is visualized in Figure 3.12, where
the impact of shear strain on the shape of the conduction bands
is visualized in Figure 3.12, where
the impact of shear strain on the shape of the conduction bands 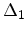 and
and
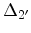 is plotted.
is plotted.
The strain dependent longitudinal mass
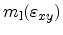 can be obtained from
(3.73) by calculating
can be obtained from
(3.73) by calculating
 |
(3.93) |
The following expressions can be derived after some algebraic manipulations
Similar to (3.92), the dependence of the longitudinal mass on strain is
described by two expressions, depending on whether the magnitude of strain is
smaller or bigger than 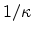 . Note that in the approximation of
Section 3.7.2 the effect of shear strain was modeled by the expansion
(3.76) about the conduction band minimum of the unstrained lattice,
such that the longitudinal mass
. Note that in the approximation of
Section 3.7.2 the effect of shear strain was modeled by the expansion
(3.76) about the conduction band minimum of the unstrained lattice,
such that the longitudinal mass
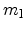 is not influenced by strain.
is not influenced by strain.
To derive the transverse effective masses that include the dependence
on
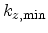 , first (3.73) is transformed to the
rotated coordinate system introduced in (3.85).
, first (3.73) is transformed to the
rotated coordinate system introduced in (3.85).
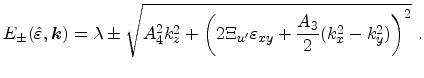 |
(3.95) |
The effective mass in the ![$ x'=[110]$](img590.png) and
and
![$ y'=[1\bar{1}0]$](img591.png) direction can be obtained from
direction can be obtained from
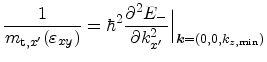 |
(3.96) |
and
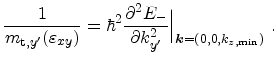 |
(3.97) |
The strain dependence of the transverse masses is given by
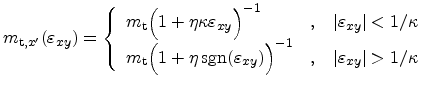 |
(3.98) |
for the [110] direction and by
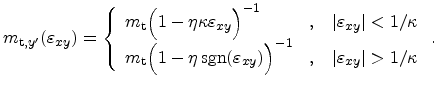 |
(3.99) |
for the
![$ [1\bar{1}0]$](img596.png) direction. Here,
direction. Here,
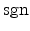 denotes the signum
function. For
denotes the signum
function. For
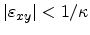 the effective masses derived in this way
are consistent with equations (3.87) and
(3.88). However, for
the effective masses derived in this way
are consistent with equations (3.87) and
(3.88). However, for
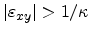 the transverse masses
are constant and depend on the sign of the strain only.
the transverse masses
are constant and depend on the sign of the strain only.
Finally, an analytical expression for the valley shift induced by shear strain
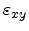 , which was given in Section 3.6.2, is calculated. According to
(3.92), equation (3.90) has to be evaluated at
, which was given in Section 3.6.2, is calculated. According to
(3.92), equation (3.90) has to be evaluated at
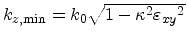 for
for
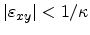 . For
. For
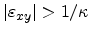 the energy shift at the
the energy shift at the 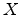 point
determines the overall valley shift. The shift between the valley pair along
[001] and the valley pairs along [100] or [010] is obtained from
point
determines the overall valley shift. The shift between the valley pair along
[001] and the valley pairs along [100] or [010] is obtained from
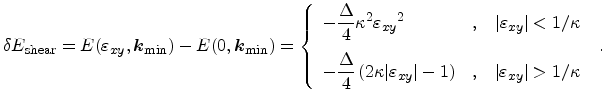 |
(3.100) |
This derivation shows that the valley splitting cannot be obtained if the
spectrum of the strained crystal is expanded around the conduction band
minimum 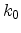 of the unstrained crystal, as it was assumed in
Section 3.7.2.
of the unstrained crystal, as it was assumed in
Section 3.7.2.
Figure 3.13:
Constant energy ellipsoids for the Si
conduction band with
 (left side) and
(left side) and
 (right
side). In unstrained Si there are six equivalent valleys along the three
principal axes. In the deformed lattice the valleys along
(right
side). In unstrained Si there are six equivalent valleys along the three
principal axes. In the deformed lattice the valleys along
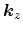 go down
in energy, hence the surface of constant energy is bigger. The constant energy
lines in the
go down
in energy, hence the surface of constant energy is bigger. The constant energy
lines in the
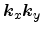 -plane are characterized by two masses,
-plane are characterized by two masses,
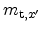 and
and
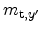 .
.
|
|
E. Ungersboeck: Advanced Modelling Aspects of Modern Strained CMOS Technology
![]() , which is a
good approximation only for small shear strain. As can be seen from
Figure 3.12 the minimum of the conduction band is expected to move
towards the
, which is a
good approximation only for small shear strain. As can be seen from
Figure 3.12 the minimum of the conduction band is expected to move
towards the ![]() point
as the strain-induced splitting between the conduction band becomes larger. As
a direct consequence, the conduction bands shape is deformed and the previous
assumption
point
as the strain-induced splitting between the conduction band becomes larger. As
a direct consequence, the conduction bands shape is deformed and the previous
assumption
![]() is not satisfied.
is not satisfied.
![]() .
.
![]() :
:
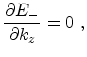
![]() can be obtained from
(3.73) by calculating
can be obtained from
(3.73) by calculating

![]() , first (3.73) is transformed to the
rotated coordinate system introduced in (3.85).
, first (3.73) is transformed to the
rotated coordinate system introduced in (3.85).
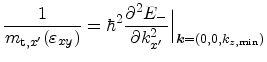
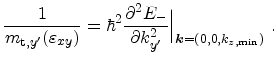
![]() , which was given in Section 3.6.2, is calculated. According to
(3.92), equation (3.90) has to be evaluated at
, which was given in Section 3.6.2, is calculated. According to
(3.92), equation (3.90) has to be evaluated at
![]() for
for
![]() . For
. For
![]() the energy shift at the
the energy shift at the ![]() point
determines the overall valley shift. The shift between the valley pair along
[001] and the valley pairs along [100] or [010] is obtained from
point
determines the overall valley shift. The shift between the valley pair along
[001] and the valley pairs along [100] or [010] is obtained from
![\includegraphics[scale=1.0, clip]{inkscape/bzEleStress110.eps}](img606.png)