D I S S E R T A T I O N
Hydrogen Related Defects in Amorphous SiO2 and the Negative Bias Temperature Instability
ausgeführt zum Zwecke der Erlangung des akademischen Grades
eines Doktors der technischen Wissenschaften
unter der Leitung von
Ao.Univ.Prof. Dipl.-Ing. Dr.techn. Tibor GRASSER
Institut für Mikroelektronik
eingereicht an der Technischen Universität Wien
Fakultät für Elektrotechnik und Informationstechnik
von
Dipl.-Ing. Yannick WIMMER
00425457 / E 786 710
Herminengasse 6/12, 1020 Wien
Wien, im November 2017
Abstract
The bias temperature instability (BTI) is a serious reliability concern in metal-oxide-semiconductor field-effect transistors (MOSFETs). It is observed when a large voltage is applied to the gate contact of the MOSFET while all other terminals are grounded. Furthermore, the effect is more pronounced at elevated temperatures. In silicon-based devices BTI is considerably stronger when a
negative bias voltage is applied to a MOSFET, which is referred to as negative BTI (NBTI). Its counterpart for positive bias is referred to as PBTI. It is suspected that both effects arise from a similar
fundamental origin. Even though BTI was described for the first time over half a century ago, its underlying cause is still disputed. The effect is suspected to be caused by point-defects in the oxide which are able to capture and emit charges under operating conditions.
The present work focuses on NBTI in silicon (Si) based devices using silicon dioxide () as gate oxide.
Due to the continuous downsizing, devices have reached dimensions where they merely contain very few defects each, which, during the last years, has enabled the study of the electric response of single defects in experiments. Research indicates that NBTI consists of two components dominantly contributing to the device degradation. In measurements, the signal often does not recover fully to the initial “unstressed” level. One, therefore, distinguishes between the recoverable component (RC) and a more or less permanent component (PC). Theoretical models have been previously developed for both components. These models are presented in this work and are subsequently used as a basis for the investigations performed in this thesis. The parameters of the models can be determined by measurements, but the same parameters can also be theoretically calculated for several defect candidates. For the theoretical calculations, density functional theory (DFT) is used. A comparison of the obtained data is used to judge whether a suggested defect candidate is suitable to explain NBTI.
Because of the gate oxide not being crystalline but rather amorphous, an additional layer of complexity is added. This results in a broad distribution of parameters, consistent with the
measurements. In order to obtain theoretical defect parameter distributions to compare with, a large number of DFT calculations has to be performed in different amorphous structures, consuming considerable computational resources. In this work, the results of such calculations for the three most promising defect candidates – the oxygen vacancy (OV), the hydrogen bridge (HB) and the hydroxyl-E (H-E
) center – are
presented.
The present work focuses on narrowing down the possible number of defect candidates for NBTI. It also addresses an additional feature observed in measurements, the so-called volatility (defects frequently disappearing and reappearing in the
measurements). A possible explanation for this effect involves hydrogen atoms relocating within the oxide, which has led to a more detailed investigation of hydrogen migration barriers in in this work. Lastly, all the mentioned models rely on
the concept of potential energy surfaces (PESs), which describe the energy of a system of atoms in terms of their position. The PESs are usually assumed to be of a parabolic shape around the energy
minimum, which is subjected to a closer examination in this work. There follow possible explanations for the experimentally observed double charge capture and emission processes. The results of this work provide a better
understanding of the parameters needed for the models describing the recoverable and permanent component of NBTI, also giving
new insights into the possible interlink of the two models.
Kurzfassung
Die Bias Temperatur Instabilität (BTI) ist ein gravierendes Zuverlässigkeitsproblem in Metall-Oxid-Halbleiter-Feldeffekttransistoren (MOSFETs). BTI tritt auf, wenn eine verhältnismäßig hohe Spannung am Gate-Kontakt des Transistors angelegt wird, während die
anderen Kontakte geerdet bleiben. Weiters ist BTI stark temperaturabhängig. In Silizium-basierten MOSFETS ist der Effekt größer, wenn eine negative Spannung an einen MOSFET angelegt wird. Dies wird als negative BTI (NBTI) bezeichnet, das Gegenstück für
positive Spannung, PBTI. Es wird vermutet, dass beide Effekte von denselben grundlegenden physikalischen Ursachen herrühren. Obwohl die erste Beschreibung von BTI bereits über ein halbes Jahrhundert zurückliegt, ist aber der fundamentale Auslöser immer noch
umstritten. Es wird angenommen, dass der Effekt von Punktdefekten im Oxid verursacht wird, welche in der Lage sind, Ladungsträger einzufangen und zu emittieren. Die vorliegende Arbeit konzentriert sich auf NBTI in Silizium (Si) basierten Bauelementen mit
Siliziumdioxid als Gate-Oxid.
Aufgrund der fortschreitenden Miniaturisierung haben elektronische Bauelemente mittlerweile so kleine Dimensionen erreicht, dass in jedem MOSFET nur mehr einige wenige Defekte zu finden sind. Daher ist es seit einigen Jahren möglich, den Einfluss einzelner Defekte in Experimenten aufzulösen. Die Forschungsergebnisse zeigen, dass NBTI aus zwei Komponenten besteht, welche wesentlich zur Degradation beitragen. Am Ende einer Messung erreicht das Messsignal oft nicht mehr den ursprünglichen Wert. Daher wird zwischen einer ausheilbaren (recoverable) Komponente und einer permanenten Komponente unterschieden. Für beide wurden bereits theoretische Modelle entwickelt, welche in dieser Arbeit präsentiert werden und als Basis für weiter führende Untersuchungen dienen. Die Parameter dieser Modelle können einerseits aus Experimenten abgeleitet werden, andererseits aber auch für verschiedene Defekt-Kandidaten theoretisch berechnet werden. Zur Berechnung grundlegender Eigenschaften und Parameter dieser Defekte wurde die Dichtefunktionaltheorie (DFT) verwendet. Ein Vergleich zwischen den experimentell und theoretisch gewonnenen Parametern kann somit verwendet werden, um festzustellen, ob ein Defekt-Kandidat potenziell in der Lage ist, NBTI zu verursachen.
Der Umstand, dass das Gate-Oxid nicht kristallin ist, sondern eine amorphe Struktur aufweist, verkompliziert diese Untersuchungen zusätzlich. Sowohl die berechneten als auch die experimentell abgeleiteten Parameter weisen eine breite Verteilung auf. Um die
mittels DFT simulierten Parameter mit experimentellen Werten und Verteilungen vergleichen zu können, ist eine große Zahl von Berechnungen in unterschiedlichen amorphen Strukturen nötig. Dafür werden viel Rechenzeit und leistungsstarke Computercluster benötigt.
In dieser Arbeit werden die Ergebnisse für die drei vielversprechendsten Defekt-Kandidaten – die Sauerstoffvakanz, die Wasserstoffbrücke und das sogenannte hydroxyl-E center – präsentiert.
Der Schwerpunkt der vorliegenden Arbeit liegt darauf, die Anzahl der möglichen Defekt-Kandiaten für NBTI einzugrenzen. Darüber hinaus werden weitere, experimentell verifizierte und mit Punktdefekten in Zusammenhang stehende, Effekte behandelt. Zum Beispiel das wiederholte Verschwinden und Wiedererscheinen von Defekten in den Messungen, ein Effekt, der als volatility bezeichnet wird. Eine mögliche Erklärung hierfür wäre, dass sich Wasserstoffatome im Oxid verlagern. Aus diesem Grund wurden auch die generellen theoretischen Migrationsbarrieren für Wasserstoff einer genaueren Untersuchung unterzogen. Zuletzt wird noch eine verbreitete Annahme für die Potentialhyperflächen (PESs) näher untersucht. Die PESs beschreiben die Energie eines Systems, basierend auf den Positionen jedes Atoms. Typischerweise wird für sie eine parabolische Näherung rund um das Energieminimum verwendet. Diese Approximation wird einer genaueren Prüfung unterzogen. Durch eine detaillierte Beschreibung der PEs ergeben sich mögliche Erklärungen für die experimentell beobachteten doppelten Ladungseinfänge oder Emissionen. Die Ergebnisse der vorliegenden Arbeit bieten ein besseres Verständnis der dem NBTI Effekt zugeschriebenen Punktdefekte. Weiters ergeben sich dadurch mögliche Zusammenhänge zwischen der ausheilbaren (recovarable) und der permanenten NBTI-Komponente.
Acknowledgements
This thesis owes its existence to a very large number of people to whom I would like to offer my heartfelt appreciation. Therefore, firstly I would like to thank all those who took part in this endeavor, but who I unforgivably forgot to mention by name when writing up the following lines: I’m truly sorry. Secondly, I want to thank my high school physics teacher Prof. Heimel for providing me with the certainty that studying physics is the path to pursue.
Foremost, I want to express my deep gratitude to my advisor Tibor Grasser for providing his guidance and support throughout the years. His scientific commitment, fascination for the research field and demand for scientific accuracy and precision surely are an inspiration for many students. For the perfect working environment at the Institute for Microelectronics, credit goes to Erasmus Langer, Siegfried Selberherr, Tibor Grasser, Renate Winkler, Diana Pop, Ewald Haslinger and Manfred Katterbauer. Thank you for the truly great ambiance at our Institute.
My special thanks goes out to all my colleagues for so many things, including fruitful discussions, help with programming or Latex struggles, the groundbreaking work my thesis is based on, being travel companions, being my beloved roommates, lunchtime companions and of course for the proofreading of papers and of this thesis, etc. I want to thank Markus Bina, Johann Cervenka, Tassem El-Sayed, Wolfgang Gös, Alexander Grill, Markus Jech, Markus Kampl, Theresia Knobloch, Mahdi Moradinasab, Florian Rudolf, Karl Rupp, Gerhard Rzepa, Franz Schanovsky, Prateek Sharma, Alex Shluger, Zlatan Stanojevic, Oliver Triebl, Stanislav Tyaginov, Bianka Ullmann, Michael Waltl, Dominic Waldhör and Stefanie Wolf.
Speaking of lunchtime, I should not forget to thank the team of “Fein Essen”, my food base-camp during the last years. It really is an improvement of the quality of life to have a place like that near your workspace.
Throughout the last years, the team of the Vienna Scientific Cluster was providing and maintaining three different supercomputers, without which this thesis would not have been possible. Especially I would like to thank Markus Stöhr for his help with compiling several different versions of the CP2K code on the different clusters.
I also would like to take this opportunity to thank all my colleagues and friends who accompanied and supported, inspired (and partly also dragged me) throughout my physics degree course, during which many long-lasting friendships were formed.
Of course, I want to thank my family who, in spite of certain strokes of fate, supported and encouraged me throughout my studies. Thank you to my mother Eva Maria, my brother Kevin and my aunt Helga for providing all the preconditions for pursuing my interests. Here if anywhere I also want to express my gratitude to all the family members who supported me, who are no longer with us to witness the completion of this work.
Finally, a very special thanks to my girlfriend Julia for her patience, support in the last months, not to forget her proofreading skills. Moreover, I can not appreciate enough that she seems to find nearly all my little follies adorable. Thank you!
Contents
List of Figures
1 Introduction
Point defects in solids have a large influence on the macroscopic properties (mechanical, electrical, optical, etc.) of the host material. A point defect occurs only at or around a single lattice point and is not extended in space in any dimension. Semiconductor technology itself is largely based on the intentional introduction of impurities into a host material , the so-called doping. A doped semiconductor contains a relatively low concentration of point defects, with either one electron more or one electron less than the host material, thereby completely altering its electronic properties. However, also many detrimental effects in semiconductor devices are associated with point defects. Although it is widely accepted that these effects are caused by trapping and release of electrons and holes by such defects [1–3], their detailed microscopic nature remains unknown. Therefore, a better understanding of these processes is of utmost importance in the field. This thesis focuses predominantly on the mechanisms related to the bias temperature instability (BTI) [4–7] in silicon (Si) based metal-oxide-semiconductor field-effect transistors (MOSFETs), more precisely on the negative bias temperature instability (NBTI). The findings also give new insights into possible underlying mechanisms of other effects.
1.1 Detrimental Effects in MOSFETs
The performance of MOSFETs is affected by a number of detrimental factors, such as random telegraph noise (RTN) [1, 8], 1/f noise [9], hot-carrier degradation (HCD) [10–13], time-dependent dielectric breakdown [14, 15] and bias temperature instability (BTI) [4–7]. All these effects have been known and explored for many decades, and have been linked to defects in the gate oxide trapping charges [1–3]. Nevertheless, the exact underlying physical mechanisms remain controversial [16, 17].
Oxide defects in MOSFETs can be charged and discharged when the trap level of a defect is moved across the respective Fermi-level of the channel or gate. In electronic devices, this happens when a certain stress-voltage (bias) is applied across the oxide of a device. The charge capture and emission time constants of such oxide defects are typically distributed over many orders of magnitude, from nano to several kilo-seconds (and presumably even more, since our measurement window is limited to these timescales) [1, 3, 18].
During the past years, the devices have been scaled down continuously and have reached nanometer dimensions [19]. In larger devices, it was only possible to observe a large number of defects simultaneously [1, 20, 21]. Due to the continuous downsizing, devices have reached dimensions where they merely contain very few defects each. On the one hand, this has aggravated the impact of single defects on the device behavior, where just a few defects dominate the degradation [3, 22–25, YWC1]. The so-called variability (the stochastic performance variations between devices of the same kind) is, therefore, more pronounced in smaller devices. On the other hand, the possibility of measuring the electric response of single defects has led to the development of new experimental methods for probing individual defect properties. Using small area devices, one can clearly and unambiguously identify and characterize individual defects responsible for the macroscopically measurable degradation [YWJ1], giving new insight into the charge capture and emission dynamics of single defects.
1.1.1 The Bias Temperature Instability
BTI is usually encountered in MOS devices when voltage is supplied to the gate contact (up to 10 MV/cm oxide field) while all other terminals stay grounded [26–28].
This is the main difference between BTI and HCD where a voltage is additionally applied to the drain contact. Thus, under HCD conditions high energetic carriers are present [10–13], which are absent
under BTI conditions. However, it should be pointed out that depending on the operating conditions often a mixture of these two degradation types occurs [29–35]. The key parameter affected
by the mentioned degradation is the threshold voltage
, in theory defined as the minimum gate-to-source
voltage needed to create a conducting path between source and drain (for normally-off devices). In other words
denotes the point where the device switches on. However, it should be noted that experimentally this transition is not abrupt but the drain current (
) rather increases exponentially with the gate voltage
(
). Experimentally
is typically estimated from the
-
curve or its derivative [28, 36].
Degradation evokes a shift, which is referred to as
. If the shift is so large that
no longer lies within the specified operating conditions,
this can cause failure at the circuit level.
is more pronounced at higher gate voltages and higher
transistor temperatures. The respective defect concentration responsible for
can be approximated using the charge-sheet
approximation [37, 38]. However, it was shown in [39] that this approximation underestimates the influence of single traps by a factor 2 to 3 in small devices. Taking this into account one can assume that a shift of 100 mV in a small device with
2 nm
oxide would be caused by a defect density on the order of
1011 to 1012/cm2 (
1018 to 1019/cm3). This corresponds
to
30-50 defects in a
100 nm
100 nm device. Note, though, that this
approximation is for defects sitting exactly at the interface of the oxide and channel region. In this work we will, however, deal with bulk defects in the oxide. The influence of each defect is then
dependent on its depth in the oxide, i.e. its distance from the interface. The above approximation is, however, a good approximation for the order of magnitude of the defect concentration sought after.
Furthermore, the variance (variability) increases in smaller devices, since single defects have a stronger impact with shrinking device geometries [3, 22–25, YWC1]. Hence, because of the aggressive downsizing of devices, resulting in much higher electric fields in the gate-oxide, BTI has risen to one of the most serious reliability concerns for modern CMOS technologies and has therefore increasingly attracted industrial as well as scientific attention. The main focus of interest for this thesis lies on the negative bias temperature instability (NBTI) of Si-based MOSFETs. This is due to NBTI in pMOS devices being much more pronounced than its positive counterpart (PBTI) in nMOS devices [28, 40, 41]. This, however, is only true for Si-based technology. For high-k materials, for example, PBTI can also play a crucial role [28, 42].
1.2 Measurement Techniques
In the following the two main measurement methods for BTI are presented: random telegraph noise (RTN) measurements and time-dependent defect spectroscopy (TDDS). To record RTN and TDDS data a special measurement equipment providing very high measurement resolution in time and current is required [36]. Their analysis allows one to identify the electric response of individual defects in the measured devices.
1.2.1 Random Telegraph Noise Measurements
Random telegraph noise/signal (RTN) is identified by discrete changes in the conductance of electronic devices generated by capture and emission of carriers at individual defect sites. A typical RTN signal (mapped to the gate voltage shift ) is depicted in Fig. 1.1. Analyzing such a signal can provide information on charge trapping dynamics of defects in the gate-oxide of a MOSFET. Unfortunately, this is feasible only for defects with rather similar capture and emission times [3],
which frequently change their charge state during a measurement. This criterion is quite limiting since there is only a small bias range at which the defects show similar capture and emission times,
which is different from defect to defect [3]. Furthermore, RTN analysis becomes difficult when dealing with defects which have more than just two states of different charge. Such defects showing
more complex behavior (see Section 1.3) might well be missed by the RTN analysis [3]. The defects that are most likely responsible for NBTI show such behavior [3, 18, 43], therefore different measurement
methods are needed to investigate their properties in more detail.
1.2.2 Time-Dependent Defect Spectroscopy
Figure 1.2: Left: Two typical recovery traces of a small-area pMOSFET from a TDDS
experiment from [YWJ1]. The measured data is depicted as the noisy black lines (top). The thick blue and red lines together with the symbols mark the emission times and step heights, unambiguous fingerprints of each defect which constitute the spectral map (bottom).
Right: Two TDDS spectral maps at two stress times,
=100 µs (top) and
=10 µs (bottom) from [YWJ1]. With increasing
stress time, the number of emission events in the map increases. The width of each cluster is given by the exponential distribution of the emission time constant
(considered on a log scale) and the extracted defects/clus-
ters are marked by +.
Time-dependent defect spectroscopy (TDDS) allows one to study charge trapping dynamics of individual defects in a systematic manner and to analyze defects with widely different charge capture and emission times [18, 44]. Since the measurement technique relies
on the identification and characterization of single defects, it requires the use of small-area devices (typically 100 nm100 nm and smaller) which usually contain less
than ten active defects in the gate oxide. Under these circumstances, the fluctuations originating from individual defects can be resolved in the measurements.
In TDDS experiments the device is stressed by application of a suitable stress-voltage for particular periods of time in order to make some of the defects in the device trap charge. This charge disturbs the device electrostatics, leading to a shift in threshold voltage,
. When the stress is removed, defects can emit their
charge again. Each such event leads to a discrete shift in the threshold voltage of a device which is measured during TDDS [3, 18, 44–46]. Two typical TDDS traces are shown in Fig. 1.2, where one can observe different
step heights. It is essential to understand that these observed step heights in TDDS do not depend on the microscopic structure of the defect but rather on the position of the charge within the oxide and its interaction with the channel [2, 47]. Therefore, provided that the
number of defects is small, a defect can be unambiguously identified by its step height.
On the other hand, the emission time at which the defect emits the captured charge again is determined by the atomic structure of the defect. Unfortunately, it is also a stochastic event [23, 24, 48–50], which is why a typical TDDS measurement consists of 100 or more traces as shown in Fig. 1.2 in order to obtain a sufficient number of emission events. The figure shows two different runs on the same device, where the discrete step heights occur at different emission times. The stochastic manner of the emission process can be seen since the emission takes place at different times for the two traces (in the second trace, for example, the emission of #4 even occurs before #3).
The step heights and emission times, , of each emission event, are collected and can be plotted
in a 2D histogram, as schematically depicted in Fig. 1.2 (left-bottom). Typical spectral maps for real measurements, in which many different traces are
recorded, are illustrated in Fig. 1.2 (right). The bright clusters are indicative of a single defect, and one can see a number of different defects with very different emission times within one device. For increasing stress times
more defects are able to capture a charge. This can be seen in Fig. 1.2 (right) where two spectral maps at the two stress times,
= 100 µs (top) and
= 10 ms (bottom) are shown. For the higher
stress time (bottom) the number of visible clusters has increased compared to the lower stress time (top).
Fig. 1.2 shows the case for negative-BTI (NBTI) in a pMOS device. Similar traces for nMOS devices and the positive-BTI (PBTI) effect can be seen in Refs. [51–53]. However, the focus of this thesis is on the NBTI effect in pMOS devices since (in Si-based technology) it is far more pronounced than its PBTI counterpart in nMOS devices [7, 26]. Nevertheless, the TDDS measurement method is also applicable for PBTI [51].
1.3 The Four-State Defect Model
Recently it has been demonstrated that defect behavior, as can be seen in Fig. 1.2, cannot be explained by a simple two-state model [YWC2, 54]. Rather, it was shown that the behavior can be explained when defects are
assumed to have a metastable state [3, 7] in addition to a stable equilibrium state in both charge states. Two of the states are electrically neutral ( and
) while two other states (
and
) are singly positively charged after hole trapping (see Fig. 1.3). In this model transitions involving charge exchange with the reservoir occur between
and
as well as
and
(see Section 2.2.1). The transitions between
and
as well as between
and
are assumed to be thermally activated transitions between two defect configurations in the same
charge state (see Section 2.2.4). Such a bi-stable defect model has rather complicated charge trapping dynamics, including two-step capture and emission processes.
The four-state model is described in greater detail in Section 3.1 where the involved transitions are modeled using the concept of potential energy surfaces (see Section 2.2) and the non-radiative multiphonon (NMP) theory (see Section 2.2.1). This four-state NMP model (see Section 3.1 and Fig. 3.2) has been very successfully used to fit a wide range of experimental data [3, 7, 46, 55, 56].
Figure 1.3: Schematic of the four-state model for NBTI defects as described in [56]. The states and
are electrically neutral while the states
and
are positively charged. Note that each charge state corresponds to an atomic configuration of the
responsible defect, in this case, the hydrogen bridge (see Section 4.2.2) in crystalline SiO
. Full lines correspond to a configuration change without charge
capture and emission, whereas dashed lines indicate a charge capture or emission event.
The four-state model has a set of parameters (see Section 3.1) which can be determined by the TDDS measurements. On the other hand, these parameters (except for two) can also be calculated for several
defect candidates using density functional theory (DFT). A comparison of the experimental and DFT-calculated parameters, therefore, can be used to judge whether a theoretical defect candidate is able to explain the measured TDDS data. This has been done for DFT
calculations in crystalline SiO in [56]. Unfortunately, the oxides in MOSFETs are not
crystalline but amorphous, contributing an additional level of complexity to this comparison.
1.3.1 Amorphous Oxide - Statistical Comparisons
TDDS experiments on the same device using different stress voltages, stress times and temperatures provide a wealth of information regarding the dynamics of electron/hole capture and emission by individual defects, which can be used for identifying the defects
involved. The largest complication for such an identification is related to the large variations (resulting in a broad distribution of parameters) seen in the measurements (see Fig. 1.2). These variations arise from the
amorphous nature of SiO in the gate oxide. Whereas in a crystalline structure the local
environment would be identical at each unit cell and therefore just a handful of distinguishable defects could exist, in an amorphous structure the conditions are different at each atom and therefore for each defect.
In order to judge whether a specific defect candidate is suitable to explain the experimentally observed behavior, DFT calculations were carried out using amorphous silicon dioxide (a-SiO) clusters as a host material. The structural disorder in
a-SiO
naturally also causes statistical variations in those
calculations. Therefore, a judgment whether or not a specific defect candidate is suitable to explain the behavior seen in measurements can only be made at a statistical level [YWJ1]. In Chapter 4 such a
statistical comparison is provided for the three most promising defect candidates: the oxygen vacancy/E
center, the hydrogen bridge, and the hydroxyl-E
center.
1.4 The Permanent Component of NBTI
Research indicates that NBTI consists of two components dominantly contributing to the device degradation [57–60]. In measurements as described above, after stress, the signal often does not recover fully to the initial “unstressed” level. One, therefore, distinguishes between the recoverable component (RC) and a more or less permanent component (PC). However, it has been shown that even the PC can be annealed at higher temperatures [59, 61–65], which implies that the PC is also recoverable, though at considerably larger time-scales than the RC. This makes it rather difficult to give a proper definition of how to accurately define the PC.
Furthermore, it is not possible to measure the two components separately and the RC normally overshadows the PC. The extraction of the PC is thus very challenging. The most straightforward approach would be to wait until the recovery of has leveled out. Due to the very large timescales
involved (even for short stress times), this is, however, extremely impractical. Therefore, the current understanding of the PC is somewhat vague. To explain the permanent component of NBTI a
hydrogen release model was suggested recently [YWC1, YWC3] (see Section 3.2).
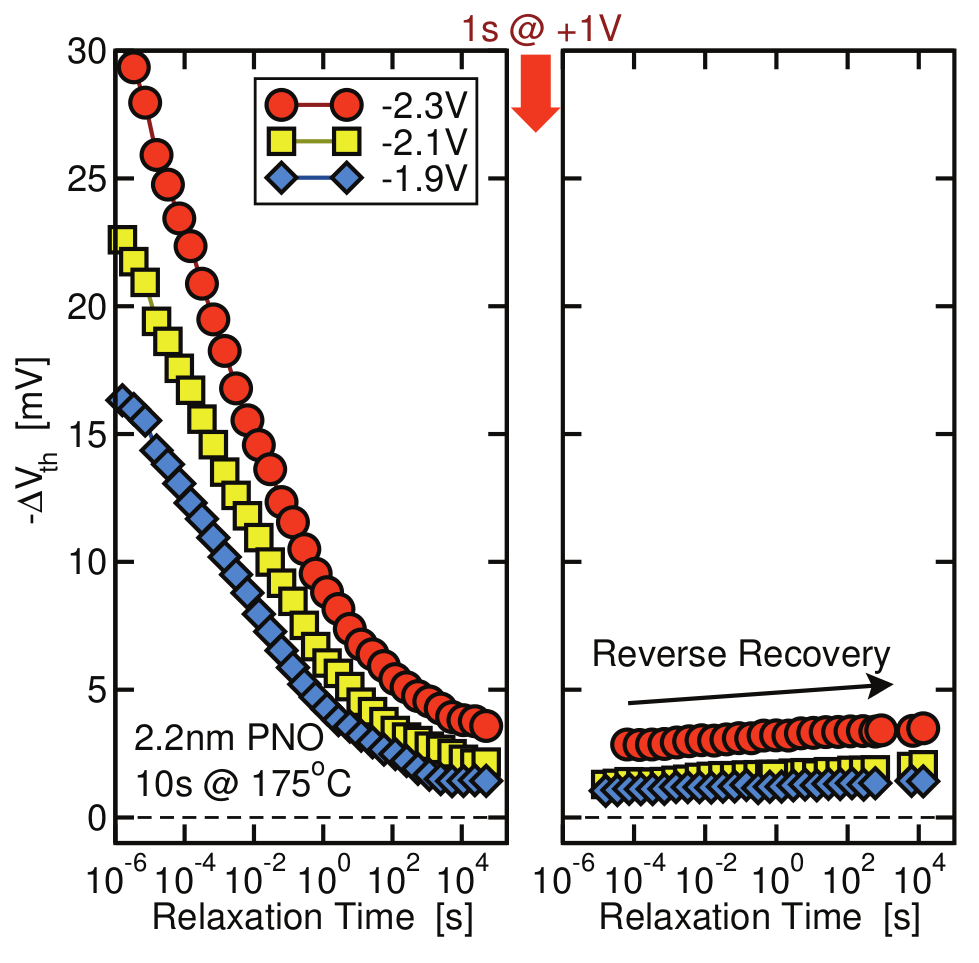
Figure 1.4: Plateaus in NBTI recovery data from [60] indicating the existence of a permanent component. A short positive pulse is expected to remove the recoverable fraction of degradation (between the left and right panel), whatever remains is considered the permanent component. Note that in the right panel there is considerable amount of reverse recovery (see [60] for further details).
1.5 Effects not Covered by the Four-State Model
As described in Section 1.3, the four-state model for NBTI covers very successfully many experimentally observed defect features. However, there is experimentally observed defect behavior which this model is not able to describe without additional assumptions, like for example the previously introduced permanent component of NBTI. In this thesis, three such effects will be investigated in more detail:
1.5.1 Volatility
One additional feature that is observed during RTN and TDDS measurements is volatility [44, 66, 67]. Defects have been found to frequently disappear and reappear in the measurements (see Fig. 1.5), and can sometimes even disappear completely from our observation window [44, 67, YWC4]. This has been proven to occur for a considerable fraction of the defects and can therefore not be regarded as a rare event [YWJ1]. Hence, a consistent model of oxide defects must be able to not only describe their behavior when electrically active but also allow them to disappear and reappear during measurement cycles. An attempt to extend the current model to include volatility effects is made in Chapter 5.
1.5.2 Double Capture/Emission Events
In measurements, defects that are able to capture or emit twice within one TDDS-trace [68] are encountered. Even though it is often speculated that this is due to two defects interfering with each other, it might as well be one defect having three possible charge states. However, the sole existence of three stable charge states is not enough to explain experimental data as seen in Fig. 1.6. Their energetic positions and barriers to switch between each other also have to be considered. In Chapter 7 this is investigated in more detail and several defect candidates are examined on their suitability to explain double capture or emission events using the above assumption. To our knowledge, no such effect in RTN measurements has been published up to now. However, it will be shown in Chapter 7 that due to the limitations of RTN analysis the occurrence of a double emitting or capturing defect in RTN analysis is expected to be very unlikely.
1.5.3 The Permanent Component
When modeling NBTI by a four-state model and a supplementary double-well model it was shown that it is in principle possible to reproduce the characteristics of the measurement data [69] (see Fig. 1.7). Here the recovery after NBTI stress is compared to the results fitted using such a model. Even though the model is capable of fitting the experimental behavior, it is not entirely satisfying. Since it does not involve fundamental physical parameters, the calibration is not universal across technologies. Therefore, the model is neither able to give insight into the underlying physical process nor to predict degradation.
Recent long-term degradation and relaxation experiments have initiated the development of a gate-side hydrogen release model [YWC1, YWC3, 70]. This model assumes that hydrogen is released from the gate side of the oxide to migrate towards the channel. This model is not only able to cover the permanent component of NBTI, but also capable of explaining several experimental observations like hydrogen release during NBTI stress (see Section 3.2).
1.6 Scope of This Work
The focus of this thesis is to widen the understanding of possible defect behavior when considering amorphous (a-
) as a host material, as is the case for the oxides of a
typical Si-based MOSFET. As already mentioned above, this means that for every discussed aspect a large number of different DFT calculations had to be carried out in order to obtain statistically reliable data to compare with experiment.
The statistical comparison of defect parameters in order to narrow down the number of possible defect candidates responsible for the NBTI effect is one of the main scopes of this work (see Chapter 4), showing that hydrogen (H) is very likely to play a key role. However, as already mentioned, the NMP four-state model is not able to explain experimentally observed behavior such as volatility and double capture/emission. In Chapter 5 a possible mechanism responsible for this effect is discussed and the NMP four-state model is extended accordingly.
Since the importance of H is highlighted in these two chapters, Chapter 6 then explores the possible dynamics for H within the amorphous oxide in more detail. It is of special interest to investigate the energy barriers that have to be overcome by the
H atoms when moving through a- to draw conclusions for the recently suggested H release model for the permanent component of NBTI. Although it may seem that the two models describing the recoverable and permanent component of NBTI are very different, it will be shown that they
could have a common underlying cause and are therefore closely connected, as previously suggested in [58].
Finally, Chapter 7 takes a closer look at the assumption of parabolic potential energy surfaces (see Section 2.2) and the possible impact on the capture and emission times predicted in the NMP four-state model. This investigation also takes negatively charged defect states into consideration, thereby discussing possible explanations for the observed double capture and emission processes.
2 Theoretical Background
This chapter presents the underlying mathematical concepts of the calculations in this thesis. These are, above all, the density functional theory (DFT), the potential energy surface (PES) and the non-radiative multiphonon (NMP) theory. These concepts are the mathematical basis to formulate the NBTI models in the following Chapter 3.
2.1 Density Functional Theory
DFT has become a standard approach in many fields of solid-state physics because of its applicability for a broad range of problems. It is based on the theorems by Hohenberg and Kohn [71, 72]:
-
• For any system of interacting particles in an external potential
, the density is uniquely determined. In other words, the external potential is a unique functional of the density.
-
• A universal functional for the energy
can be defined in terms of the charge density. The exact ground state is the global minimum value of this functional.
The energy of the system can be written as
The classical energy of a charge distribution is given by
,
with the kinetic energy term
, the potential energy term due to positive nuclei
, and the so-called Hartree term
describing electron-electron interaction.
The term is referred to as the exchange-correlation energy containing all complicated
many-body effects that are not accounted for in the other terms. It is usually treated as a separate exchange (
) and correlation (
) part [73].
It should be pointed out that is the only of the energy functionals which cannot be calculated analytically and
therefore has to be approximated. Depending on the problem and the desired accuracy multiple
and
have been formulated, as for example the local density approximation (LDA) [72], the generalized gradient approximation (GGA) [74, 75], or the Perdew–Burke–Ernzerhof (PBE) functional [76], but also so-called hybrid functionals, which will be discussed in Section 2.1.4.
The second Hohenberg-Kohn theorem states that by minimizing eq. (2.1), the ground-state density and energy can be obtained.
The kinetic energy cannot be calculated directly from the density in pure DFT, but only when mapped to single-particle orbitals. Kohn and Sham, therefore, proposed to use a fictitious system of noninteracting electrons that is constructed in such a way that its density is the same as that of the interacting electrons [72]. Even though the wave functions in Kohn-Sham DFT do not have a physical meaning, it is common to draw conclusions from the Kohn-Sham eigenlevels, e.g. when calculating band structures [77] or defect levels [78]. The exact wave function of the independent electrons is simply the product of the spin-orbital for each electron. This can be written as a slater determinant:
This formulation obeys antisymmetry by construction and also respects the indistinguishability of the electrons (therefore the Pauli principle for electrons follows naturally), where the are single-particle orbitals. Summing the
probability density (
) of the wave functions over all of our
orbitals gives the electron density:
Now the true ground-state density of the system is reproduced from the KS system by choosing a suitable external potential . Thus, the Schrödinger equation in the
Kohn-Sham formulation is
with being the eigenvalue of the Kohn-Sham
orbital. This equation can be solved self-consistently by calculating
for an initial guess of the density, solving
the eigenvalue eq. (2.6) to obtain a new density, which is used again for a new guess of
. This loop iterates until the desired accuracy
is reached. The resulting energy of the ground state is hence given by:
However, the solution is only as accurate as the chosen functional allows. On the other hand, more accurate functionals make the DFT
calculation computationally much more expensive. Therefore, a compromise between accuracy and computational time always has to be sought. In this work the vast majority of the calculations were performed using computationally very expensive hybrid-functionals (see Section 2.1.4). This was necessary because these functionals are much more accurate compared to
non-hybrid-functionals, when calculating the electronic structure, as well as the total energies [77, 79, 80].
2.1.1 Simulation Software: Why CP2K?
Some twenty years ago the results of DFT calculations could still vary widely when using different software packages, each with different approaches to the problem. As could be shown recently in a major benchmark study [80] covering 40 DFT methods, the deviations between the different software packages have been reduced to a level where nearly all codes produce comparable results. When dealing with amorphous structures, as in this thesis, results can only be compared at a statistical level, since every amorphous structure differs from another. In order to obtain reliable statistics a large number of calculations on different structures has to be carried out. Therefore, a code requiring relatively low computational resources for our purposes was sought. It was found in the CP2K software [81] (an open source Γ-point only code1), which meets these requirements well.
The popular DFT codes suitable for these calculations all use either Gaussian basis sets (Gaussian [83], PSI [84]) or a plane-wave basis set (VASP [85], Wien2k [86], Quantum ESPRESSO [87]), each having its advantages and disadvantages (see Section 2.1.3). The approach of the CP2k software is the so-called Gaussian plane wave (GPW) method. In this method, the system is represented in both bases in order to use the less time consuming one for the calculation while maintaining accuracy. Furthermore, for reducing the computational costs when calculating Hartree-Fock exchange integrals, an auxiliary density matrix method (see Section 2.1.5) is available.
1 k-point sampling is available since version 3.0 as a post-processing step [82].
2.1.2 Basis Sets
In order to solve the Kohn-Sham equations (see eq. (2.1)), the wave functions are expanded into a chosen basis set of functions
Two popular choices are Gaussian and plane wave functions, each having its advantages and disadvantages.
Plane Wave Basis Sets
Plane waves are a natural choice of basis set when describing periodic systems. Furthermore, they are independent of the particle position and, in principle, form a complete orthogonal basis [88]. The density represented in this basis set is:
where is the volume of the cell,
is the reciprocal lattice vectors and
is the expansion coefficients. The density
is the Fourier-transformed density
on a real-space grid.
Fast Fourier transform techniques allow for a faster calculation of the Hartree energy and checking the convergence of a calculation using a plane wave basis set in a straightforward matter. However, for properly describing the density in a plane wave basis, a larger number of basis set elements is required relative to a Gaussian basis set. Also, since the inner wave functions vary too rapidly, the use of pseudopotentials is inevitable.
Gaussian Basis Sets
Gaussian basis sets, on the other hand, are known to already deliver good results for small basis set sizes. In a Gaussian basis set the density is written as:
where is the number of electrons, and the
are the molecular orbitals. They are
atomically centered functions which allow for a compact description of the wave function and also for all-electron calculations. Furthermore, efficient algorithms exist to analytically calculate matrix integrals. On the other hand, a Gaussian basis is non-orthogonal, and the
incomplete basis set can lead to superposition errors, linear dependencies, or over-completeness. Further disadvantages are their dependence on the atomic positions and possible wrong asymptotic behavior as well as their not implicit periodicity, especially when using
periodic boundary conditions.
2.1.3 The Gaussian Plane Wave Method
The Gaussian plane wave (GPW) method is a hybrid method using both Gaussian and plane wave basis sets [88, 89] implemented in the Quickstep [90] module in the CP2K code [81, 82]. In a given system of atoms the electrons can be divided into core electrons
(close to the nucleus) and valence electrons (further from the nucleus). In this method, in order to integrate out the core electrons, pseudopotentials are used [91]. The valence electrons wave functions are described in a Gaussian basis set while the density is represented in
a plane wave auxiliary basis. Replacing the core electrons with a pseudopotential provides a smoothly varying density, which can be easily mapped from the Gaussian basis set to a plane wave basis set. Furthermore, fewer Gaussian functions are required to produce the
characteristic cusp behavior near the nucleus. This allows for easier mapping of the density from a Gaussian to a plane wave basis set. The first representation of the electron density is based on an expansion in atom centered,
contracted Gaussian functions
with the density matrix and the wave functions
constructed by primitive Gaussian functions. The intermediate basis for the density used in this approach is a plane wave basis:
in which is the volume of the periodic cell in real space.
The different parts for constructing the analytical form of the energy functional in the GPW Method yield [88]:
with the kinetic energy , the terms originating from the local
and non-local
pseudopotentials (
and
respectively), the Hartree energy
as well as the exchange correlation energy
and the interaction energies of the ionic cores with charges
and positions
, denoted by
. The final energy functional is then [90]:
The kinetic and potential energy are computed analytically using a Gaussian basis set, then the density is mapped onto the plane wave basis to calculate . This significantly reduces the calculation cost since the favorable basis set can be
used for each part where it is computationally less expensive. Consequently, it allows to study larger systems with the same amount of computational resources than would be possible using either of the two basis sets alone.
2.1.4 Hybrid-Functionals
In Kohn and Sham’s approach, the key approximation is the exchange-correlation functional (). An
appropriate choice of
is essential for accurate calculations of material properties. Well known
approximations are, for example, the LDA [72], GGA [74, 75] and PBE [76] functionals [92]. The local density approximation
(LDA) functional was the first one to be introduced, and only depends on the electronic density at each point in space. It has been surprisingly successful but is also known to overestimate the binding
energies. An improvement was achieved by the generalized gradient approximation (GGA). In this approximation, the exchange-correlation energy not only depends on the local electron density but
also on its gradient. Currently, a very frequently used functional is the Perdew-Burke-Ernzerhof (PBE) functional, a simplified GGA in which all parameters are fundamental constants. Especially for
our purpose of calculating defect energies in
there are two known limitations to these potentials:
-
• They are known to not accurately reproduce the band-gap (LDA and GGA underestimating it by up to 40%) [93].
-
• They are known to not satisfactorily describe localized defect states [94, 95].
Both are essential for understanding defect behavior in SiO. Therefore, for the vast majority of the calculations in this
thesis so-called hybrid functionals are used. They typically use a portion of Hartree-Fock (HF) exchange which is explicitly calculated for all electrons in the system. The band-gaps and localized defect states calculated using these hybrid functionals show significant
improvement compared to the local and gradient-corrected approximations. The most known example of a hybrid functional surely is the Heyd-Scuseria-Ernzerhof (HSE) functional [96]. For the calculations in this work, the chosen functional was the PBE0 TC LRC
hybrid functionals [97] with the parameter
of HF exchange energy:
The parameter was set to a value of 0.2 since results were promising when using this value [79, 97]. In a
Γ-point only approximation, as used in CP2K (see Section 2.1.1),
can be computed as:
With being the density matrix
and
the exchange
integrals
where are the single-particle orbitals and
is a truncated coulomb operator
defined by a cutoff radius
[97]:
2.1.5 The Auxiliary Density Matrix Method
Computing the HF-exchange, energy scales with the fourth power of the number of used basis functions [98]. By introducing an auxiliary density matrix , the calculation can be accelerated significantly.
thereby needs to be smaller (or faster decaying) than
. In the auxiliary basis set the wave functions are described as:
where is the Gaussian orbital coefficient. The
density matrix is constructed using these coefficients as:
The coefficients can be obtained by minimizing the square difference for the occupied wave functions in the full and auxiliary basis set:
The energy then can be computed as:
where is the HF exchange energy,
whereas
is the exchange energy when
using the GGA functionals. The assumption made is that the difference in the exchange energy for different basis sets
and
is approximately the same when using HF and GGA functional [98]. This approximation is
able to considerably reduce the computational costs of the calculation when using hybrid functionals.
2.2 The Potential Energy Surface
Vibrational states are usually associated with stretching or bending modes in molecules or phonons in a solid. The interaction of the electrons and nuclei is described in the full Schrödiger equation of the system. This equation, however, is not analytically solvable for all systems except the simplest molecules. The standard approach to simplify the problem was first suggested by Born and Oppenheimer in 1927 [99]. The approximation uses the fact that the mass of the nuclei is orders of magnitude higher than the electron mass, which allows one to separate the equation into an electron and a nuclei part. The problem then reduces to the only-electron equation for fixed nuclei positions [99], in the zeroth order approximation. In the following the very closely related Huang-Born approximation [100, 101] will be considered:
Here the problem is also split into an equation for the electrons (degrees of freedom , wave function
) and one for the nuclei (degrees
of freedom
, wave function
). These equations contain
Coulomb contributions from the electron-electron (
), electron-nucleus (
), and nucleus-nucleus (
) interactions as well as the kinetic
energies of the electrons (
) and the nuclei (
). The solution
is usually referred to as the adiabatic potential
energy or also adiabatic potential energy surface (PES). It is the solution of the electronic part eq. (2.23) and acts as a potential for the nuclei in eq.
(2.24).
The PES describes the energy of a given system of atoms, in terms of the degrees of freedom of the system and is thus a multidimensional object of dimension
. Therefore, a fully
quantum mechanical treatment is impossible. Even a quantum Monte-Carlo-like treatment is unfeasible since the required computational resources to calculate the PES would be very high. It is thus
necessary to approximate the quantum mechanical nuclear problem as a classical one or to approximate the potential energy surface. For our purpose of calculating charge transfer reactions, for practical
reasons, the atomic degrees of freedom are also reduced to just one coordinate, the configuration coordinate (CC), describing the motion of atoms. Most approximations assume a parabolic shape of the PES for small deviations from the minimum-energy position
(see Chapter 7), which allows one to approximate the PES as a harmonic oscillator potential. It should, however, be noted that there have also been attempts of other approximations [102, YWC6].
2.2.1 Non-Radiative Multiphonon Theory
Figure 2.1: The configuration coordinate diagram featuring the PESs ( and
) involved in an example charge transition. The PESs’ min-
ima are located at their equilibrium configurations
and
respectively. Radiative transitions involving only photons
(blue) occur without a change in the CC. Non-radiative transitions (green), on the contrary, involve a change in the CC, thereby being able to overcome the barrier defined by the intersection point of
and
. Hence, the barrier for the non-radiative transition is per
definition always lower than (or at maximum equal to) the radiative transition.
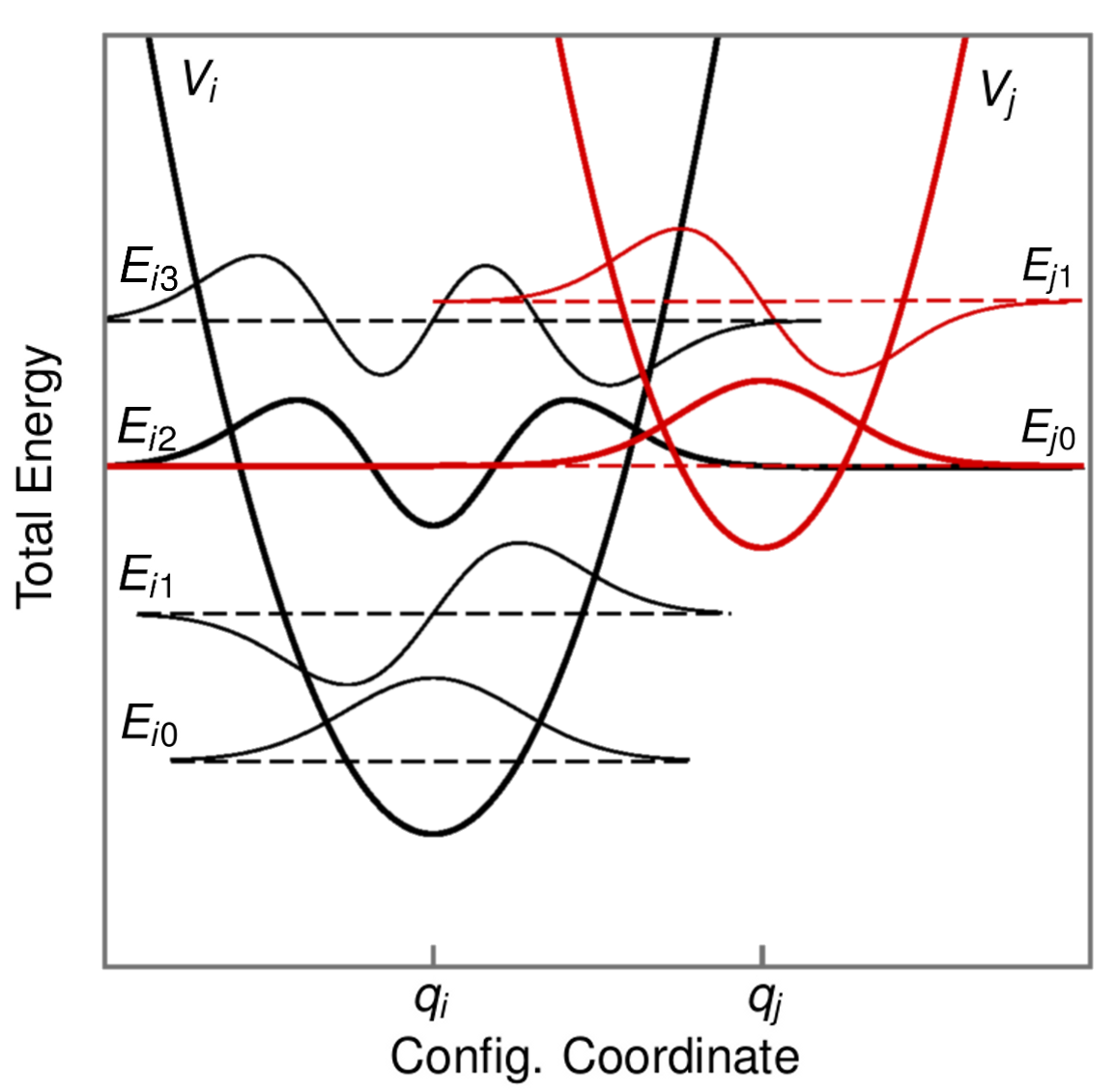
The systems treated in this work can all be assumed to stay in a thermal quasi-equilibrium most of the time, interrupted by transitional motions of very short duration for charge state changes. These transitions, therefore, are sufficiently described as occurring
instantaneously [103]. In the configuration coordinate diagram (see Fig. 2.1) a charge transfer process is the transition or vice versa. In Fig. 2.2 the wave functions for the corresponding eigenenergies are depicted schematically. In the quantum mechanical picture, the transition rate depends on the overlap of these wave functions. Note that transitions
between different PESs can occur either through radiative or non-radiative transitions (see Fig. 2.1). The radiative transitions occur at a fixed CC and therefore do not need structural change (phonons) to
occur. Non-radiative transitions can only occur phonon-aided and therefore favorably near the crossing of PESs. The transitions, therefore, are referred to as non-radiative multiphonon (NMP) transitions [104, 105]. Note that the energy barrier for the non-radiative transition in Fig. 2.1 is considerably lower than for the
radiative transitions.
The Line Shape Function
Figure 2.2: Charge transfer reaction for two PESs in the quantum mechanical picture as shown in [101]. Each of the two PESs corresponds to one charge state of the defect where the left one () represents the initial and the right one (
) the final charge state. Their corresponding wave functions
and eigenenergies are depicted as solid and dashed lines, respectively. An NMP transition only occurs when the initial and the final energies coincide as it is the case for
and
. Then the overlap of their corresponding vibrational wave
functions enters the calculation of the line shape function eq. (2.32) and consequently determines the NMP transition probability [101].
In optical spectroscopy line shape functions describe the thermal broadening of absorption peaks [104–106], but the concept is also applicable to non-radiative carrier capture at defects in semiconductors.
Using first order perturbation theory and the Franck-Condon principle [104, 107–109] the rates for NMP transitions described above can be calculated using Fermi’s golden rule [110]:
with the perturbation operator . Here,
and
denote the initial and final state of the transition, where
and
are electronic and
and
are vibrational states, similar as in Fig. 2.2. The Frank-Condon approximation states that it is possible to rewrite the matrix element
in the following way:
separating into an electronic and nuclei part.
Using this transformation we now define
and can then rewrite eq. (2.25) for the transition rate as
where is referred to as the Franck-Condon
factor, determined by the overlap of the nuclei wave functions.
is called the electronic matrix element describing the
electronic interactions, for example the electron transition between the two states in Fig. 2.2. Both
and
are the probabilities for the respective reaction to
occur. Typically
making
the decisive probability for the
transition rate. In the NMP theory,
has to comprise all thermal excitations.
Therefore,
must be averaged over all initial states
. Furthermore, all reachable final states have to be summed over:
The largest contribution to the so-called line shape function (LSF) comes from those energy levels which lie close to the intersection of the two PESs (see Fig. 2.2). Thus, it is obvious that the line shape
function and the rates are strongly dependent
on the shape of the PESs. This shape is very complex and will be discussed in Chapter 7. Using the LSF eq. (2.30) simplifies to:
In the classical limit the LSF falls down to a Dirac peak at the intersection point, i.e. the transition then is only governed by the position of the intersection point. For calculating the LSF the quantum mechanical solution for the PES has to be known. Analytically, however, this is only possible for a few simple cases. If the PES has a more generic shape the quantum mechanical treatment becomes very unpractical at the very least. In Chapter 7, therefore, only the classical limit is applied.
NMP Transitions with a Whole Band of States
Figure 2.3: Configuration coordinate diagram in the hole-picture for an example charge transition (hole capture), showing not only the top, but
also the next few states of the conduction and valence band. The energy of the transferred charge carrier is now not uniquely defined for the initial state since the hole is initially in one of the valence band states. For this reason, one has to introduce a summation over all
possible valence band states in eq. (2.33). For the back transition
(hole emission) the final
state is not exactly defined, necessitating the summation over all conduction band states in eq. (2.33).
Up to now, we have looked at NMP transitions involving just two states. In the scope of this work dealing with oxide defects in MOSFET devices, there is, however, a whole band of states to interact with, namely the conduction and valence bands. Since the
conduction and the valence bands both form a continuous spectrum, the electron concentration and hole concentration
depend on the density of states
for the conduction band and
for the valence band and the carrier distribution
functions for electrons
and for holes
[103]:
In the following we will consider the transition as depicted in Fig. 2.3. This marks the transition from a neutral to a positive charged state by either electron emission into the substrate conduction band or hole capture from the valence band2. Here,
denotes the electrostatic trap level describing
the position of the neutral state
with respect to the conduction band edge
or valence band edge
in the absence of an electric field [101] (see also Section 4.3.2). A full set of transitions rates can be formulated using eq. (2.33) and (2.32) [101]:
The above rates describe the situation for a hole-trap as it will be called throughout this thesis. These rates can be adapted for the case of an electron-trap switching between a neutral and negative charge state.
2 Note that a hole being captured from the valence band and an electron being emitted into the conduction band are equivalent. Of course the same holds true for an electron being captured from the conduction band and a hole being emitted into the valence band. These different points of view are referred to as the “electron-picture” and the “hole-picture”.
2.2.2 Interaction of a PES with an Electric Field
Figure 2.4: In a simple (first-order) model the potential depends linearly on the applied field and the distance from the oxide accordingly. Here the neutral PES remains unaffected whereas the PES for the charged
state
is shifted according to eq. (2.35).
Note that the change in the reaction barrier
does not depend linearly on this shift
since
is only dependent on the intersection
point of the two PESs. In this figure the shifts
and
are chosen equally large, but resulting in different
and
.
The presence of an electric field imposes an additional potential in eq. (2.23) and (2.24) thereby shifting the PES along the energy axis. Throughout this thesis it will be assumed that this does not affect its shape. For oxide
defects in MOSFET devices this, of course, is highly relevant, since there is a constant change of the field in the oxide while operating. In a simple (first-order) model there is a linear relation between the potential, the applied field and the distance from the oxide. At a
certain depth in the oxide the potential energy shift
due to the presence of the electric field
yields [103]:
where denotes the charge. Using this approximation the PES in
Fig. 2.4 shifts relatively to each other when an electric field is applied, thereby changing the barriers which are to be overcome and henceforth
also the rates in eq. (2.34).
2.2.3 Strong and Weak Electron-Phonon Coupling
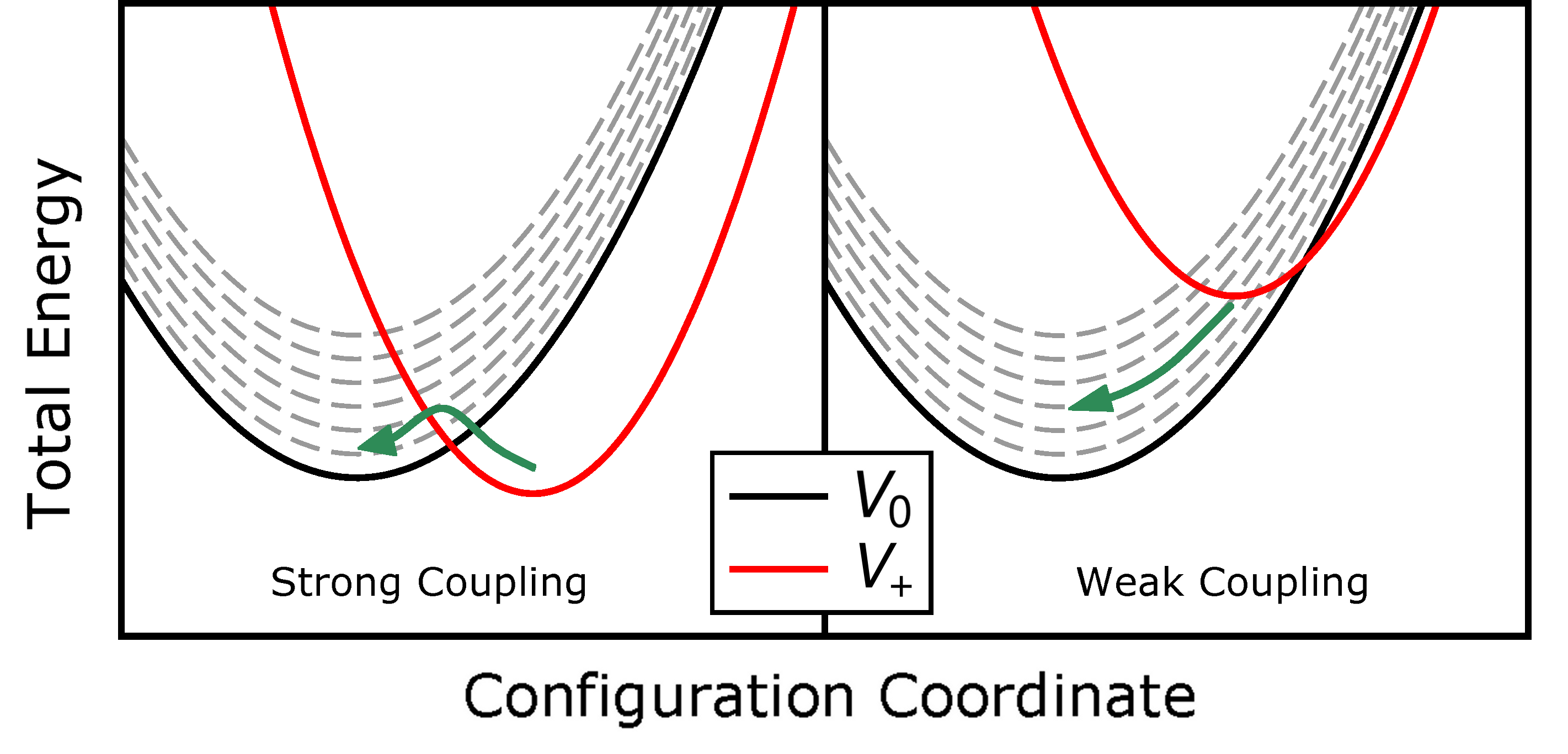
Strong and weak electron-phonon coupling in the literature [101, 111] is mostly associated with the parabolic approximation of the PES. However, within the scope of this work, an explanation as in [112] and Fig. 2.5 is chosen to make this approach also applicable for non-parabolic PESs.
Figure 2.5: Configuration coordinate diagram for an example case of hole emission. Similar to Fig. 2.3 all valence band states (grey) are incorporated. In the right panel, the intersection point lies outside the two energy minima. In this case, one valence band state can always be found which intersects the positive PES at, or very close, to its minimum. Therefore, this transition is basically barrier-free. This case is referred to as weak electron-phonon coupling (WC). By contrast, in the left panel, the intersection point of the two parabolas is located between their two energy minima. This is the strong electron-phonon coupling case (SC) where the consideration of all valence band states does not influence the reaction barrier.
In the classical limit, transitions between two states take place at the intersection of two corresponding PESs. We assume that this intersection point determines the reaction barrier that has to be overcome. However, this only holds true for the case of strong electron-phonon coupling (SC) as depicted in Fig. 2.5 (left). The right side of this figure shows an example of a transition in weak electron-phonon coupling (WC). Here the crossing point of the PESs lies on the opposite side, seen from the positive PES’s minimum. Hence, one can always find an excited state of the neutral PES which intersects the positive PES at, or very close to its minimum. The transition into this excited state is, therefore, nearly barrier-free, as is the following relaxation into the ground state of the neutral PES.
It should be noted that in this model, particularly in the WC regime, the exact shape of the PESs does not influence the result. It does, however, define the limits when a transition is in the SC or WC
regime. When in the SC regime, the shape of the PESs also defines the location of the intersection point and, therefore, the transition barrier. The interaction with an electric field (eq. (2.35)) can cause the PESs to shift relative to each other, thereby possibly changing the coupling regime The NBTI defects observed in our measurements are
usually in the strong coupling regime, in which a forward and backward reaction barrier is encountered. Defects which do not show this coupling regime “naturally” (i.e. at a shift ) are thus very improbable candidates to explain the
NBTI behavior.
2.2.4 Pure Thermal Transitions
Figure 2.6: Schematic of a pure thermal transition along one PES between two states with CC and
. The barrier to overcome for a transition is
or
respectively. These barriers en-
ter the rate eq. (2.36).
The PES of a system of atoms does not only have one minimum. Depending on the atomic configuration several local minima (states) can be found on one PES [113]. These states are separated by an energy barrier (see Fig. 2.6) that can be overcome by pure thermal excitation and are described by transition state theory [114, 115]. The rate to overcome such a barrier is
with being the attempt frequency and
the barrier that has to be overcome for the reaction from a state
to a state
(if tunneling is neglected). This type of equation is know as
the Arrhenius law [116, 117].
Even though the treatment of this type of transitions seems much easier than the charge capture/emission transitions described above, the determination of the so-called minimum energy-path (MEP) is not. The MEP is defined as the interlinking path with the lowest
(i.e. the lowest pass summit) to cross
between the two states. A method for its calculation will be discussed the following section.
2.2.5 The Nudged Elastic Band Method
A very popular method to determine a minimum energy path on a PES connecting two states of the same charge, as described above, is the nudged elastic band (NEB) method [118, 119]. In the NEB method, several atomic configurations along the reaction path (referred to as images) are virtually connected via spring potentials. This system is then optimized with respect to the total energy (the image energy plus the spring potential for each image). It should be noted that even though the NEB is a very powerful tool, it is only capable of finding local minimum energy paths. It is entirely dependent on the chosen images and does not find the global minimum energy path. Therefore, the choice of suitable starting images is very important for all the different species of NEB calculation methods.
The simplest of such chain-of-states methods is the plain elastic band (PlEB) method [118]. In this approach the force acting on a certain image
consists of the force due to the system not being in its potential energy minimum
and the force imposed by the virtual
springs
:
, thereby, interlinks the images and
consequently depends on the neighboring images
and
and the spring constants
of the springs:
Using this definition, an objective function can be defined as:
This function is then minimized with respect to the atomic coordinates of the images while keeping the end points fixed and yielding images along the minimum energy path of the reaction sought
after. The PlEB, however, suffers from some shortcomings that do not guarantee the PlEB finding the proper minimum path. First, it is known to cut corners and therefore miss saddle point regions. Secondly, images tend to slide down the PES reducing the
resolution in the saddle point region, which is the actual region of interest [118, 120].
Figure 2.7: Explanation of the NEB method from [121]. Two components make up the nudged elastic band force eq. (2.40): the spring force
, along the tangent
, and the perpendicular force due to the po-
tential
. The unprojected force due to the potential
is also shown for completeness. The minimization of these
forces leads the NEB-path to converge to the minimum energy path (MEP).
Johnson et al. [118] therefore proposed to refine the PlEB in order to fix these shortcomings. In this refined
method, the force on each image along the pathway is split into the component parallel and perpendicular to the direction of the band .
can be minimized directly, without having to define an objective function as for the
PlEB above. If converged, the result of the NEB method is equally spaced images along a trustable minimum energy path (see Fig. 2.7). However, this also demonstrates the main shortcoming still being inherent to the NEB
method: Since the images are equally spaced, in general also this method will miss the exact barrier
of the path, if one of the points does not coincidentally lie on the exact saddle point.
The NEB, therefore, gives too low energies
.
Climbing-Image NEB
The above problem has led to the development of the climbing image NEB (CI-NEB) method by Henkelmann et al. [122]. The CI-NEB is just a small but effective modification to the
NEB method. In the CI-NEB the NEB-force for the image having the highest energy is replaced by
which is the full force due to the potential with the component along the NEB-path inverted. Furthermore, there are no spring forces applied to the image . This modification causes
to climb along the NEB-path to the first
order saddle point, providing a more accurate estimation of
than the NEB method. Therefore, it is the preferred method for all calculations for
determining the thermal transition barriers throughout this thesis. For the scope of this thesis the force constant for the connecting springs was set to 2 eV/Å2, since this has been shown to produce good results [YWJ1, 79].
3 NBTI Models
In this chapter, the two models which will be used as a basis for the calculations and considerations in the subsequent chapters are introduced. The knowledge of these models is required to follow the results and considerations in this work. The models will be outlined to show the basic concepts, whereas the underlying mathematical formulation was already given in the previous Chapter 2.
As the NBTI effect has been known since the 1960s [123, 124], many different models have been proposed to explain the results of charge capture and emission measurements. In the past years, it has become clear that NBTI consists of two dominant components which contribute to the device degradation [57–60]. One distinguishes between the recoverable component (RC) and a more or less permanent component (PC). However, it has been shown that the PC can also be annealed at higher temperatures [59, 61–65]. This implies that the PC is actually recoverable too, though at considerably larger time-scales than the RC, which makes it rather difficult to give a proper definition of the PC. Furthermore, it is not possible to measure the two components separately since the RC normally overshadows the PC.
Experimental results and theoretical calculations have led to the development of the NMP four-state model to explain the recoverable part and a hydrogen (H) release model explaining the PC, both of which will be discussed in this chapter. Even though the models seem to be very different at first glance, it will be shown in the following chapters that they very likely originate from a common cause and are therefore suspected to be connected.
3.1 The NMP Four-State Model for NBTI
Over the years many different models have been proposed to explain NBTI. The early models relied on elastic carrier tunneling between the substrate and oxide defects [37, 125–128]. However, these models were not able to capture the temperature and bias dependence observed in experiments. Other models are based on the well known Shockley-Read-Hall (SRH) model [129] modified to account for the tunneling effect [130] and the thermal activation seen in RTN data [2, 131]. The best-known example is the model suggested by Kirton and Uren [2] which is still very widely used. In this work, the authors account for structural deformation during the charge capture and emission process by introducing non-radiative multiphonon processes (see Section 2.2.1) in this context for the first time. In this model, a Boltzmann factor is introduced in the SRH rates to account for structural relaxation [2]. While this also accounts for the temperature dependence, it still neglects the strong bias dependence of these Boltzmann factors [3, YWJ1]. In the following, the experimental results and theoretical considerations that lead to the NMP four-state model will be discussed. This model forms the basis for the calculations throughout this thesis.
3.1.1 Experimental Evidence for a Four-State Model
As already described in Section 1.2, TDDS and RTN measurements allow for characterization of single defects in MOSFETs. The use of spectral maps (see Fig. 1.2 (left)) allows us to study the voltage and temperature dependence of the capture () and emission times (
) of these defects. From those measurements, plots like
Fig. 3.1 can be extracted. Typically in such plots, the points with similar capture and emission constants are obtained from RTN analysis, whereas for the other points TDDS is used. The main findings of the
last years, based on these extractions, can be summarized as follows [132]:
Figure 3.1: TDDS data of a fixed positive charge trap (left) and a switching trap (right) from [38] for 125 °C and
175 °C [18]. The characteristic feature of a switching trap is the drop in emission time
constants at the relaxation voltage (right). This feature does not appear for fixed positive charge traps. Their emission time constant is nearly bias independent within the range around and above the relaxation voltage (left).
-
•
is exponentially dependent on the voltage. Mathematically this can be described by the relation:
[3], where
is the oxide field and
,
and
are constants.
-
• Both
and
, are temperature activated processes. In Fig. 3.1, therefore, the curves for the higher temperature have lower
and
.
-
• On the basis of the emission behavior, two types of traps can be distinguished:
Both these observations can be explained assuming a four-state model with metastable states, as was shown in [3, 132, 133]. Whereas for the fixed positive charge traps one of the four states1
is inaccessible during measurement conditions (i.e. an effective three-state model, one of them metastable), one has to include a second metastable state for the switching traps. This results in a four-state NMP model which will be formulated in the context of
PESs later. It should be noted that a Si- band structure model, described in Appendix A.4, is assumed for the charge capture and emission processes. In this model, the defect sits in the
but captures and emits its charge from/to the silicon (Si)
conduction or valence band respectively. This is the situation in Si-based electronics with a
gate oxide. The Si/
band offset is assumed as 4.5 eV in our
calculations.
3.1.2 Formulation of the Model Using Potential Energy Surfaces
Figure 3.2: Illustration of the four-state defect model from [YWJ1] showing a schematic presentation of a cross-section of the potential energy surface along a configuration coordinate (CC) for an example defect. The schematic
serves to illustrate the energy parameters needed for calculating the rates of vibronic transitions described using non-radiative multiphonon theory (1 2
as 2
1
) and thermally activated transitions described using transition-state theory (2
2 and 1
1).
Our model for NBTI is based on potential energy surfaces for a defect in its neutral (blue lines) and positive (red lines) charge state [18]. As explained in Section 2.2, the minima of the potential energy surfaces correspond to the stable and metastable states of the defect structure. The defect can exist in two different structural states, where each again can be either neutral or positively charged. The charged states affect the device characteristics of the MOS transistor, the neutral states are invisible to electrical measurements. Even though each state of the model is related to a specific atomic configuration of a defect, the model itself is formulated in an agnostic fashion so that it is suitable for different defect candidates. For each defect candidate, the microscopic configurations and thus the PES will be different.
Fig. 3.2 shows the schematic representation of the four-state model using PESs. In this figure, the energy parameters defining the PESs are depicted. Note that two transitions in this model are purely thermally activated (see Section 2.2.4) and two are modeled using NMP-theory (see Section 2.2.1). In this first order approach, only the NMP transitions are bias-dependent. The model has 13 characteristic parameters which, for one specific defect, can be extracted from measurement by fitting the measurement data from Fig. 3.1, resulting in Fig. 3.3.
In principle, the data for the fixed oxide trap (Fig. 3.1 left) could be fit reasonably well assuming only a three-state model, whereas
for the switching oxide trap (Fig. 3.1 right) the assumption of a second metastable state is necessary. This is due to the two possible paths in this model to get from state to
and vice versa (
and
). For the fixed oxide trap one of these paths is
energetically unfavorable and therefore blocked, resulting in effectively three available states. For the switching trap, on the other hand, the preferred path can switch depending on the conditions, causing the voltage (field) dependence of
for these defects [132].
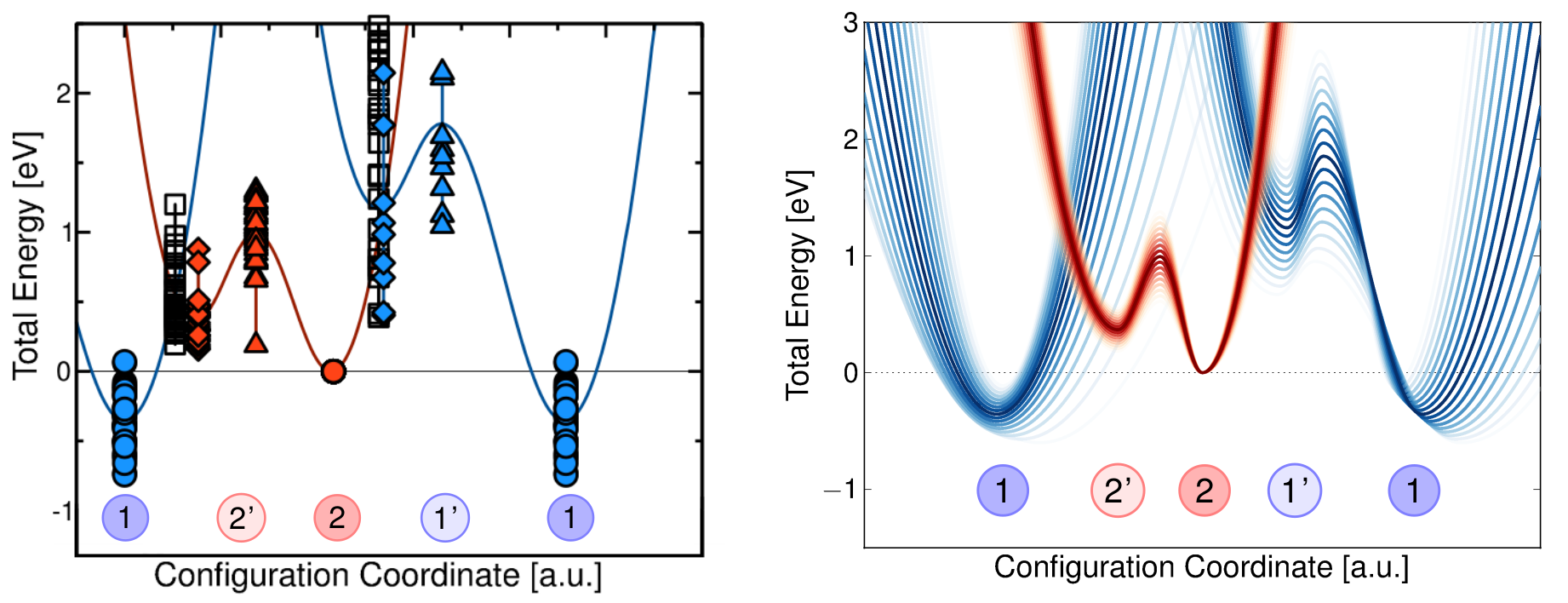
Figure 3.4: Left: Diagram illustrating the distribution of the potential energy surface parameters shown in Fig. 3.2 for 35 defects extracted using TDDS [YWC2]. The
energies are calculated relative to the valence band edge of Si and plotted relative to the energy of state .
Right: Schematics of possible CC diagrams when considering the aforementioned deviations [YWJ1]. In addition to the mean curve, the envelope curves of the potential energy surfaces for calculated standard deviations of the characteristic parameters are
schematically shown up to a deviation of
. From this figure, however, one cannot di-
rectly deduce the distributions of the particular model parameters as shown in the left figure. Due to state
being the reference energy, the height of the curves at the barrier
, for example, does not only depend on
but also on
and
of the states
and
. The reasons for taking the positive state
as a reference value in these plots are discussed in Section 4.3.2
and Appendix A.4.
Due to the amorphous nature, each defect studied in TDDS measurements has a different set of parameters. Fig. 3.4 schematically shows possible combinations of PESs that could arise from the parameter deviation
obtained by TDDS studies of 35 defects in six pMOSFETs (WL =
150 nm
100 nm, 2.2 nm SiON [YWC2]). One can clearly see that there is a large
variety of possible combinations of energy barriers and therefore of PESs. Thus any comparison of model parameters with experiment has to be carried out by statistical analysis.
All but two of the characteristic parameters can also be obtained by DFT calculations (see also Section 4.3). When the corresponding PES of
a defect candidate is calculated theoretically by DFT in a-SiO, the amorphous nature of the host material also causes the
parameters to vary for different defects of the same kind. A comparison of the parameter distributions obtained from the experiment and by the calculations can, therefore, help to identify the defect possibly responsible for NBTI. The corresponding calculations and defect
candidates are presented in Chapter 4.
3.2 The Hydrogen Release Model
Experimental results and theoretical calculations have led to the development of an NMP four-state model to explain the NBTI degradation. However, as mentioned in the introduction (see Section 1.4) research indicates that NBTI degradation consists of two components [57–60]. One distinguishes between the recoverable component (RC) and a more or less permanent component (PC). The exact
definition of this phenomenon is rather challenging since it has been shown that charged defects not only recover, but can also be annealed at higher temperatures [59, 61–65], or by voltage sweeps [YWC1]. This implies that there might not be an actual
permanent component. Rather the PC is also recoverable, though at considerably larger timescales than the RC. Since the two components cannot be measured separately the extraction of the PC is rather difficult since it is usually overshadowed by the RC. The
most straightforward approach would be to wait until the recovery of has leveled at a plateau. However, due to the
very large timescales involved (even for short stress times), this is very impractical. Recently a pragmatic definition of the PC was suggested [YWC1, YWC3] in which after stress the device is ramped into accumulation several times, thereby removing a lot of trapped
charges typically associated with the RC [134]. In this pragmatic approach, the remaining degradation is then defined as PC.
The H release model introduced below tries to interlink the PC with H being released from the gate of the MOSFET into the oxide material and subsequent H movement through the material. It was inspired by findings indicating such an H release and will be discussed in the following.
3.2.1 Experimental Evidence for Hydrogen Release
There are numerous reports of H release during stress in the literature [135–140]. Furthermore, several H-related observations have been reported [YWC3]:
-
• H moves towards the channel side during stress and back again during recovery, as has been shown in nuclear reaction analysis [140].
-
• Following BTI stress dopants inside the channel can be passivated by H released from the oxide [135].
-
• During BTI stress the noise has been reported to increase [23, 141]. After a high-temperature treatment (bake) in accumulation, this noise could be considerably reduced. During such a bake step H, which could have built defects close to the channel during stress, could be moved back towards the gate side [YWC1].
-
• Very strong Si–H bonds (
2.5 eV) are broken during NBTI stress [142].
-
• In samples with very low H concentration, it was observed that BTI stress actually leads to passivation of Si–H bonds. However, this would also be consistent with H release from the oxide [17].
Based on these observations, recently a model for H transfer within the defect oxide was formulated. Since all the experimental features cannot be explained by transfer only, also H release from the oxide was included in this model. This H release model is presented in the following.
3.2.2 Formulation of the Model
Figure 3.5: The proposed gate-sided H release mechanism from [YWC3]. At the gate side, a proton is trapped (A). During stress, the trap level can be shifted below the Fermi level (B), which makes it possible for the proton to become neutralized. This neutrally charged H atom can now be released by overcoming a barrier and move towards the channel side (C) and becomes trapped again at a new trapping site (D). The empty trap site can potentially be refilled by H released from the gate. This process should be strongly temperature dependent.
Figure 3.6: 1D schematic of the H release model from [YWC3]. All over the oxide, there are potential trapping sites for the H. A trapped H can either become positively charged via an NMP transition or overcome a thermally
activated barrier to become interstitial. Due to the high diffusivity of H, the exchange to a new trapping site is very fast and therefore not rate limiting [143]. The gate side acts as an additional H
reservoir. Assuming that H is bound there in the form of Si–H bonds, the release barrier is 2.5 eV [144, 145].
Figure 3.7: Long-term degradation data fitted using the H release model from [YWC3], in which a device is cycled between two different voltages and different temperatures. The evolution of the remaining permanent component (P) of degradation is shown over time. Measurements were always carried out at 200 °C (yellow dots). In particular, the H released from the reservoir can explain the additionally created defects at higher temperatures. Even though the model without the assumption of H release from the gate is able to explain the measurements up to phase E, it would fail as soon as obviously new defects are created in the long high-temperature stress phase F.
It was shown previously that it is in principle possible to model the experimentally seen behavior using the above described NMP four-state model, extended by a double well model for the permanent component [69]. However, as already mentioned in the
introduction, this modeling attempt was not entirely satisfactory, since it does not involve fundamental physical parameters (see Section 1.5.3). An H release model as suggested in [YWC1, YWC3] (see Fig. 3.5 and Fig. 3.6) is able to
cover the observations listed above while also offering a new modeling perspective to the permanent component of NBTI. The proposed gate-side H release mechanism is shown in Fig. 3.5. During stress, a proton
trapped at the gate side can become neutralized and released when overcoming a barrier. The now interstitial neutral H then moves towards the channel side and become trapped again at a new trapping site. The empty trap site can potentially be refilled by H released from
the gate. This process is typically associated with breaking Si–H bonds and therefore a rather high barrier 2.5 eV [144, 145]. At elevated temperatures this barrier can be overcome,
explaining the additional defect creation at 0 V “stress” experiments reported in [YWC1, YWC3] (see also Fig. 3.7). A 1D
schematic of the model is presented in Fig. 3.6. Note that due to the high diffusivity of H the exchange to a new trapping site can occur very fast and therefore is not rate limiting [143].
Results of a long-term degradation experiment is shown in Fig. 3.7 [YWC3]. In this experiment the device is cycled between two gate voltages (0 V and −1.5 V) and two elevated temperatures (250 °C and 350 °C) over four weeks. For these experiments, the pragmatic definition of the PC mentioned above was used. The steps in the phases A and C correspond to baking steps which should actually anneal defects [59, 61–65]. It is, however, clearly visible that new defects seem to be created. This becomes clear in the long stress phase F, in which new defects are created constantly. An anneal seems to take place in phase E, however, the defects seem to be easily recharged at the start of phase F. The findings seem to be consistent with the proposed H release model. Note that the model without the assumption of H release from the gate is able to explain the measurements up to phase E. However, this could not explain the defect creation in the long high-temperature stress phase F. Therefore, H release from the gate over a rather high barrier has to be assumed.
4 Statistical Comparison of Defect Candidates
As already mentioned in Section 3.1.2, the parameters obtained from measurements deviate strongly from defect to defect. This is due to the amorphous nature of the oxide. Whereas in a crystalline structure the local environment is identical at each unit cell and so the defect’s chemical environment is too, in an amorphous structure the conditions are different at each atom and therefore for each defect.
In this chapter in order to judge whether a particular defect candidate is suitable to explain the behavior seen in measurements, the NBTI four-state model is used as the basis. The parameters in this model are shown in Fig. 3.2 and can be extracted from measurements as well as from DFT calculations. These calculations were carried out using amorphous silicon dioxide (a-) clusters as the host material which naturally also causes
statistical variations in those calculations.
In the following, the characteristics and creation of the used host structures are described. Then the three investigated defect candidates are presented: the oxygen vacancy (OV), the hydrogen
bridge (HB) and the hydroxyl-E center (H-E
center). Finally, a statistical comparison of the parameters as described above is carried out,
showing that the OV is not a promising candidate to explain NBTI.
4.1 Creation of Amorphous SiO Structures
Structures
The calculations described in this chapter make use of both classical force field and ab initio calculations to generate a- structures. The procedure used to create these structures
is described in detail in the work of El-Sayed et al. [79, YWJ2]. The ReaxFF force field [146] implemented in the LAMMPS code [147] was used to generate 116 periodic structures of
a-
, each containing 216 atoms. Starting from a
-cristobalite configuration, the structures underwent molecular dynamics simulations in which they were melted and quenched. In these simulations the temperature was raised to 7000 K to melt
within the ReaxFF force field, followed by a quench to
0 K at a rate of 6 K/s. A barostat was used to keep the pressure fixed at 0 bar. Using this method 116 defect-free continuum random network a-
structures could be created. The obtained densities of
the a-
structures ranged from 1.99 to
2.27 g/cm3, with an average of 2.16 g/cm3, which agrees with the range of densities known for a-
[148, 149].
The DFT calculations in this work were all carried out using the CP2K code [150] (see Section 2.1.1). As discussed in Section 2.1.4 and Appendix A, in order to minimize the errors in the energy levels and band-gaps, the non-local, hybrid functional PBE0_TC_LRC (see Section 2.1.4), was used in all calculations. Further parameters of interest used in the calculations are:
-
• A cutoff radius of 2.0 Å for the truncated Coulomb operator. [97]
-
• A double-
Gaussian basis set with polarization functions [151] in conjunction with the Goedecker-Teter-Hutter (GTH) pseudopotential. [152]
-
• Cell vectors were not allowed to relax from their ReaxFF values.
To reduce the computational cost of non-local functional calculations, within the CP2K algorithm the auxiliary density matrix method (ADMM) is applied [98] (see Section 2.1.5). The geometry optimizations all use the Broyden-Fletcher-Goldfarb-Shanno (BFGS) [153–156] algorithm to minimize forces on atoms to within 37 pN (2.3 × 10−2eV/Å) [YWJ1].
Using these settings the structures described above first underwent a geometrical optimization. The calculated structural parameters of the created amorphous structures including the average structure factor are discussed in [79, 157]. It was shown that optimized structures agree very well with the experimental data, indicating that the medium and long-range order of the models is well described by these models. Therefore, in this work, these models were used as host structures in which the defect candidates described in the following were created.
4.2 Defect Candidates
Defect studies in crystalline have already investigated many possibilities of defect
candidates which could explain the NBTI behavior in measurements [103, 158, 159]. The most promising were the OV and the HB defects, which both showed the sought after four-state behavior [67,
160] and were therefore of interest to be studied more closely also in a-
. Studies of defect candidates in a-
are, however, rare in literature [79, 161–163]
Additionally, there is one defect candidate of special interest that does not exist in crystalline
: the hydroxyl-E
center (H-E
center), also showing the desired features. In the following, these three defect candidates are
investigated.
Figure 4.1: Atomic configurations corresponding to states 1, 1, 2
and 2 for the oxygen vacancy (OV, top) hydrogen bridge (HB, middle) and the H-E
center (H-E
, bottom) from [YWJ1]. H atoms are shown as silver, Si atoms - yellow and O atoms - red. The
turquoise bubble represents the localized highest occupied orbitals for the neutral charge states and the lowest unoccupied orbital for the positive charge states. Upon hole capture, the defect can go into state 2
and the Si atoms move closer together in all the defects. Depending on the gate bias, the
defect either goes back to state 1 or eventually into the positive state 2 or the neutral state 1
, where the right Si has moved through the plane of its three O neighbors, forming a puckered
configuration by bonding to a neighboring O on the right.
4.2.1 Oxygen Vacancy
The most and best-studied defect in is most likely to be the oxygen vacancy (OV). The OV
forms when a two-coordinated oxygen (O) atom in the amorphous
network is missing. The missing O atom causes the two
Si atoms neighboring the vacancy to form a bond accompanied by a very strong relaxation of the surrounding
network (see Fig. 4.1 OV
).
When the OV traps a hole, it converts into a paramagnetic E center, the most abundant dangling bond center in a-
[164] which has been investigated in a number of papers
[159, 161–163, 165–178]. This defect has several configurations, dependent on the local environment [159, 161–163, 172–178].
The most important metastable configurations in the scope of this work is formed when the Si ion with the hole moves through the plane of the three neighboring O atoms and is stabilized by the interaction with another, so-called back-oxygen ion [159, 172–174] (see
Fig. 4.1 OV ). This configuration is often referred to as the E
center, the back-projected, or the puckered configuration1. This configuration can be metastable in the positive, as well as in the neutral
charge state, providing the four required states for this defect to be relevant for the defect model described in Section 3.1. However, the back-oxygen ion is not always in the right position in a-
to stabilize the configuration
(see discussion in [174, 175]). As a consequence, this configuration does not exist at every Si site in
a-
. In the set of 116 a-
structures described above a stable four-state
configuration as shown in Fig. 4.1 was only found in
6% of the possible defect sites [YWJ1]. The resulting maximum possible density
of possible four-state defect sites is therefore 2.6 × 1021/cm3. Unlike the two defect candidates below, for the OV the positively charged state is the one holding an unpaired electron. Therefore this state should be the electron spin resonance
active configuration.
4.2.2 Hydrogen Bridge Defect
The hydrogen bridge (HB) forms very similarly to the OV, but in the case of the HB, instead of the bridging O atom, an H atom is present. Seemingly, the likely formation mechanism is when an H
atom is trapped in an already pre-existing OV. In order to study the interactions of H with vacancies in a-, in [YWJ1] all O atoms in a single a-
structure were removed one by one to create 144
configurations with one OV each. For DFT simulations the HBs were constructed by replacing one two-coordinated O atom by an H atom followed by geometry optimization. This results in an asymmetric defect structure in which the H is closer to one of the vacancy’s Si
atoms (Fig. 4.1 HB
). The neutral HB consists of a short Si–H bond and a longer-range Si- -H interaction, where - -
indicates a non-bonding interaction. The short Si–H bond averages at 1.47 Å, ranging from 1.44 to 1.51 Å. The distance of the Si- -H interaction averages at 2.21 Å and ranges from 1.74 to 3.13 Å. This indicates that the shorter bond is
a strong chemical bond while the longer range Si- -H interaction is weak and strongly influenced by the amorphous environment [YWJ1] (see also [179] for further discussion). The asymmetry of the neutrally charged HB is caused by the unpaired electron of the defect,
which is localized on the Si atom not possessing the H (see Fig. 4.1).
Like the OV, the HB also has a puckered configuration. However, the situation for the HB is overall slightly different since the unpaired electron is present in its neutrally charged state. It is, however, capable of forming a puckered configuration in its positively
charged state and a secondary configuration in the neutral state
(see Fig. 4.1 HB). In contrast to the
puckered configuration of the OV, in this case, the Si atom with the unpaired electron is inverted through the plane of the three neighboring O ions with a dangling bond facing towards a back-oxygen ion (a so-called back-projected configuration of the Si dangling bond).
All four configurations of the HB are stable in 55% of the investigated structures, this is a density of possible four-state defect sites of 2.3 × 1022/cm3 [YWJ1].
4.2.3 Hydroxyl-E Center
Center
The hydroxyl-E center (H-E
center) forms when an H atom interacts with a two-coordinated O atom, thereby breaking one
of the Si-O bonds in the neutrally charged state. In [YWJ2, 179] it is stated that, for this defect to form, a strained (
1.65 Å) Si–O bond has to be present in the
a-
network. This criterion is fulfilled for
2% of the Si atoms in our structures [179]. Consequently the H-E
center does not exist in
-quartz and this defect only forms at particular sites in amorphous structures.
However, in this work, it will be shown that the H-E
center can also form for smaller bond distances (see Chapters 5 and 6). Briefly, it resembles a
three-coordinated Si atom with an unpaired electron [172], facing a hydroxyl group (Fig. 4.1 H-E
), a configuration that is referred to as E
center. The Si dangling bond introduces a single-electron level located
3.1 eV above the a-
valence band. The value range from 2.40 to 3.90 eV, thus for some configurations the defect level is almost resonant with the top of the Si valence band [YWJ1].
Like the two previous defect candidates, the H-E center also has a stable puckered configuration in the positive state
and a stable back-projected configuration in the neutral charge state
(see also Fig. 4.3). The back-projected configuration is formed when the three-coordinated Si moves through the plane of its O neighbors and weakly interacts
with a two-coordinated O. The hole in this configuration is highly localized on the inverted Si. This configuration is shown as configuration
in Fig. 4.1 (H-E
). Thus, the H-E
center also exhibits the bi-stability required for the four-state NMP model (
7% feature all four states [YWJ1]). In [YWJ1] 61 a-
structures were studied and a density of
possible stable four-state defect sites of 2.8 × 1019/cm3 was determined. This, however, is only true for the estimation of the strained-bond precursor which might be questionable because of the findings from Chapter 6, in which it will also be shown that a
positively charged H atom (a proton) can bind to nearly every two-coordinated O atom, forming a hydronium-like structure. For the neutral and negative charge variant of this defect, several different configurations arise (see Chapter 8.2). The H-E
, therefore, actually is only one member of a family of possible defects when H interacts with
an a-
network.
4.3 Statistical Analysis of Various Defect Parameters
The structural disorder in a- results in wide distributions of defect parameters in
experimental measurements as well as in DFT calculations. Thus, linking the experimental and theoretical data requires comparing their statistical properties. In this work, this was done using the four-state model (see Chapter 3.1) as a basis. On the one hand, the corresponding parameters shown in Fig. 3.2 are extracted from TDDS measurements. On the other hand, those
parameters are calculated theoretically for several defects of the same kind in DFT calculations in the above-mentioned a-
structures. If the distributions of parameters match those
for a particular defect candidate, we consider it to be a likely candidate for the experimentally observed charge capture and emission effects.
The NMP four-state model requires 13 parameters, of which the 11 shown in Fig. 3.2 can be extracted from DFT calculations [YWC2]. These include the thermodynamic defect levels, energy barriers, and defect relaxation energies. The two parameters which cannot be calculated by DFT are:
-
• The distance of the defect from the
-Si interface (depth of the defect), which is actually responsible for the step heights in RTN and TDDS (see Section 1.2). For single defects it is taken as a fitting parameter. Otherwise, for simplicity, a depth of 1 Å was assumed for all defects.
-
• The capture cross-section, eq. (2.30), in which the electronic matrix element requires the overlap of the electronic wave function of the initial and final atomic configurations. For our application for the gate oxide of a MOSFET this would include the states in the silicon substrate (conduction and valence band) [160].2
2 For thermal transitions the respective counterpart is the attempt-frequency (see eq. (2.36)) which fulfills the same function in the rate equation (see Section 2.2.4).
4.3.1 Computational Costs for Different Parameters
The required computational resources to determine these parameters in Fig. 3.2 vary widely between the different types. In general, one can distinguish three types of calculations by their computational effort and time. They are associated with different kinds of parameters:
-
• Single-Point Calculations for obtaining parameters when the underlying atomic configuration is already known. Depending on the approximation of the PES (see Chapter 7), only a few energy values have to be computed along the reaction coordinate in order to obtain the part of the PES needed. The required DFT calculations are referred to as “single-point” calculations, meaning that the energy is computed without additional optimizations, regardless of whether the structure is in an energetic minimum or not. The required computational costs are therefore rather low. On the clusters used in this work (VSC1, VSC2, and VSC3 [180]) these calculations typically used
core hours and can be completed within a few minutes because of parallelization.
-
• Geo-Opt Calculations for obtaining parameters associated with the equilibrium positions of the states and metastable states. These values are obtained by geometrical optimization of the structures from an initial guess. The geometrical optimization consists of several single-point calculations until the forces in DFT are minimized. These calculations typically need
core hours on the clusters, and can, therefore, be completed within a few hours when running in parallel on several cores.
-
• NEB Calculations for finding the minimal barriers for structural change between the stable and metastable states of the same charge state. In the four-state model (see Section 3.1) this refers to the transitions
or
respectively, i.e. the barrier heights
and
. Furthermore, all volatility barriers in Chapter 5 and all H hopping barriers in Chapter 6 are determined this way. These parameters have to be calculated using the NEB algorithm (see Section 2.2.5). This requires the parallel optimization of a whole reaction path and typically required
10 k core hours and takes up to a few days on the mentioned computer clusters. These are therefore by far the most expensive calculations.
For some of these properties, large data sets could be obtained. For the mentioned computationally very costly barriers the statistics presented in the following cannot be assumed to be rigorously representative of the entire population of each defect in a-. They can, however, offer an idea of whether the
parameters are in the right range to be able to explain the observed experimental behavior.
4.3.2 The Thermodynamic Trap Level
Figure 4.2: Schematics of the link between the PES, the band diagram and the thermodynamic trap level (). For hole trapping
(blue) is defined as the difference between the minima of
the positive and neutral PES. The minimum of the positive PES is assumed as a reference, fixed at the valence band edge. The
alignment of the PES relative to each other, transitions and interaction with an electric field is discussed in the more detailed Fig. A.2 in Appendix A.4.
The thermodynamic trap level (or thermodynamic charge trapping level), , is the fundamental parameter that decides which trap
can be charged for a combination of certain stress and recovery voltages. It is, therefore, the most important parameter for identifying defect candidates.
is defined as the difference of the minima of the two
PES involved in the charge capture or emission process (see Fig. 4.2). For the hole trapping transitions, the minimum of the positive PES is assumed as a reference, fixed at the valence band edge.3
The interaction of the PES with an electric field shifts the PES relatively to each other. A more detailed figure linking the band diagram to the PES and also for the case of an applied electric field is given in
Appendix A.4 in Fig. A.2. The minimum of the positive PES acts as a reference point throughout this work. This is the reason for the state 2 being the
reference point in Fig. 3.4.
It should be noted that the alignment of DFT energies obtained for different charges is not unambiguous, which is why the chosen alignment method considerably affects . The alignment methods and corrections are discussed
in Appendix A. For the calculations discussed in the following, especially the band-gap error (Appendix A.3) is of importance as the justification for an adjustment made in the statistics presented in Fig. 4.4.
of a suitable defect candidate should lie close to the
valence band edge. Then the NMP-barrier for capturing and emitting a hole from and to the valence band is of the right order of
magnitude. This means that NBTI defects have an
in the range of
−1.0 eV to values just slightly above
. The electric fields originating from the applied operating
voltages shift the PES relative to each other, thereby changing the energetically favorable charge state (see Fig. A.2). The above estimation for the range of
is valid for typical operating voltages. Higher values of
would render the defect permanently positive, lower
values permanently neutral.
4.3.3 The Puckering Transitions
As mentioned in Section 3.1.2, the different defect behavior in Fig. 3.3
(“effective three-state” or “effective four-state” defect), is attributed to whether or not the barrier can be overcome under measurement conditions. In the following, we will refrain from the
distinction whether the final state is a puckered or a back-projected state of the respective defect. For the NBTI four-state model this distinction is irrelevant since it is only of importance if two stable
states exist. Both realizations will be referred to as “puckered” states. The respective transition will be referred to as “puckering transition” (see Fig. 4.3) in which the three-coordinated Si atom passes the plane of its
remaining three O atoms and interacts with a forth O atom on the other side. It is clearly visible that during such a transition the charge stays attached at the Si atom. This means that the transition can be treated as adiabatic in DFT.
Figure 4.3: Puckering transitions for the positively (top) and neutrally (bottom) charged hydroxyl-
E center. Beneath the figures, a schematic showing the approximate position on the PES is given.
The passage of the Si atom through the plane of its neighbors can be seen well for both charge states. The turquoise bubble represents the localized highest occupied orbitals for the neutral charge states and the lowest unoccupied orbital for the positive charge states. It is
clearly visible that during such a transition the charge stays attached at the Si atom.
The puckering transitions are the transitions between the stable and metastable states of the NBTI four-state model. The existence of these states allows for the charge capture and emission time constants to
be independent of each other, which is a very important feature of the model, needed to explain the experimental observations [3]. The link between the barrier heights and transition times of such purely
thermally activated transitions are given in eq. (5.1) and Fig. 5.2. The experimental results suggest transition times on the order of microseconds to seconds, which would refer to barriers in the range of 0.4 - 1.0 eV. Higher barriers would not be overcome in the experiment. Lower
ones, on the other hand, are also problematic. Since the experiments indicate the existence of a stable and metastable state, the barriers have to be at least high enough to allow transition times larger than the measurement resolution. For lower barriers, the two states would
become indistinguishable in the experiment and would not appear as separate states anymore. Furthermore, for a suitable defect candidate, the barrier
should be considerably higher than
to explain the different behavior (“effective three-state” or “effective four-state”
defect) in Fig. 3.3.
4.4 Results of the Statistical Comparison
Figure 4.4: Top: Distribution of the thermodynamic charge trapping levels from [YWJ1], , (see Section 4.3.2).
The top of the Si valence band is set to zero. Note that all defects close to the valence band of Si,
(Si), will contribute to RTN in a pMOS. Clearly, the OV is
too low in energy, while both the HB and the H-E
center are in good agreement with the data inside the experimental window.
Bottom: The experimental and calculated barriers for the various transitions in the four-state model. The parameters are shown on the diabatic potential energy diagram in Fig. 3.2. While overall good
agreement is obtained, the theoretical barrier
is too small in general. The defects ap-
pearing with negative
are 2-state defects at the bor-
der of our experimental window.
It should be noted that in order to account for the band-gap-error in DFT, a −0.4 eV energy shift was used for these parameters.
The thermodynamic trap level and the barriers for the puckering transitions can be considered the most important parameters to judge whether or not a defect candidate is suitable to explain NBTI. The defect candidates in question have to show very high accordance in the parameter distributions between the results obtained by DFT calculations and the parameters extracted from the experiment. Accordance has to be achieved in all of the parameters, otherwise, the theoretical defect behavior would be very different from the experimental one.
The accurate assignment of levels in DFT always needs a reference energy (see also Appendix A). In our case, one can relate the defect levels to (Si) calculated using the same hybrid functional.
However, this would place 60% of our HBs and 75% of the H-E
centers above
(Si) and thus render them permanently positive under
NBTI conditions. In order to retain a larger fraction of our defect population (58% HB and 50% H-E
) and improve our statistics, we introduced an energy correction of −0.4 eV,
corresponding to
50% of our
band-gap-error (0.8 eV [79], see also Appendix
A.3). Applying this adjustment, the HB and the H-E
center, are in the right energetic position below
(Si) [YWJ1].
It should be kept in mind that the distributions obtained from the DFT calculations are spread out over a wider range, compared to the values deduced from experiment. This is due to the limited timescales for defect capture and emission times accessible in the experiment. However, also the experimental data suggests that the defect distributions are much wider than what can be captured in our TDDS window [64, 181]. The results of the comparison are presented in Fig. 4.4. A closer evaluation of the shown distributions leads to several findings and conclusions:
-
• The distribution of
for the OV is much too deep to be able to explain experimental data (see Fig. 4.4 Top). Similar findings have already been reported in crystalline
structures [YWC2, 56]. The possibly large distribution in a-
is not able to make the OV a possible defect candidate.
-
• The distributions of
of the HB and the H-E
are generally in reasonable agreement with the distributions extracted from the experimental data. However, it has to be noted that the energy correction mentioned above shifts the parameters slightly towards the measurement window.
-
• The energy barrier distributions of the HB and the H-E
are also generally in reasonable agreement with the energy barrier distributions extracted from the experimental data as shown in Fig. 4.4 (bottom). The most significant deviation here is observed for the barriers between states 2 and 2
,
and
, respectively.
The barriers and
determine the transition times between
the stable and metastable positive state and hence also the hole emission time constant. The calculated mean value is notably smaller than the experimental values, on average by
0.5 eV. A considerable part of the calculated barriers is so low that the transition under measurement conditions would be faster than the typical measurement resolution. Hence, for those barriers, it
would be impossible to resolve two distinct states and they would not satisfactorily explain the full observed NBTI behavior. This is the main shortcoming of the HB and the H-E
as NBTI defect candidates. Whether this is an artifact of our bulk amorphous oxide
structure or evidence for a different microscopic nature of the defect remains to be clarified. It should be noted that the current modeling approach does not include a possible dependence of the thermal barrier
heights on the electric field. Although recent modeling attempts did not suggest a considerable effect when the electric field was taken into account in the DFT calculations, this dependence should be
subject to further investigations.
4.5 Conclusions
From the results above it is clear that the OV is a very unlikely candidate for explaining charge capture and emission in our TDDS experiments. The statistical properties of the HB and the H-E center, on the other hand, give a good match for the majority of the parameters of the
four-state model. The main shortcoming of both these defect candidates is the not entirely satisfactory accordance between theoretical calculations and experimentally deduced values for the barriers
and
. A considerable part of the theoretically
calculated values is too low to properly separate the positive stable and metastable state. It is not possible to deduce from this data whether one of them is more likely than the other since the
statistical properties are very similar for both. Therefore, it cannot be ruled out that both defects could contribute to the experimentally observed charge capture and emission events.
However, the experimental observations also show that many defects tend to dis- and reappear during measurement cycles, which is referred to as volatility. This effect will be discussed in more detail in the following chapter. It will be shown that the proposed mechanism responsible for volatility is very unlikely to occur for the HBs, therefore further supporting the H-E center as a defect candidate responsible for NBTI.
5 Volatility
As shown in the previous chapters, RTN and TDDS analysis have provided a deep insight into the trapping dynamics of oxide defects. However, one additional feature that is observed during these measurements has not yet been addressed in detail. As mentioned in the introduction, defects have been found to frequently disappear in the measurements. Many of them reappear after a certain amount of time and measurement cycles (or heat treatment), as shown in Fig. 5.1 [44, 67, YWC4]. Some, however, remain inactive (see Fig. 1.5). This so-called volatility is not a rare event, but can potentially occur for a majority of the defects, particularly when electrons are injected into the oxide [YWC4]. A consistent model of oxide defects must, therefore, not only describe their behavior when electrically active but also provide an explanation for their disappearance and reappearance during measurement cycles.
In this chapter it will be investigated if the volatile behavior can be explained, assuming that the responsible mechanism is the hydrogen (H) atom moving away from the actual defect site. Therefore, the four-state model presented in Section 3.1 will be extended to account for an inactive state. The most important parameter to judge whether or not the proposed mechanism is suitable to explain the experimentally observed volatility behavior, are the barriers that have to be overcome during the H relocation. It will be shown that these barriers make the hydrogen bridge (HB) a very improbable candidate for the suggested volatility mechanism.
5.1 Volatility in Experiments
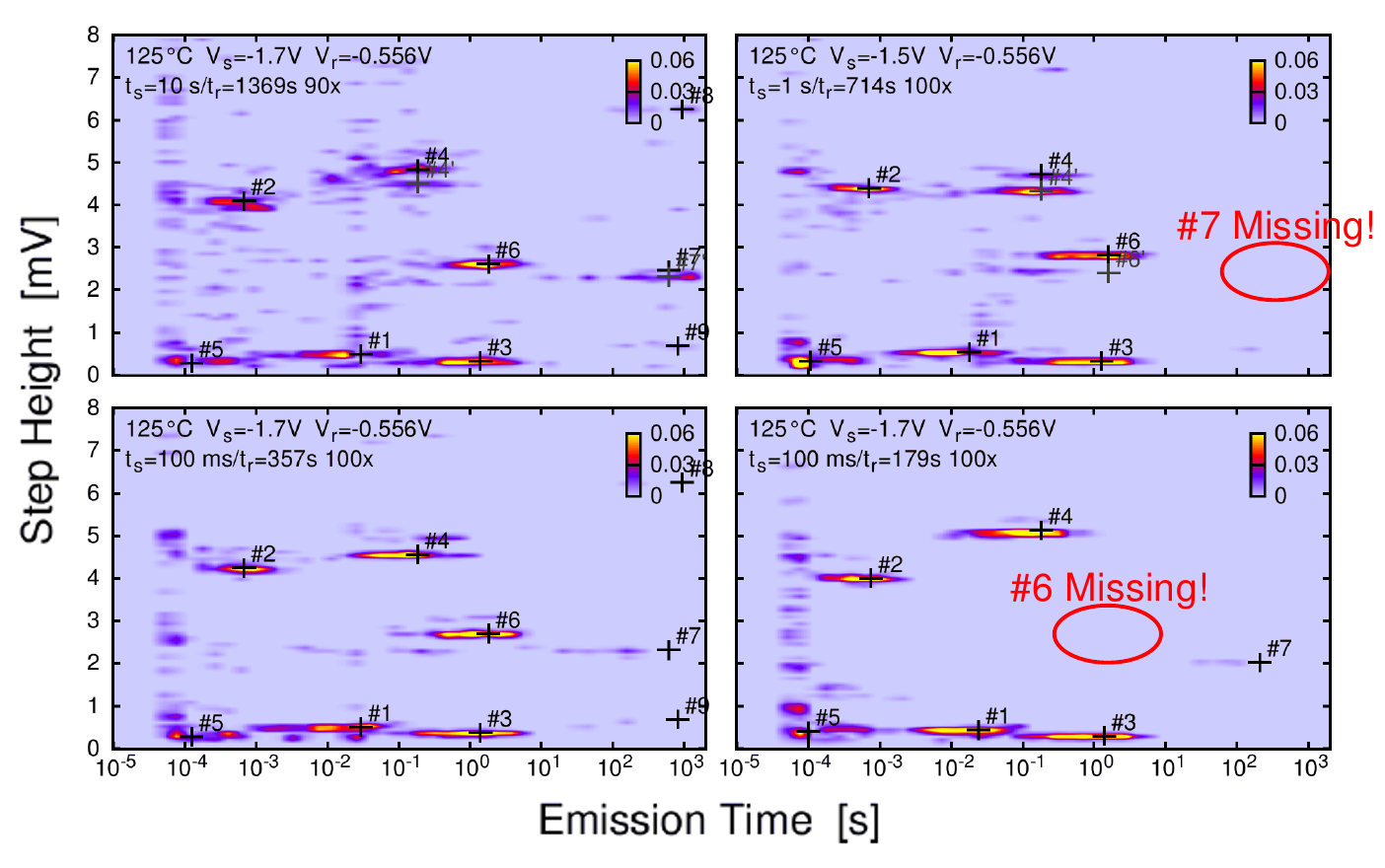
Figure 5.1: Top: Defects tend to dis- and reappear in TDDS measurements. In the shown examples defects disappeared during the experiments from one measurement cycle to another [44]. The spectral maps (see also 1.2) were all taken on one device, but at different times during an experiment with several stress- and recovery cycles. It is clearly visible that in two spectral maps the defects #6, or #7 respectively, are missing. Note that defect #7 later reappeared in the measurement. Bottom: Defects can dis- and reappear several times during TDDS measurements, especially if the measurement is taken out for a long time. Here the results for three selected defects which were monitored over three months are depicted [YWJ1]. The plots show when the defect is electrically active or inactive (volatile). Occasionally, the experimental conditions did not allow for an observation (“blind” phases), for instance during a long high-temperature bake around the beginning of the third month.
In our TDDS measurements, we observe time constants for defect signals disappearing in the volatile state, , in the range of hours to weeks (see Fig. 5.1). The upper limit is given by the measurement duration. The lower limit has not yet been rigorously tested. We speculate that a
as low as one second could well be detected for a defect
normally capturing and emitting in the microsecond regime. However, up to now, the lowest observed
has been
20 minutes. Assuming that the dynamics are determined by a thermally activated
rearrangement of the atomic structure, we are again dealing with a two-state process (active/inactive).
Similar to RTN and 1/f noise we can estimate the corresponding reaction barrier with an Arrhenius law [1, 3, 130] (see also Section 2.2.4). For this purpose we can rewrite eq. (2.36) as:
Assuming an attempt frequency of 1013/s [7, YWC2], the corresponding rearrangement barrier height
at room temperature should be about 0.90 eV.
This value only increases to about 1.09 eV for a
of one month. Of course, higher barriers can be overcome
when measuring at higher temperatures and for longer times. Due to the exponential dependence of eq. (5.1) on
and
even small changes of these values have a considerable influence on the corresponding value for
. In Fig. 5.2 an overview of several orders of magnitude of
and the corresponding values of
is given for different temperatures. This figure is meant
as a guide to estimate the order of magnitude of
from the barrier heights calculated in the following
chapters. To give an example:
for a barrier of 1 eV is on the order of hours at room temperature, of seconds at 100 °C and only of microseconds at 350 °C, given the assumption for
[7, YWC2].
Figure 5.2: Transitions barriers over volatility time constants for different
, when assuming an attempt frequency of
1013/s. Due to the exponential dependence of eq. (5.1)
on
and
even small changes of these values have a
considerable influence on the corresponding value for
.
5.2 The Extended NBTI Model
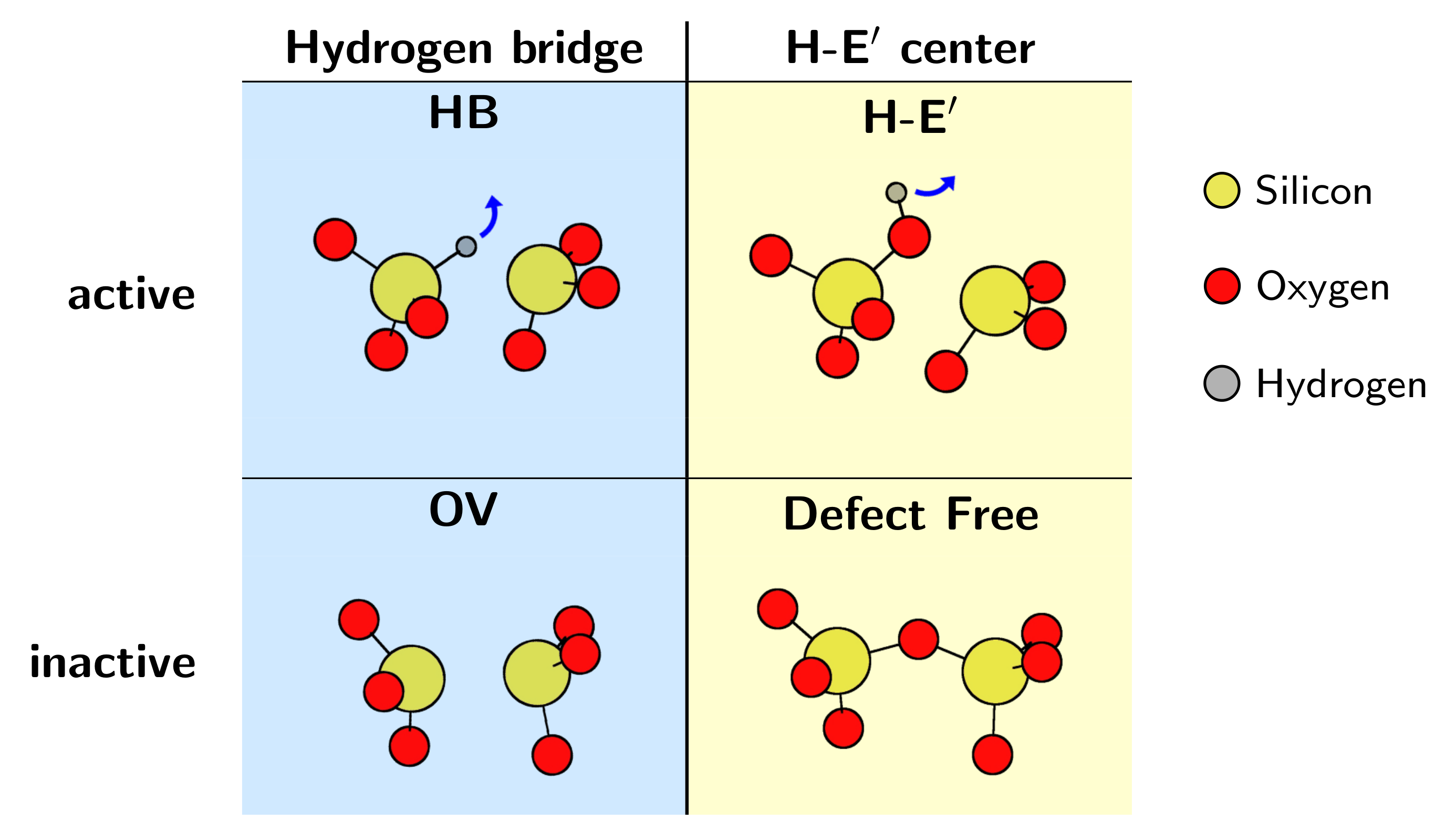
Figure 5.3: H relocation for HB and H-E center defect. The HB is transformed to an OV, which was shown to be an unsuitable defect
candidate in the previous chapter. The OV would be electrically inactive, thereby providing a suitable volatile state. For the H-E
center H removal results in a defect-free structure.
As was shown in Section 2.1, both the HB and H-E centers exhibit the bi-stability and the trap level positions favorable for RTN and NBTI
observed in Si MOSFETs. Since both of them contain an H atom and several publications have shown that H can be released during electrical stress [135–140], we investigated whether the dynamics of
the H atom could be a possible cause of volatility. Therefore, in the following, we consider the two H-containing defects in both the neutral and positive charged states.
Consider that the presence of the H atom in the HB moves its level into a more favorable position for hole trapping with respect to the OV. Thus losing H (transforming the HB defect into an OV) could take the defect out of the TDDS measurement window. This H
relocation corresponds to either a neutral H atom (H) moving away from the neutral defect state or a proton (H
) from the positive defect state. For the H-E
center, losing the H atom would result in a defect-free structure (see Fig. 5.3).
Figure 5.4: Examples of potential energy surfaces of two H-E center defects along the reaction coordinates between different states for a defect that can
become volatile starting from a positive charge state (top [YWJ1]) or from a neutral charge state (bottom). Possible transitions can occur by charge capture or emission (green arrows) or barrier hopping (purple arrows). The defect is electrically active when on the left side
of the plot (orange). When the barrier
is overcome, the defect is electrically inactive (grey) and is,
in general, not visible in the measurements (given certain conditions discussed in Section 5.4).
For the model described in the following, the configurations without H presented above will be referred to as state (in addition to states
and
of the NBTI four-state model, see Section 3.1). The two new volatile states that emerge are called
for the positive and
for the neutral charge state. In order to account for volatility, the four-state model is
supplemented by these two new states and their respective barriers. When starting from a four-state defect, there are four possible relocation reactions:
,
,
and
. These are all assumed to be purely thermally activated transition and their barrier height, therefore, can only be calculated by the computationally very costly CI-NEB method (see Section 2.2.5). It could
be shown that the transitions starting from the non-puckered states
and
are always lower in energy than for their puckered counterpart [YWC5]. To give an example:
the NEB calculations performed for the positively charged H-E
center all showed that the reaction
does not happen directly but rather via the path
for all calculated transitions. This is an important finding, also for the modeling of hydrogen hopping in the following chapter, since it indicates that this process is not possible when in the puckered configuration. However, it has to be noted that
the barrier
is in general relatively low in our calculations (see Fig. 4.4 (bottom) and Section 4.4).
Another statement from [YWC5] did however not hold true when more calculations for the neutral charged states were carried out. In [YWC5] it is stated that the neutral transitions are always higher in energy compared to
. It will be shown here that neutral transitions are possible too.
Therefore, in the following, both these transitions in the non-puckered configurations are considered for the volatility barrier.
The resulting extended model is schematically depicted in Fig. 5.4. Here it is assumed that the transition into the inactive state is (top) or
(bottom) respectively. This figure is an extension of Fig. 3.2 including volatility. Similar to Fig. 3.2, the transitions involving charge transfer are considered in the NMP model. The transitions between states of the
same charge are again assumed to be purely thermally activated as well as the volatility transitions
or
. As described in Section 2.2.2, the applied voltage moves the neutral (blue) and positive (red) parabolas relative to each other, thereby changing the barriers for the NMP transitions. Note that the defect in Fig. 5.4 (bottom) is a defect in which the state
is rather unlikely to be reached. In measurements it would, therefore, appear as a three-state defect (fixed positive charge trap) whereas the defect in Fig. 5.4 (top) should have the required barriers to act as a four-state defect (switching
trap), as described in Fig. 3.1.
Of course, it has to be considered that the H does not just disappear entirely, but rather relocates onto a neighboring bridging oxygen (O) atom. Due to the amorphous nature of the structure, however, the vast majority of the possible new locations do not favor the
creation of a new four-state defect. Thus it can be regarded as a volatile state. Whereas H always binds to the bridging O atom it relocates to, the situation for the H
is more complicated. The DFT results showed three different pathways for the H
in state
:
-
• The H
detaches from the bridging O atom in
and becomes interstitial (Fig. 5.5 bottom left). A systematic study described in Section 6.1 assumes that
41% of the H
would show this behavior.
-
• In
one of the bonds of the bridging O atom breaks, forming an H-E
center (Fig. 5.5 bottom center). The calculations in Section 6.1 suggest that
49% of the H
would form this configuration.
-
• The H
stays attached without breaking one of the bonds of the bridging O atom (Fig. 5.5 bottom right). This is assumed to be only possible if a different feature capable of capturing an electron is present nearby in the structure. Only
10% of the volatile states are suspected to be of this type.
For the latter one, the required electron capturing feature could be, for example, a silicon (Si) with wide O–Si–O bond angle [157], which is observed for the majority of those cases. Here, a bond was
considered broken if the Si–O distance is 2.0 Å, in accordance with [YWJ2]. However, a
Mulliken charge analysis [182] revealed that also for smaller bond distances the electron occasionally still sits at one of the two Si atoms associated with the defect (see for example Fig. 5.6 (top) and
discussion in Section 6.1). For the majority of the cases, the electron sits at a Si atom further away in the structure. This could be problematic in the DFT approach, since it means that during
the transition also a charge has to be exchanged with an atom further away, possibly violating the adiabatic approximation of DFT [183, YWJ3]. This could greatly reduce the possibility for such a transition to occur due to a very low overlap of the wave functions of the
involved states. However, note that only
10% of the possible outcomes are of this type (see Section 6.1), which will be referred to as ”stick” in the following. The statistics presented in this chapter were generated from three structures containing an HB defect and six structures containing an
H-E
defect. One of the H-E
structures shows nearly exclusively “stick”-configurations. This seems logical if a feature as described above and in [157] is present in the structure. On the other hand, it leads to an overrepresentation of this barrier type in the statistics presented in this chapter. This
should be kept in mind, especially for Fig. 5.8 and 5.9. However, this is irrelevant for the main conclusions in this chapter since they are drawn
from the lowest barriers. It will be shown further that the “stick”-configuration is rather associated with higher barriers.
Figure 5.5: Top: Schematic showing the relocation of the H for the case of the H-E
center. The H
moves from the defect site in state
(left) onto a neighboring bridging O atom (right). We name this new positively charged state
.
Bottom: When the state is charged neutrally three different possible states
have been found: the H
becomes interstitial (left), the H
causes one of the O-Si bonds to break (middle), forming a new H-E
center or the H
remains attached (right). The latter is only possible when the H can transfer its electron to an
electron-accepting site nearby.
In Fig. 5.5 the relocation is depicted for the example of the H-E center. The principle also holds true for the HB defect. The observation that there is
interstitial H
in our calculations contradicts a popular assumption that because of its negative-U
character1 [184, 185], it would never be thermodynamically favorable. However, the present DFT calculations show that interstitial H
can be thermodynamically
favorable in a-
. Here it also has to be noted that the
negative-U property is determined for a thermal equilibrium, it does not hold information about any possible metastable neutral configurations of H. Fig. 5.6 presents three examples of the
volatility transition
each with a different behavior in
. Different configurations along the minimum energy path calculated using the CI-NEB
algorithm (see Chapter 2.2.5) are shown illustrating the course of the transition. Beneath the figures, a schematic showing the approximate position on the PES similar to Fig. 5.4 is given. Note that the volatility transition in the upper two cases ends at a neighboring O atom whereas for the bottom example it undergoes a cross-ring hopping. The dependence of barrier heights on this
distinction is investigated in more detail in Section 6.2.
It should be emphasized that no correlation between the geometry in the defect-free case and the behavior of the H could be found in this work. It seems that a strained bond favors the formation of an
H-E
center, however, H-E
centers also were observed for short bond distances in our calculations. A simple distinction
criterion, based on trap levels or on transition barriers to and from those states, unfortunately, cannot be deduced. Although, it will be shown in the following chapter that the strained bond criterion seems to be associated with more stable configurations, i.e. higher
barriers. To conclude: a defect forming at a strained bond seems to be more stable, and also more likely to form an H-E
center. However, the converse argument that an H-E
formed at non-elongated bonds automatically would be more stable than other defect
candidates, cannot be supported by the data.
As mentioned above, due to the amorphous nature of the structure it is very unlikely that any defect would find the right conditions to be able to act as a new three- or four-state defect in its new, volatile, location. Whether or not it will stay in this volatile state depends
on the barriers and also on the barrier
to the other charge state when volatile. Depending on the
barrier heights
and
the defect could however still capture and emit charge as a
simple two-state defect. If active, this would mean that this defect could potentially be detected in measurements when volatile. This is discussed in detail in Section 5.4.
Figure 5.6: Atomic configurations for three examples of H-E centers undergoing a volatility transition from state 2
to
. H atoms are shown as silver, Si atoms - yellow and O atoms - red. The turquoise bubble
represents the lowest unoccupied orbital for the positive charge states, the green bubbles represent the localized highest occupied orbitals for the neutral charge state. The main difference is the behavior in the neutral volatile state
that exists in three possible configurations (see also Fig. 5.5
bottom). The H can either stay attached to the O atom (top), break one of the bonds forming a new H-E
center (middle) or become interstitial (bottom). Beneath the figures, a schematic showing the
approximate position on the PES similar to Fig. 5.4 is given. Note that the volatility transition in the upper two cases ends at a neighboring O atom whereas for the bottom example it undergoes a cross-ring
hopping. The dependence of barrier height on this distinction is investigated in more detail in Section 6.2.
1 The negative-U character states that in thermal equilibrium the neutral charge state is never thermodynamically favorable, since the formation energy of the positive and negative charge states is always lower.
5.3 Volatility Barriers
|
Type |
|
|
|
|
|
HB positive |
3.24 |
0.56 |
6.22 |
3.48 |
|
Min |
2.64 |
0.16 |
20.72 |
2.70 |
|
HE’ neutral |
1.38 |
0.60 |
1.56 |
2.49 |
|
Min |
0.83 |
0.49 |
2.02 |
0.94 |
|
HE’ positive |
1.54 |
0.55 |
1.70 |
2.87 |
|
Min |
0.87 |
0.43 |
1.35 |
0.91 |
Figure 5.7: Histograms of the calculated barriers for H relocation (the barrier in Fig. 5.4),
for both the neutral and positive charge state. Note that for the HB neutral (top left) the depicted values are not
but rather just
in Fig. 5.4, as discussed in the text.
The two arrows indicate the expectation value and the expectation value of the minimal barriers (
). The latter is calculated from the minimum barrier found
for each of the specific initial configurations (depicted in red). Also, a fitted Weibull distribution (WBD) is sketched schematically. In the table, the expectation value and the characteristic parameters
(
for a Normal distribution or
and
for the shown WBD) are given. The reasons why the
barriers in the vicinity of 5 eV for the positive H-E
center were omitted from the statistical consideration are discussed in the text.
As can be seen in Fig. 5.4, the determining barrier for a defect to reach the volatile state is . In Fig. 5.7 histograms for these barriers calculated using the NEB algorithm are
depicted for different defect species. In these calculations, the relocation barriers to the 15 nearest neighbors for each defect were determined. The comparison comprises three HB and six H-E
center defects. As mentioned above, barriers lower than 1.0 eV would be desired to
be able to explain the volatility behavior as seen in the measurements. Such barriers could not be found for the HB. Note that for the neutral HB (top left) the depicted values are not
but rather just
in Fig. 5.4. Since
is per definition an infimum of the possible barrier
, these values are already sufficient to conclude that the HB
in its neutral charge state is a poor candidate for the suggested volatility mechanism. The actual value of
is expected to be much higher, but due to the high
computational costs of NEB calculations (see Section 4.3.1) their determination was disregarded.
For the positive charge state of the HB, the simple comparison of was not sufficient to discard this defect as a candidate for the H relocation mechanism.
However, most of the nearest neighbors the H
could relocate to already lie more
than 1.0 eV higher. Those were disregarded for the computationally costly NEB calculations, explaining the low number of calculated barriers in Fig. 5.7 top right. The remaining calculated
NEB-barriers were much too high and provide the conclusion that the HB is not suitable for the proposed mechanism. Note that in Fig. 5.7 there is a distinction between the expectation value and the
expectation value of the minimal barriers (
). The latter is calculated by averaging just the minimum
barrier found for each of the specific initial configurations (3 HB, 6 H-E
centers). Due to the exponential dependence of the transition time on the barrier height,
has to be considered as the actual determining property
for the volatility.
For the H-E center the expectation value is considerably lower. Note that for the positive charge state a
few barriers in the vicinity of 5 eV were found, which do not seem to belong to the distribution on the left-hand side. An energy so high would already be above the ionization energy in a Si-
band model as present if
is the oxide material in a Si-based transistor (see
Appendix A.4). Therefore, these values were omitted for the statistical considerations here. Furthermore, these high barriers do not contribute at all to the more important value for volatility,
. In both investigated charge states
lies at 0.83 eV (neutral) or 0.87 eV
(positive) at an ideal position for the suggested volatility mechanism. According to eq. (5.1) this corresponds to an expectation value of the volatility time constant at room temperature of
65 s for the neutral H-E
center or
5.6 min for the positive H-E
center. These expectation values are on the same order of magnitude as the measured time constants for volatility. In addition,
barrier heights corresponding to time constants of several minutes to hours at elevated temperatures would only be slightly higher. As can be seen, even lower barriers could be found in these structures. Unfortunately, even though
definitely is the most important parameter for volatility,
whether or not a defect would indeed be volatile (or detectable as such) in the measurements does not only depend on the barrier
. This more complicated interplay of four barriers will be
discussed in the following section.
The parameter distribution in Fig. 5.7 is clearly not symmetric. Therefore, an approximation using a normal distribution (ND) might not be very accurate. The expectation value is indicated by the arrows. In
the table in Fig. 5.7 the standard deviation for a ND is given. One additional problem with the ND
is that it would allow negative barrier heights to a certain extent, which is clearly unphysical. Therefore, an asymmetric probability distribution for only positive-valued random variables was fit to the data. For this purpose the Weibull-distribution [186] (WBD) was chosen
(see Appendix B). This is an obvious choice since the present problem fits the weakest link problem [187, 188]. The characteristic of this
distribution is determined by the shape parameter
and the scale parameter
(see Fig. B.1 and table at Fig. 5.7). The expectation value is the same as for the ND (since it was fitted to the same data). However, note that due to the asymmetry
the peak value is in general not the expectation value. Using this distribution it is possible to estimate the probability for defects to show volatility behavior. We previously defined that the barriers
should be lower than
1.0 eV to be able to measure volatility at room temperature. According to the fitted
distribution a minimal barrier lower than this should be found for
68% for both the neutral and the positive H-E
center (a combined probability2 of
90% to find such a low volatility barrier in at least one of the charge states of a four-state
defect). However, one has to consider the observation window of a single measurement. At room temperature, for example, a probable detection window should have volatility time constants in the range between several minutes to one day. According to eq. (5.1), this dramatically reduces the window to a range between
0.83 and 1.0 eV. This would still hold true for
14% of the neutral and
9% of the positive H-E
center defects (a combined probability of
22% to find a defect showing volatility in the specified window).
|
|
Neutral [eV] | Positive [eV] | ||||||||
|
Type |
|
|
|
|
|
|
|
|
||
|
Stick |
2.02 |
0.46 |
1.08 |
0.41 |
1.38 |
0.67 |
1.26 |
0.72 |
||
|
Break |
1.46 |
0.50 |
0.84 |
0.62 |
1.64 |
0.52 |
1.55 |
0.55 |
||
|
Interstitial |
1.03 |
0.28 |
0.47 |
0.20 |
1.47 |
0.37 |
1.34 |
0.35 |
||
Figure 5.8: Correlation plot for the forward () and reverse barriers (
) of the volatility transition for both the neutral and positive
charge states (see Fig. 5.4). The possible observation window for volatility is indicated by the blue area. Note that the defects in this chart are all grouped by their behavior in the neutral charge state (see Fig. 5.5 bottom), since H
always tends to stick to a bridging O atom3.
The respective mean value for each group is indicated by the horizontal and vertical lines, the mean values and standard deviation are given in the table. The more complex interplay of all four barriers that have to be considered in the volatile states is discussed in the
subsequent Fig. 5.9.
Therefore, we can conclude that the H-E center is a promising candidate for explaining volatility within the suggested H relocation
mechanism, whereas the HB is not. We will thus focus only on the H-E
center in the following considerations. As mentioned above, there are three possibilities to
relax into the neutral state
, referred to as
(see Fig. 5.5 bottom and Fig. 5.6). The H
can either become interstitial, break one of the bonds of the bridging O atom (resembling
state
in Fig. 4.1 H-E
, or just stay attached. The first case is of considerable importance since it could also provide an explanation for defects disappearing completely during the measurements if the interstitial H
diffuses away. The last case, where the H stays attached to the bridging O atom is only
possible if the H
can donate its electron to an electron-accepting site nearby. This could be, for example, a Si
with a wide O–Si–O bond angle [157]. It is therefore important to determine whether the lower barriers are associated with one of the different types.
For the lowest barriers of each set, there is no clear favorable transition. Three are associated with interstitial H, two with H-E
centers and one with the ”stick”-configuration. Note, however, that the latter one is found in a
structure where this behavior is dominant and therefore most likely overrepresented in this study, as discussed above. A closer examination for the whole set of barriers of Fig. 5.7 can be carried out using correlation plots as in Fig. 5.8. These plots show the correlation between the forward (
) and reverse barriers (
) for volatility (see Fig. 5.4). The possible assumed observation window for volatility is indicated by the light blue area. For this window we assume a volatility time constant of 1 min at room temperature as a lower boundary and of
1 month at 350 °C as an upper boundary. According to eq. (5.1) this corresponds to barrier values of 0.83 eV to 2.27 eV, which is a very generous estimate.
The correlation for the neutral and positive charge state are very different. For the neutral charge state, the values are located under the main diagonal, indicating that the "active" state lies lower in energy than the volatile state. Furthermore, most defects lie outside the
observation window. Of particular interest are the barriers and
for the transitions to and from a neutral interstitial state
since they could be responsible for a defect to disappear entirely when the H diffuses away. There are a few defects where
is so low that it would already be overcome at room
temperature and therefore the respective defects would be unstable. There are, however, also defects where the barrier is in the right range around 1 eV to explain measurement observations. Note that for interstitial H
the barrier
back to the bound state is on average 0.47 eV
and therefore a defect having lost its H atom could easily capture one again, if an interstitial H
passes by. It will be shown that this correlation between forward and reverse barrier also
holds true for more generic H hopping transitions discussed in Chapter 6.
The correlation of the barriers is completely different for the positive charge state. Here the volatile states are nearly isoenergetic when compared to the "active" states, partly even lower, as already reported in [YWC5]. Also, most of the states lie within the observation
window indicating that the suggested volatility mechanism would preferably occur (and be observable) in the positive charge state. For both charge states, there are several points at the very bottom of the chart indicating a very low barrier . These states are very unstable and would consequently
relax back quickly into their initial state. Thus, they would also not be observable in our measurements. Values higher than 5 eV were not included in the statistics since an energy so high would already be above the ionization energy in a Si-
band model as present if
was the oxide material in a Si-based transistor (see
Appendix A.4).
For the neutral charge state the transitions leading to states where the H sticks without breaking a bond seem to be on average higher, the reason for that is unknown. They would, however, be the only type which shows mean values clearly within the observation window (indicated by the crossing of the green lines). For the other groups discussed in Fig. 5.8, no clear tendency can be deduced,
although one should note that the sample is rather small. Since there are no distinct clusters visible in Fig. 5.8, it is not possible to deduce the preferred behavior of a defect in the neutral volatile state
by the barriers and
or vice versa. These two barriers govern whether a defect
reaches the volatile state and is able to stay there. However, note that in the volatile state the defect should theoretically also be able to change its charge state, which involves an NMP-transition. This possibility and its implication for the measurement is discussed in the
following section.
2 This probability is given by the reverse probability of not finding volatility at all for both cases.
3 It should be clarified that H does not stick to every bridging O atom. For
0.7% it was observed that during geometrical optimization the H
moved to a neighboring bridging O, where it would attach to. So in the end H
always tends stick to one bridging oxygen, in more than 99% the one it is placed next to in DFT
calculations (see also Section 6.1).
5.4 Would Volatile Defects be Visible in Measurements?
Since the HB was already discarded as a possible candidate for the suggested volatility mechanism, only results for the H-E center will be discussed in this section. Up to now we have only discussed the
transitions
or
. However, reaction barriers between the states
and
(see Fig. 5.4) are also of great interest
for determining whether the defect would possibly be electrically active when volatile and therefore possibly visible in RTN or TDDS measurement (see Section 1.2). When volatile, the dynamics of the
defect are determined by the barriers
and
between the states
and
(
and
for the neutral volatility transition) and by the barriers between the states
and
(
and
), as can be seen in Fig. 5.4 and Fig. 5.8.
and
can be calculated using the CI-NEB method, as described
in the previous section.
and
can be determined in the classical limit of NMP theory (see
Section 2.2.1) by the intersection point of their potential energy surfaces. Note that the definition of
and
is chosen in a way that they are always assigned to the
respective forward and reverse barrier of the transition (see Fig. 5.4). This means that for defects becoming volatile in the positive charge state
refers to a transition from positive to neutral, but vice versa
for defects that become volatile when neutrally charged.
The correlation plots in Fig. 5.9 summarize the complex interplay of the four barriers mentioned above. In this figure, the size of the points indicates the possibility for a certain volatile state to be reached in the first
instance. If the barrier is high the possibility to reach the state is small (small
point) and vice versa for small
. When in the volatile state, one then has to distinguish
between two cases: If the barrier
between the states
and
is higher than the barrier
back to the active region (see Fig. 5.4), or has at least the same height, this would leave the defect electrically inactive in the measurements (grey part in Fig. 5.9 top). Any charge capture or emission
event in state
would occur with a similar or lower frequency as volatility itself.
Figure 5.9: Correlation plot for the barriers ,
and
discussing whether or not a defect would in principle be
electrically active in the volatile states. The definitions of the barriers are given in Fig. 5.4. Additionally, the probability to reach the volatile state in the first instance (the barrier height
) is indicated by the size of the points (small
unlikely, large
likely). The barriers are shown for three different shifts (as imposed by an electric field).
Top: If
is larger than
, the defect is of course preferably inactive. If not, in prin-
ciple the defect could act as a two-state defect when volatile. The blue and gray area’s limits form the possible observation window, as discussed in the text, limited by the maximum and minimum observation time of those effects.
Bottom: For RTN observations rather similar
and
are required. This is not the case for the vast majority of the
defects, moving them far outside of the RTN detection window. However, as discussed in the text, those defects should be visible in TDDS, but the signal would most probably not be identified as being related to the initial defect.
The second case occurs if the barrier is indeed lower than
(blue part in Fig. 5.9 top). Such a defect could be electrically active in the volatile state as well. However, note that the vast majority of the points in this region are very small, indicating that the possibility to reach this volatile state in the first place is very low (high
). Furthermore, for all the calculated defects the
barriers
and
are found to be of very different height. Typically
for the defects overcoming the volatility barrier in the
positive state and vice versa for the ones making the volatility transition in the neutral charge state (see Fig. 5.4 bottom). Therefore, the defect could indeed be electrically active, but at the same time hardly
observable in RTN measurements due to its very short dwelling time in the energetically higher state [3]. For the observable RTN measurement window in Fig. 5.9 bottom, we assumed a maximum ratio of capture and emission times by a defect of 100 and a minimum such ratio of 0.01. The window is further limited by minimum time constants of 1 ms at room
temperature and a maximum of 1 ks at 350 °C. According to eq. (5.1) this corresponds to barrier values of 0.56 eV to 1.87 eV, which is a very generous estimate. It must be
kept in mind that in TDDS, due to different emission times, this kind of defect would theoretically be visible, but as a different cluster to the initial defect in the spectral map (Fig. 1.2). However, due to the different
emission times, this new cluster would show up on the maps with a similar step height but at a different time. Therefore, it would most probably not be associated with the original defect in such a spectral map.
The limits of the blue and gray area in Fig. 5.9 (top) indicate the possible assumed observation window for volatility. For this window we assume a volatility time constant of 1 min at room temperature as a
lower boundary and of 1 month at 350 °C as an upper boundary. According to eq. (5.1) this corresponds to barrier values of 0.83 eV to 2.27 eV, which, again, is a very generous
estimate. Nevertheless, only very few of the neutral defects lie within the window, because of their small barriers , as already observed in Fig. 5.8.
When an electric field is applied, the PESs in Fig. 5.4 shift relative to each other, thereby changing the barrier heights. In Fig. 5.9 this results in the points
shifting parallel to the x-axis (top) or perpendicular to the diagonal (bottom). Obviously, defects becoming volatile in the neutral states move in the opposite direction compared to those which become
volatile in the positive state. It should again be noted that the barriers and
are (to first order) unaffected by the electric field (see
also Fig. 5.4 and Chapter 3.1). Therefore, in this model volatility is a purely thermally activated process. This can also be seen in Fig. 5.9 (top) where a different electrical shift
does change the value of
but neither of
(the corresponding points only move parallel to the
x-axis) nor of
(the point size of the corresponding points is
constant).
5.5 Conclusions
The proposed expansion of the NBTI four-state model including possible H relocation is able to explain the observed volatility in experiments, given that the responsible defect is the H-E center. The HB, on the other hand, is not a suitable candidate to explain volatility behavior
with the suggested mechanism. Barriers for the HB are much too high to be able to explain the experimental observations. From the calculations of the barriers to the nearest neighbors several conclusions can be drawn:
-
• In the positive charge state the H
always sticks to a bridging O atom.
-
• In the neutral charge state there are three possible ways for the H
to behave, one of them being the H
becoming interstitial. This is especially interesting since an interstitial H
could diffuse away after such a transition, giving a possible explanation for defects disappearing entirely from the measurements, also providing a viable mechanism for H release under weak bias conditions. H
, on the other hand, could also be imagined to gradually drift away when “hopping” between the bridging O atoms. These transitions will be subject of the investigations in the following chapter.
-
• The volatility transition can occur in both charge states, however, the reverse barriers indicate that the volatile states would be more stable in the positive charge state. The mean value of the determining barriers (
) lies where it is expected due to experimental results.
-
• A considerable amount of the defects could theoretically be electrically active when volatile. However, it could be shown that due to the interplay of the involved barriers those defects would hardly ever be observable in RTN measurements. Even though such a defect should be visible in TDDS, it would have different emission times and, therefore, would most probably not be associated with the original defect.
As already mentioned in Section 4.4, it should be kept in mind that the current modeling approach does not consider any
possible dependence of the thermal transition barriers on the electric field and that this dependence should be subject to further investigations. The proposed mechanism of H relocation should, however, not be exclusively possible for defect sites. Such a
"hydrogen hopping" process could in principle be possible between any two bridging O atoms the H can bind to. A closer investigation of this hopping mechanism is important to better understand H kinetics in a-. This will be discussed in the following chapter.
6 “Hydrogen Hopping” Transitions
DFT calculations show that in amorphous (a-
) protons (H
) can be trapped in various configurations [YWJ2, 159, 179, 189, 190]. In the previous chapter, it
was shown that the hydrogen (H) relocation from a hydroxyl-E
center (H-E
center) to a neighboring oxygen (O) atom is in principle capable of explaining the volatility
observed in measurements. The concentration of H in the oxide material (the literature provides values of
1018 to 1019/cm3 [191–195]) is on the same order
of magnitude as the experimentally observed defect density (see Section 1.1.1)1 , which corresponds to only a handful of defects in
modern devices [36, 51, 196, 197]. Therefore, it is of high interest to investigate H dynamics in greater detail. An H hopping mechanism for explaining H
movement through a-
is used throughout the literature [164, 198–202].
However, the experimental results on the activation energy as well as the theoretical calculation of this barrier are very controversial as can be seen in Tab. 6.1. Furthermore, note that all the
publications in Tab. 6.1 only consider H
hopping.
For the neutral hydrogen (H) such a hopping process has not been reported in the literature until now. Publications only
focus on the activation energy for H
migration between
voids [143, 203–205], which is quite consistently reported in all of those works at around 0.2 eV. However, note that this is not the barrier that would be associated with a hopping process between bound states, such as that of H
hopping. Unfortunately,
there are also hardly any theoretical calculations dealing with H
hopping barriers in
present in literature. This is mainly due to the fact that
H
is often not considered stable in
because of its negative-U character [184, 185,
206]. However, as has been shown previously in this work, DFT calculations indicate that H
can be stable in a-
. It has to be noted that the negative-U property
is determined for a thermal equilibrium and therefore it does not hold information about any possible metastable neutral configurations of H.
| Method |
|
Publication |
| Experimental |
0.82 ; 0.87 |
[207] |
| Experimental |
0.81 |
[208] |
| Experimental |
0.6 ; 0.7 |
[209] |
| Experimental |
0.38 |
[210] |
| DFT (LDA) |
|
[211] |
| DFT (LDA) |
0.73 |
[202] |
| DFT (GGA) |
1.15 |
[202] |
| DFT (PBE0-TC-LRC) |
0.66 |
[79] |
| Hartree-Fock |
0.87 |
[201] |
| MD (GGA) |
0.50 |
[200] |
| MD (ReaxFF[212]) |
0.05 ; 0.33 |
[199] |
Table 6.1: Values for H hopping in
found in the literature. There is a large discrepancy be-
tween the different values, experimentally as well as theoretically calculated. In parenthesis the used functional (see Section 2.1) is stated if required for the method. It seems clear that values calculated by molecular dynamics (MD)
simulations are lower than for DFT since in MD the host structure can vibrate. However, a value of 0.05 eV as stated in [199] seems peculiar. Unfortunately, publications treating the neutral counterpart of this reaction are very rare and only focus on the migration barrier between voids [143, 203, 204], therefore no such chart can be presented for H
hopping.
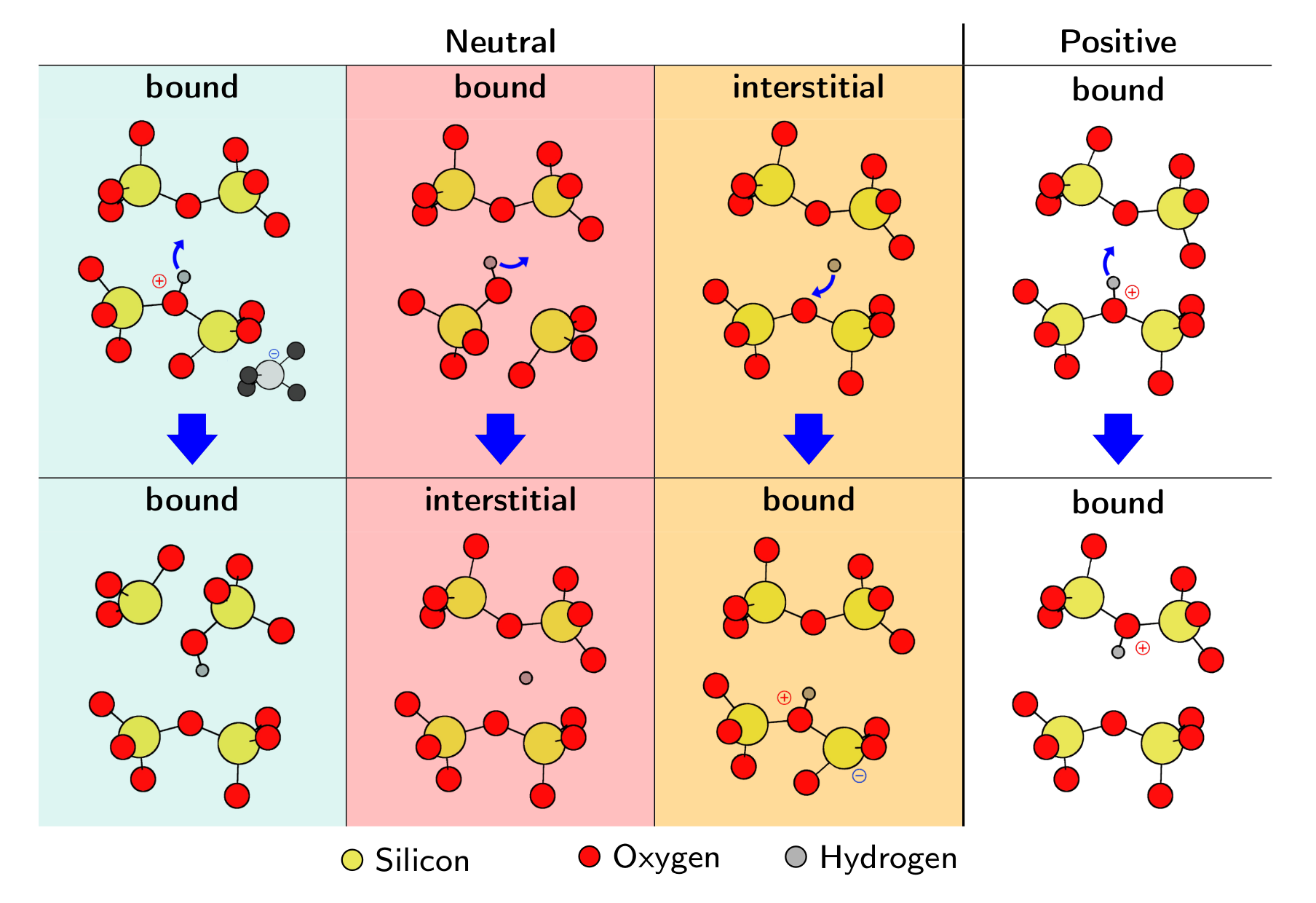
Figure 6.1: The transitions considered for the H hopping. As already shown in Fig. 5.5, an
H always tends to bind to the bridging O atom. In Fig. 5.5
three possible neutral configurations are discussed. However, for the H hopping it is only of interest whether the H
is bound or not. Thus, in this chapter we only distinguish between bound and interstitial H.
Therefore, the configurations which were called “stick” and “break” in Chapter 5 are summarized as “bound” in this chapter. Note that the depicted neutral transitions above are just examples.
For the permanent component of NBTI degradation, a gate-sided H release model was recently proposed by Grasser et al. [YWC1, YWC3], based on hydrogen hopping
transitions (see Section 3.2). In this chapter the hopping barriers for H in a- are investigated in more detail. Thus, barriers to hop
from one bridging O atom to the next one will be considered in the neutral and in the positive state. Again the neutral state shows more variety than its positive counterpart. It will be shown that the mechanism
for H transport is very likely more complex than suggested by the H release model. The dependence of the hopping barriers on the different ring sizes in a-
is also discussed. Moreover, it will be investigated
whether barriers are different when hopping between neighboring atoms of the ring, or rather “cross-ring”. Finally, an attempt to reformulate the NBTI four-state model by using only H hopping transitions is discussed. This attempt, however, will be shown to be an
impasse.
6.1 Barriers for Hydrogen Hopping in a-SiO
Similar to the barriers in Fig. 5.7, barriers for H hopping were calculated to obtain reliable statistics of the barrier heights for these transitions. Therefore, in two of the defect-free 216 atom a- structures created as described in Chapter 4, H was placed next to each of the 144 O atoms at a distance of 0.7 Å. The created structures then underwent geometry optimizations in their positive charge state. With just very few exceptions where
the H moved to a neighboring O, the H stayed at the O where it was placed next to. In all cases the H
ended up attached to an O atom. Subsequently, the resulting configurations also underwent geometry optimization in the neutral charge state. As a result of this optimization 41% of the H
became interstitial and 59% stayed attached to the O atom in the neutral charge state.
In Chapter 5 three different configurations in the neutral charge state were considered (see Fig. 5.5). Results from this section reveal that the definition of the “stick” state due to a bond distance criterion (deduced from [YWJ2]), as in the previous chapter, might be problematic. When a Mulliken charge analysis [182] is carried out to
determine the relative charge of the atoms in the structure, typically a positive charge located at the H atom and a negative charge at one of the Si atoms is found. The calculations carried out in this section revealed that occasionally also for Si–O distances 2.0 Å the negative charge sits at one of the two Si
atoms associated with the defect, resulting in an overall neutral defect. Electronically this resembles more an H-E
center. In subsequent works, it should, therefore, be investigated if a distinction by Mulliken
charge analysis would be a better criterion. In any case, the more problematic defects are those “stick”-configurations which give their electron to a Si atom further away, since this could lead to a
violation of the adiabatic approximation (and therefore a much lower possibility to occur, see also Section 5.2 and [183]). However, even if this fraction had to be disregarded, the order of magnitude of the
defect concentration would not change considerably. Only
10% of all defects (
16% of the “bound” configurations, see below) were found to be of this type. Note that
in Fig. 6.1 both these possibilities are sketched.
Fortunately, for the H hopping, which will be investigated in more detail in this chapter, it is only of interest whether the H is attached to a bridging O (bound) or not (interstitial). This leaves three
transitions that have to be considered: boundbound, bound
interstitial and interstitial
bound, as can be seen in Fig. 6.1. It should be emphasized again that no correlation between the trap level of the defect and the behavior of the H
according to Fig. 5.5 could be found
in this work (see also Section 5.2). It seems that a strained bond criterion produces more stable defect configurations and furthermore favors the formation of an H-E
center. However, the converse argument, that every H-E
center automatically would be more stable than other defect configurations must be rejected
since it is not supported by the data.
Similar to the previous chapter, the ten configurations lowest in energy were chosen (five in the neutral charge state) and NEB-calculations to determine the H hopping barriers to their ten nearest
neighbors were carried out. Since this was done for two different a- clusters, this leads to a sample of twenty initial
configurations (ten in the neutral charge state) and barriers to the ten nearest neighbors for each of them. If, however, the energy difference between the initial and final states was already larger than 1.5 eV this nearest neighbor was disregarded, and instead
another neighbor was added to the list to obtain ten barriers for each initial configuration. Unfortunately, the NEB algorithm is known to not converge properly when the initial path is badly chosen (e.g. when in one image the atomic distance is unphysically low [213]). However, this cannot explain the relatively large
number of NEB calculations which did not converge properly (approximately a fourth in the positive charge state, and nearly half in the neutral charge state). It is suspected that many of the selected
paths are just unsuitable for a proper transition and therefore did not converge. Also, the turnout of the neutral NEBs could have been improved when running the non-converged calculations considerably longer. This, however, was not done due to the enormous amount of
additional core hours needed, while not significantly improving the statistics.
|
Type |
|
|
|
|
|
bound |
1.47 |
0.61 |
2.59 |
1.64 |
|
bound |
1.79 |
0.49 |
4.24 |
1.97 |
|
interstitial |
0.60 |
0.74 |
- |
- |
Figure 6.2: The three different types of hopping barriers in the neutral charge state. Barrier energies larger than 5 eV were disregarded due to reasons discussed in the text. The vertical arrows
represent the mean values. A fit to a Weibull distribution (WBD) is presented. In the table, the expectation value and the characteristic parameters of each distribution are given. We see that expectation values are lower for the boundbound transition than for bound
interstitial. The right panel depicts reverse barriers of the middle panel, thus the intersti-
tial
bound transition.
First, let us consider only the neutral charge state. The barriers for the three different paths as described in Fig. 6.1 are shown in Fig. 6.2. In this plot values higher than 5 eV are again neglected since this would already be the ionization energy in a Si- band model. The expectation values and a fit to a
Weibull-distribution are depicted. It is clearly visible that the barriers to an interstitial state are on average higher than the bound
bound transition associated with “hopping”. Maybe even more noticeable are the
barriers for the transition interstitial
bound (right panel). This barrier is of utmost importance to conclude how interstitial
H
would behave in a-
. The barriers for the H to bind to the O are partly even
lower (about half of the barriers are lower than 0.15 eV) than the diffusion barriers calculated for H
in
[205]. Given the high diffusivity of H in
[143, 203–205] and the very low barriers found for this
reaction, one can conclude that the H would not diffuse far but attach to one of the next bridging O. Therefore, at low temperatures the diffusion barriers between the multiple voids in a-
could become the dominating factor for this reaction,
explaining the vanishing H
signal observed in [143] at
100 K.
Consider that binding in the neutral state seems to be possible for 59% of the O atoms in the investigated a-
structures and about half of those have such low
H
capture barriers. This leads to the conclusion that in the neutral charge state, H kinetics in
a-
would resemble more an H hopping process in which only the O atoms H
binds to can participate in. Consequently, as a simplification, the barriers for
bound
bound and bound
interstitial will be combined and just treated as the neutral hopping barriers in the
following.
|
Type |
|
|
|
|
|
Neutral |
1.54 |
0.60 |
2.81 |
1.72 |
|
Min |
0.68 |
0.54 |
1.39 |
0.75 |
|
Positive |
1.38 |
0.72 |
1.93 |
1.54 |
|
Min |
0.45 |
0.30 |
1.50 |
0.49 |
Figure 6.3: Histograms for the calculated barriers for H hopping, for both the neutral and positive charge state. The two arrows indicate the expectation value and the expectation value of the minimal barriers.
The latter is defined as the expectation value of the minimum barrier found for each of the specific initial configurations (depicted in red). The values of 0.68 eV (neutral) or 0.45 eV (positive) are rather low and could therefore easily be overcome by thermal
excitation already at room temperature. Thus, it can be assumed that H is constantly hopping through the material in accordance with the model suggested in Section 3.2. A normal distribution
(ND) fitting these histograms would allow for negative barrier values, therefore a fitted Weibull-distribution (WBD) is shown. In the table, the expectation value and the characteristic parameter ( for the ND or
and
for the WBD) for each distribution are given. The rea-
sons why the barriers in the vicinity of 5 eV for the neutral charge state were omitted from the statistical consideration are discussed in the text.
The results of the unified neutral barriers (boundbound and bound
interstitial) and also the positive hopping barriers are shown in Fig. 6.3. Similar to Fig. 5.7 the two arrows indicate the expectation value and the expectation value of the minimal barriers (
). Note that for the neutral charge state, again, a few
barriers in the vicinity of 5 eV were found, which do not seem to belong to the distribution on the left-hand side. Also here these values were omitted out of statistical considerations. The mean value of the calculated barriers is clearly much too high to explain the
experimentally observed behavior. Since the H atom will preferably choose the lowest of the possible barriers when hopping away from its current position the minimum barriers are the determining factor for the H hopping transitions.
The important value is again , the expectation value of the minimum barriers found for
each of the specific initial configurations (ten structures in the neutral charge state and twenty in the positive charge state). It was calculated to 0.68 eV (neutral) or 0.45 eV (positive). Similar to Fig. 5.7 a fit using the Weibull-distribution (WBD) is depicted (see also Appendix B). The characteristic parameters (
for the ND or
and
for the WBD) for each distribution are given in the table.
The expectation values for the barrier energies are rather low and can easily be overcome by thermal excitation already at room temperature. It can thus be assumed that H is constantly hopping through the material in accordance with the H release model (see Section 3.2). H
was found to stick to nearly all O atoms in the structure, H
to
59%, which should lead to a higher mobility for the H
when detached. On the other hand, the barrier to detach H is higher in the neutral state.
Furthermore, as shown above, an interstitial H
would not be able to diffuse far in a-
, because of the extremely low capture barriers of about a
third of the bridging O atoms.
The only difference between the H hopping transitions and the volatility transitions for an H-E center discussed in the previous chapter, is the initial state. Whereas a hopping transition can
start from any O in the structure (note that in the statistics above, the states with the lowest total energy of the structure were used), the starting point for a volatility transition is an H-E
center having a highly strained bond (see Section 4.2.3). Comparing these results with the volatility barriers obtained from the H-E
center in Fig. 5.7, one can see that
the H hopping barriers are considerably lower. This links the H hopping with the four-state NMP model for NBTI (extended by volatility) as described in the previous Chapter 5. In an a-
where H is present, the H atoms would move through
the oxide of a MOSFET transistor by hopping transitions, showing temperature and, for H
, bias dependence. If the H
eventually reaches the defect site by hopping transitions it will inevitably form a defect. The frequency of this defect formation would hence depend on temperature, bias and H supply and remains to be investigated by a hydrogen hopping model derived from the above
assumptions. A challenge for the implementation of such a model will be how to model two atomic hydrogen meeting in the oxide. It is suspected that this would lead to the formation of H
. Furthermore, as seen in the following section for the
interaction of multiple H atoms at defect sites, the process might even involve three H atoms. Nevertheless, the resulting model would likely predict a large buildup of H
in the oxide. Thus, a complete model should include a viable
H
cracking mechanism in order to keep balanced
concentrations, this mechanism also remains to be clarified.
6.2 Ring Size and Cross-Ring Hopping
Figure 6.4: A ten-member ring in , in which the H
undergoes either a neighbor hopping or cross-ring hopping transition. The cross-ring hopping is
typically associated with lower barriers [79, 200] (see Fig. 6.5).
An -quartz structure of
only consists of twelve- and sixteen-member rings. The
ring size
is the number of atoms forming the ring, so for our
structures the number of oxygen (O) and silicon (Si)
atoms forming a ring of ring size
is always
. In an amorphous structure, a greater variety of rings exist.
It has been shown in previous works that barriers for H
hopping are lower when the H
does not hop to a neighboring O atom but rather to another O across the ring [79, 200] (see
Fig. 6.4). Therefore, the barrier data calculated in the previous section was analyzed to see whether the hopping procedure is onto neighboring atoms or cross-ring. For the following analysis cross-ring
hopping was defined as follows:
-
• Hopping onto the next O atom of a ring is never cross-ring.
-
• Hopping onto the second O in the ring is only considered as cross-ring if the distance of the involved O atoms is larger than 4 Å.
-
• All other hopping transitions are considered as cross-ring.
Figure 6.5: Comparison of calculated barriers for H hopping based on whether or not they belong to a cross-ring hopping transition. The data is grouped by the ring size of the ring where the transition takes place. By definition
(see text) there is no cross-ring transition at a ring size of six. However, it can be seen that for the neutral charge state cross-ring hopping does not seem favorable for small rings since no data is present in the graph above. The underlying data is shown transparently in the
background, indicating that there is no correlation between the behavior in the neutral charge state (whether H is bound or interstitial) and the hopping characteristic or ring sizes.
Thus, applying the above definition, for cross-ring hopping at least four O atoms have to be present in the ...-Si-O-Si-O-... ring, so there is no cross-ring hopping up to a ring size of eight. The second criterion was introduced in order to limit the definition of cross-ring hopping for larger rings where the geometry seems unfavorable and resembles much more a neighboring transition than cross-ring.
For this analysis, the (defect-free) structures were analyzed using the RINGS code [214] with the King’s shortest path criterion [215, 216]. Thereby, ring sizes from 6 to 18 were found in our structures. Of course, a set of two O atoms can potentially be found in more
than one ring, especially if they are a part of a large ring. If so, the smallest ring containing this combination was chosen. The resulting comparison is shown in Fig. 6.5. Note that this figure comprises the same
data set as Fig. 6.3 but the calculated barriers for H hopping are depicted based on whether or not they belong to a cross-ring hopping transition. Furthermore, the data is grouped by the ring size where
this transition takes place. It can be seen that for the neutral charge state, cross-ring hopping does not seem favorable for small rings since the analysis did not show any contribution in this area. There is no correlation between the behavior in the neutral charge state
(underlying data is shown transparently in Fig. 6.5) and the hopping characteristic or ring sizes. However, it is clearly visible that the barrier for cross-ring hopping (pink) is on average lower than when
hopping to neighboring O atoms. This has been already reported for H in [79, 200]. Here it is shown that this also holds true for neutral H. The reason why also the H
interstitial transitions are included into these statistics were discussed above in the
previous section. Note that there is considerably more underlying data for the neighboring transitions. This originates in the initial selection criterion for the transitions, which focused on the nearest O atoms
around one initial configuration. This naturally favors next neighbors. The dataset comprises sets of the barriers to the ten nearest neighbors of several initial states (see above).
6.3 Implications for the H Release Model
The hopping transition barriers for H and H
calculated in this chapter turn out to be on average at a comparable height. For a model as
described in Section 3.2, this means that hopping in both charge states seems possible. The mobility could suspected to be
slightly higher in the neutral charge state (since H
only binds to about 59% of the O atoms), however, barriers are lower for the
H
hopping. Furthermore, similar to the volatility transitions there is the possibility to switch the
charge state at every location and the possible external driving force of an electric field that has to be considered, leading to a complex interplay of many factors.
The H release model suggested in [YWC1, YWC3] does not consider an H contribution to H transport in a-
. This is due to the assumption that interstitial H
is very mobile and could diffuse very quickly over comparably long distances. Given the
above findings this has to be questioned for three reasons:
-
• The reverse barrier for interstitial H
to re-bind to a bridging O is found to be lower than 0.15 eV for about a third of the calculated sites. This is lower than the assumed diffusion barriers between the voids in a-
[205]. Hence, it must be assumed that the average lifetime of an interstitial H
in the a-
network would be very short.
-
• H
can also hop through the oxide without becoming interstitial. However, not every O atom can participate in this mechanism since it was found that H
only can bind to
59% of the O atoms in our a-
structures. Since we just concluded that interstitial H
is not assumed to diffuse very efficiently, this reaction has to be considered for an H release model too.
-
• The accountable barriers for H hopping in the neutral and positive case are on average nearly of the same height. Given the considerations above, the hopping of H
cannot be neglected for a proper formulation of such a model.
Moreover, the barriers calculated in this thesis are considerably lower than the barriers assumed in the initial formulation of the H release model in [YWC1, YWC3]. One should, therefore, refrain
from the assumption that H exchange can only take place via the H interstitial state as suggested by Fig. 3.6. On the other hand, the findings should reduce the diffusivity of interstitial H assumed in the model.
In the H release model (see Section 3.2), the limiting factor for H dynamics is the H release barrier rather than the transport
process in the oxide (see Fig. 3.5 and 3.6). This is in good agreement with the findings in this chapter since the on average low barriers found for H hopping
would determine the H exchange, whereas the bridging O atoms with higher hopping barriers can act as H release and trapping sites within the oxide. However, the results also show that the H release mechanism over a high barrier is not necessarily limited to a reservoir at
the gate of the device. Even higher H hopping barriers at the tail of the calculated distributions could in principle provide these release barriers 1.5 eV, given that H is initially bound at these
sites.
These findings also indicate the following important conclusion: Consider an a- structure with a precursor providing the basic features
needed for an NBTI four-state H-E
center (an elongated bond and the possibility to pucker as described in Section 4.2.3). If H is present to a certain amount, the H eventually reaches the defect site by hopping transitions after some time, inevitably forming such a defect. Furthermore, note that only
7% of the elongated bonds have the possibility to act as a four-state defect [YWJ1].
However, we can assume that the H release barrier for elongated bonds is the same, regardless of its ability to act as a four-state defect or not. Thus, the release barriers from such a site are the volatility barriers calculated in the previous chapter (see Fig. 5.7). These barriers have been found to be considerably higher than the average H hopping barriers, making these strained bonds suitable candidates for the H release and trapping sites in Fig. 3.6.
6.4 Implications for the Volatility Model
Figure 6.6: A possible explanation for NBTI-volatility alternative to the mechanism described in Chapter 5. The shown model is derived from barriers calculated in [YWJ2] and the hopping barriers discussed in this chapter, but only for the neutral charge state since no data has been calculated yet for the respective positive counterpart.
The findings in this chapter indicate that atomic hydrogen is able to move through the a- material by hopping between bridging oxygen atoms.
However, this also means that eventually atomic hydrogen could make its way to a defect site and interact with the defect. In [YWJ2] barriers for the interaction of interstitial H
and the H-E
center or the HB were investigated. A possible reaction path for those two defects is
presented in Fig. 6.6. Note that an interstitial H
would immediately passivate the dangling bond on either of the defect candidates making it
electrically inactive, since the DFT calculations indicate that this reaction is barrier-free. When a third H
passes by, there is a very low barrier for it to “pick” the second hydrogen from the defect site,
to form H
. This H
molecule, being very stable in the a-
environment, would then just diffuse away, leaving the
initial defect configuration. Note that the direct break-off of H
from the configurations in Fig. 6.6 (middle) is not favorable due to very high barriers. Also, the respective reverse reaction (precursor + H
passivated defect) showed much too high barriers to be considered in such a model
[YWJ2].
The rather low H hopping barriers in combination with the low barriers within this alternative model indicate that if H is present in the oxide, it would very probably reach the defect site by hopping
transitions after some time, triggering the reactions in Fig. 6.6. As already discussed above, the determining barrier for such a volatility reaction would neither be the hopping barriers nor the barriers
indicated in Fig. 6.6, but rather the barrier for H to be released into the oxide in the first place (see Section 6.3).
It should be noted that [179] and Fig. 6.6 only discuss the H reaction. A calculation for the positively charged HB in
-quartz Si showed that the “H-pick-up” in Fig. 6.6 (right) has a barrier of
1.5 eV, which would be too high for a proper
volatility reaction. This is not surprising since the H is expected to bind much stronger to the positively charged defect. However, as shown in the previous chapters, the situation can be very distinct in a-
, which is why in a subsequent work the positively
charged counterparts of the reaction in Fig. 6.6 should be investigated.
6.5 Alternative NBTI Four-State Model Using Hydrogen Hopping Transitions?
Figure 6.7: A possible alternative embodiment of the NBTI four-state model explained in Section 3.1 using only H hopping transitions. The important difference
to the previously suggested model is that here no puckering is needed to construct the states and
. The H hopping transitions have taken over the role of the puckering transition.
Due to the findings in the previous chapter, the question arises if a four-state model, as described in Section 3.1, could be constructed by only using H hopping transitions. Such an alternative formulation is
shown in Fig. 6.7 where the H sits at different O sites in states and
than in the states
and
. This different embodiment of the four-state model would possibly be able to solve the problem of the
barrier
being on average too small in the statistics carried out in Chapter 4 (see Fig. 4.4). For a model as depicted in Fig. 6.7, the assumption of puckering
transitions is not needed. Instead, the thermally activated transitions are assumed to be H hopping transitions as described in the previous section. Consequently, the mean value of the transitions
would be approximately 0.45 eV or 0.68 eV for the
transition
respectively. This would be in better accordance with the experimental
values in Fig. 4.4, and would also have a considerable impact on the
theoretically predicted defect concentration.
For the puckering four-state H-E, a strained bond (
1.65 Å) is needed, which additionally satisfies
the possible preconditions for a puckered state. The strained-bond criterion is fulfilled for
2% of the bonds, of which only
7% have the preconditions for a stable puckered state [YWJ1]. So approximately one in 700
O atoms meets both these criteria, which corresponds to a concentration of
6.23 × 1019 /cm3 or
1000 possible locations in the oxide of a
100 nm
100 nm
2 nm device. For the suggested
alternative this value would be much larger since only those defects sites would have to be disregarded where the H does not stick (41%). This corresponds to a concentration of
2.62 × 1022 /cm3 or
5 × 105 possible locations in the oxide of a
100 nm
100 nm
2 nm device. Note that a defect as shown in Fig. 6.5 would possibly not have the exact same step height in TDDS or RTN measurements when the H atom is at two distinct
sites in the oxide, especially since the impact of the charge is exponentially dependent on its depth. Although, the distance for the relocation is considered to be small and moreover its direction should be statistically distributed, e.g. not necessarily perpendicular to the
interface. However, also a relocation parallel to the interface could potentially influence the peculation path in small devices, altering the step height. Due to thermal broadening and measurement limitations, the step height is naturally slightly distributed in experiments.
Thus a defect as in Fig. 6.5 could well be imagined to be responsible for the seen step heights in measurements, therefore, in the following, it will be investigated further.
Figure 6.8: Example of an alternative four-state model with thermal barriers too low to be detectable in measurements. Barriers lower than 0.22 eV have transition rates in the sub-nanosecond regime too fast to be detected in our measurements. The capital letters each indicate one O atom the H can attach to.
For twenty possible candidates of an alternative four-state model using only the H hopping transitions (see Fig. 6.3), combinations of transitions were explored that would allow for a construction of a stable four-state model (possibly also including volatility). Therefore, for suitable transitions, it was also checked where the H could further hop after the first transition. The method is the same as in the previous section: NEB calculations were carried out to determine the barriers to reach the ten nearest neighbors. The lowest barrier found was always considered to be the most probable transition. If more than one barrier of very similar height is found, of course, both of them have to be taken into consideration.
This leads to a very complex interplay of the involved barriers. Using the calculated barriers it was not possible to construct a simple defect similar to that shown in Fig. 6.7 featuring the barrier heights required by the four-state model. The construction of such a defect mostly fails for two reasons: On the one hand, for many possible combinations in one of the four involved states, a barrier to hop away from the actual four-state cycle is too low. Therefore, this four-state ensemble would not be stable. On the other hand, in stable four-state defects, the transition barriers between the respective states are often much too low, making the transition between these states too fast. According to eq. (5.1), barriers lower than 0.22 eV have transition rates in the sub-nanosecond regime, which is certainly not discernible in our measurements. An example of such a defect is shown in Fig. 6.8. Here the capital letters each indicate one O atom the H can attach to. The barriers between the positively charged states A and B are negligible. In the neutral state, the barriers are in the range as discussed above, where the transitions would occur within nanoseconds. This system could only act as a three-state defect at lower temperatures. If active, at room temperature this defect would act as a two-state defect with two possibilities to reach a volatile state when hopping to the O atoms C or D.
Figure 6.9: Example of a defect that would in our measurements act as a three-state defect at room temperature. The capital letters each indicate one O atom the H can attach to. Again, the barriers between the positively charged states A and B are negligible. In the neutral charge state the H does not favorably undergo the transition between A and B directly but preferably via a third state C. However, this state itself is clearly unstable given the calculated barriers to the states A and B. This defect also features two possible volatility transitions to the states E and F (preferably reached via the unstable state D).
Of all the possible combinations in the presented data set, only one could be constructed that would at least act as a three-state defect at room temperature. This defect is depicted in Fig. 6.9. Again, here barriers between the positively charged states A and B are negligible. For the neutral charge state, we find the interesting case that the H does not favorably undergo the transition between A and B directly. The barriers are considerably lower when the transition happens via a third state C. This state itself is however clearly not stable given the calculated barriers to the states A and B. Therefore, the defect could in principle act as a three-state defect (see Fig. 3.3 (left)) at room temperature. Also, a possible volatility transition starting from the positive state B could be found. Again, the direct transition to the states E and F is higher in energy than hopping via the (unstable) state D. The total barriers for this reaction are in the range where volatility transitions were assumed in the previous chapter. The barrier to return from this volatile states is 0.55 eV though, which according to eq. (5.1) would be a time constant of 0.65 ms and therefore outside of the volatility detection window specified in Section 5.4 and Fig. 5.9.
The findings show that the suggested alternative using H hopping transitions instead of puckering does not seem suitable for constructing the four-state model. Even though twenty possible initial locations were investigated, no fully satisfactory candidate could be
constructed. The limiting factor is that such a candidate would have to have high enough barriers separating the different states and even higher barriers for leaving the four-state cycle. Given the rather low for both charge states determined earlier in the present
chapter, this does not seem very likely, due to the high number of barriers which could play a role. Using the distribution for the minimal barriers calculated in the previous section (see Fig. 6.3) one can
assume the possibilities to encounter suitable four-state defects. Recall that the normal distribution would allow for negative barriers, whereas the Weibull distribution does not. For the following considerations the Weibull distribution fits, as shown in Fig. 6.3, are used. Let us assume the limits for measurable defects between 0.22 and 0.9 eV in the active region (
and
) and barriers larger than 0.9 eV for the transitions when
hopping away from the defect location (in this context the volatility transitions). These barriers correspond to time constants between nanoseconds and several minutes at room temperature and volatility transition time constants of at least several minutes or larger. Leaving
aside the volatility barriers, the above assumption results in
13% of the possible locations having the right barriers for a measurable four-state defect.
However, clearly, the limiting factor is the numerous volatility barriers that are on average too low.
For the sake of argument let us assume that the H atoms do not hop very far during the volatility transitions. When starting from one bridging O in our structures, there are on average eight possible volatility transitions with a hopping distance lower than 4 Å
and mostly more than twenty within a 5 Å range. The possibility of the volatility transition to have a higher barrier than 0.9 eV is just 8% for the positive barriers (though
27% for the neutral barriers). Assuming eight volatile locations the atom could hop to, which
all need to have higher barriers than 0.9 eV, the possibility to encounter a suitable defect drops to
6 × 10−26 (
2 × 10−65 when considering twenty neighbors).2 Since the corresponding defect densities to these probabilities would be many orders of magnitude lower than atoms present in the oxide of a typical MOSFET device, this illustrates that an alternative four-state model
constructed by only assuming H hopping transitions is not a good candidate to overcome the shortcomings of the four-state model (including volatility) as described in the chapters 4 and 5.
6.6 Conclusions
The main implications for the H release model have already been made in Section 6.3, showing that most probably H is not the sole exchange mechanism in the H release model. The considerations above clearly
show that the attempt to construct an alternative four-state model consisting only of H hopping transitions is not very promising. However, the finding in this chapter links the NBTI four-state model (including volatility) to the H release model. We can imagine the NBTI defect as a special case within the H release model. We have seen that the barriers for the volatility transition in Chapter 5 were on
average considerably higher than the H hopping barriers in this chapter (compare Fig. 5.7 to Fig. 6.3). Note that the defects in Chapter 5 were all created using a long bond criterion. We, therefore, can conclude that a strained bond seems to provide larger binding energies for the H atom. Hence, if the additional circumstances for a four-state defect
are met, an H trapped in such a location is able to function as an NBTI-defect characteristic for the recoverable component of NBTI. Strained bonds which are not able to function as an NBTI four-state defect could be imagined to act as the H release or trapping sites within the H release model. Weaker bound H atoms, on the other hand, can constantly hop through the oxide and contribute to the H transfer, thereby providing a possible link between the recoverable and the permanent
component of NBTI.
On the other hand, the findings indicate that H is very mobile in the oxide. It would, therefore, be worth to investigate possible reactions involving two or even more H atoms. A possible mechanism explaining volatility involving multiple H atoms is sketched in Section 6.4. It is, however, impossible to give reasonable assumptions for the possibilities of the involved reactions to occur without additional modeling. It is therefore essential that this alternative model should also be subjected to further investigation.
7 Non-Parabolic Potential Energy Surfaces
The concept of potential energy surfaces (PES, see Section 2.2) has been used throughout the previous chapters. The PES describes the energy of a system of atoms in terms of their position. For a three-dimensional structure
consisting of atoms, the PES, therefore, is a
dimensional object. In the previous chapters we made two assumptions to facilitate the treatment of
transitions involving charge capture and emission:
-
1. A charge capture or emission transition between two states happens along the direct (i.e. the shortest) geometric path interlinking these two states.
-
2. The PES in each charge state can be described as a harmonic oscillator, i.e. the PES along the transition path can be approximated by a parabola.
The first assumption reduces the -dimensional problem to a one-dimensional one since the trajectory of all atoms is well defined by the initial and final configuration. The second assumption makes it possible to approximate a PES by a parabola using just two points, one being the minimum. This
approximation has been widely used throughout the literature [105, 219–225], to list some examples. However, since it is possible to sample the one-dimensional PES interlinking the two states in
greater detail, in this chapter we will have a closer look at the shapes of the PESs. We will refrain from the above assumption number two (the PESs being harmonic oscillators) and investigate the shapes of the PESs in more detail. However, the calculations in this section
were all carried out for the direct path between two states, in other words, assumption one is still presumed valid in the following.
For an approximation, one has to keep in mind that the NMP-theory is a quantum mechanical theory of charge capture and emission events. In principle, a full quantum mechanical treatment would be possible if the analytic solutions (eigenfunctions) to a potential were known. Unfortunately, this is only the case for a very limited number of analytic problems. For a generic shape of the potential, they would have to be calculated numerically for each PES. We will, therefore, use the NMP-theory in its classical limit (see Section 2.2.1) again, as already done in the previous chapters. This neglects a small effective barrier lowering due to tunneling effects [YWJ3]. However, we assume this effect to be of the same order of magnitude for all the PESs and their approximations studied in this chapter. Therefore, when comparing the different approximations or reaction paths to each other, the comparison should not depend strongly on this effect.
PESs were calculated for four different defect types (see Fig. 7.1) in : the oxygen vacancy (OV), the hydrogen bridge (HB),
the hydroxyl-E
center (H-E
center) and a fourth defect related to the H-E
center, but where the
hydrogen (H) atom becomes interstitial when charged neutrally (NIH). The NIH is similar to defects discussed in Chapter 5, 6 and Section 8.2 which feature an interstitial H
in the neutral charge
state. Since we are dealing with amorphous
, the PESs vary from structure to structure. Therefore, for
amorphous structures, the results are always distributed and comparisons have to be carried out at a statistical level. The following study comprises 11 HB defects, 25 H-E
defects, 10 NIH defects and 12 OV defects to provide statistical data.
Figure 7.1: Schematics of the different defects used for the calculations in their neutral charge state. The hydrogen bridge (HB) (a) forms if an oxygen atom is replaced by a hydrogen. In the case of the hydroxyl E center (H-E
), an H atom is bound to the O atom in its positive state, breaking one of the Si-O bonds in its
neutral charge state (b). As shown in the previous chapter, the H atom is always bound to an O atom in the positive charge state. This is often not the case in the neutral charge state. Example (c) shows a defect
where the H becomes interstitial when neutrally charged (NIH). The oxygen vacancy (OV) (d) forms if an oxygen (O) atom is missing.
Figure 7.2: Two charge states of the H-E center calculated using DFT, neutral (left) and positive (right). H atoms are shown as silver,
Si atoms as yellow and O atoms as red. The localized highest occupied orbital is shown as the turquoise bubble for the neutral charge state while it represents the lowest unoccupied orbital for the positive charge state. In the middle, an example PESs of the two
states is shown as a function of the reaction coordinate. In the classical limit of the non-radiative multiphonon transition, charge capture takes place at the intersection of the two PESs. The intersection point determines the barrier
that has to be overcome for this reaction.
The two approximations discussed in this work are each fitted to the two “fitting-points” shown in this graph, calculated using the two minimum configurations. Interaction with an electric field shifts the PES of the charged state by
, changing the intersection point and therefore the barrier
heights.
For those defects, we will discuss the PESs and their approximations in their neutral (), positive (
) and negative (
) charge states, as well as the transitions between
and
. Finally, we also investigate transition
barriers when all three charge states are considered simultaneously for the aforementioned defect types. Here the possibility of direct transitions
(double capture/emission) is of special
interest, since double capture and emission is an effect that has been reported in measurements [68] (see Fig. 1.6).
7.1 Simulation Framework
Figure 7.4: Depending on the applied bias conditions, the PESs move up or down, thereby changing the energy barrier that has to be overcome for charge capture or emission. The above plots show the reaction time constants for hole
capture and emission ( and
) at
=100 °C for the corresponding PESs in Fig. 7.3.
It can be seen that due to their exponential dependence they are very sensitive to a change of the barrier height. To quantify the improvement, an L
norm for
(similar for
) is shown as score function. Since the depicted graphs
are only one example for each defect type, a comparison has to be done on a statistical level, as it is done in Fig. 7.5.
The normalized reaction coordinate (NRC) is defined as the normalized -dimensional atomic displacement vector between the minima of the respective charge states
(see Fig. 7.2). For constructing the PES this displacement vector was used to interpolate configurations between the two states (range 0.0 to 1.0), or extrapolate configurations in the range -1.0 to 0.0 (or 1.0 to 2.0
respectively). The PES was then calculated by computing the energies for 30 configurations along the NRC (single-point DFT calculations, see Section 4.3.1) in the range -1.0 to 2.0, and spline interpolation
in between (see Fig. 7.3). These DFT-PES (
) were taken as references to evaluate the quality of the
different approximations relative to
.
The s and their approximations are then used for calculating the transition barriers between the different states (and consecutively
and
). For this purpose, we no longer assume a pure a-
structure as for the DFT calculations, but rather a
Si/
model as would be the case for silicon (Si) based
electronics. In this model, described in more detail in Appendix A.4, the Si/
band offset is set to 4.5 eV and the defects sit
in
but capture and emit their charges from/to the Si
conduction or valence band respectively. For all these calculations we use a semiclassical approach based on [105] and [103]. When an electric field is applied, as would be the case under operating conditions in electronic devices, the PESs shift relative to each other along
the y axis, changing the reaction barrier (see Section 2.2.2 and Appendix A.4) and therefore
and
. An example of
and
calculated using the PESs of Fig. 7.3 is depicted in Fig. 7.4. Note that the values of
and
change by multiple orders of magnitude in these plots
because of their exponential dependence on the reaction barrier. All
and
calculations have been carried out at four different
temperatures (
= 50 °C, 100 °C, 150 °C and 200 °C) to also
capture the temperature dependence of this effect.
7.2 Parabolic and Morse-Approximation
In order to obtain , 30 points were calculated along the normalized reaction
coordinate for each PES. However, this is computationally demanding, which is why a good approximation derived from few fitting-points would be desired instead. For the calculations in this
work, the analytic functions of the parabolic approximation (
) are calculated by fitting the parameter
in
using two points for each parabola (the respective equilibrium configurations of the two charge states) [3, 101] (see Fig. 7.2). The coordinate in eq. (7.1) thereby always refers to the minimum of the PES of respective charge state. As demonstrated in Fig. 7.3,
tends to underestimate the crossing point if compared to
. This observation holds true for all defect types
investigated in this chapter. Note that this observation also would hold true if the second fitting point (see Fig. 7.2) would be chosen closer to the respective minimum, for example at a normalized reaction coordinate of
0.5, i.e. in between the minima [YWC6]. Our calculations show that the curvature of the
around the minima is more than quadratic, as can be
seen in Fig. 7.3 (and also later in Fig. 7.8 for the transition involving the negative charge state). A parabola will consequently always lie lower than the
curve.
Figure 7.5: Double logarithmic correlation plots for the values of for hole capture at
=100 °C for all the defect types discussed in this chapter. Correlation of
calculated using
and
calculated using
(top, grey) or
(bottom, turquoise) are shown. When the result for
calculated
using the
, and the result
using the approximation are equal, the respective point would lie along the diagonal, therefore the off-diagonality can be used as a criterion determining the quality of the fit. It is clearly visible
that
tends to be underestimated in the parabolic approxima-
tion. To quantify the improvement an L
norm for the distance to the diagonal which is shown as a score function. Whereas there is
nearly no difference for the OV, there is a considerable improvement in the other cases.
Figure 7.6: Correlation plots for the slope of at different temperatures. The re-
sults using
are compared to the ones obtained with
(top, grey) or
(bottom, turquoise). It is clearly visible that
is overestimated in the parabolic approxima-
tion. Whereas results change for the worse for the OV (here the parabolic approximation already gives satisfactory results), there is again considerable improvement for the H-related defects when using the Morse-approximation. To quantify the improvement,
again an L
norm for the distance to the diagonal is shown as a score function.
A different approach to approximate the PESs is to use a Morse-potential, which is not symmetric around its minimum. This should capture better the shapes of which are also anharmonic (see Fig. 7.3 and Fig. 7.8).
Here the parameter is the value the potential converges to for
. In the case of the Morse-potential
describing a chemical bond,
is often referred to as dissociation energy. For the Morse-approximation the potential
was used to fit the data,
being the new minimum configuration of the new charge
state. In other words, for a transition at
(at the “new” optimum configuration), the “old” potential
has reached 50% of the dissociation energy. This assumption has led to satisfactory results for the Morse-approximation. It fixes the parameter
to
, making
the determining factor for the Morse-approximation. We then use the same fitting-points again as for
the parabolic approximation (see Fig. 7.2).
The Morse-potential would also allow for a simple quantum mechanical treatment of the transitions since this potential has an analytic quantum mechanical solution. Quantum mechanical transition rates, for example, were calculated in [226]. Here, however, we focus on the classical limit of NMP-theory. The main impact on barrier heights when using quantum mechanical transition rates would be a small decrease of the effective barrier height due to tunneling.
As can be seen in Fig. 7.3, for the H-related defects, the intersection is better approximated by the Morse-approximation than by the parabolic approximation. However, this does not seem to apply for the OV.
Furthermore, one can see that the Morse-approximation does not properly capture the neutral PES in the range . Note that the slope around the minimum of each PES is
more than quadratic in all shown examples. Thus, a parabolic approximation is not able to capture this behavior, regardless of the parameter
in eq. (7.1). The crossing point is hence
always underestimated when using
. Although the differences in the respective barriers are
only in the range of 0.1 eV, this leads to large differences in capture and emission times, because of their exponential dependence
on those barriers. This will be discussed in the following.
7.3 Capture and Emission Times
We will now discuss and the two approximations discussed above for
calculating
and
for several defects and temperatures. It should be noted
that due to the interaction with a whole band of states (see Section 2.2.1) the dependence on the barrier height to overcome is not as simple as for the purely thermal barriers in the chapters 5 and 6. It is therefore not possible to give a simple formula similar to eq. (5.1) for converting
the NMP barrier heights into time constants or vice versa.
An additional aspect considerably affecting and
is strong and weak electron-phonon coupling (see
Section 2.2.3). This effect is responsible for many transitions being barrier-free at several bias-conditions. Interestingly, whether a defect is in the weak or strong electron-phonon coupling regime is nearly independent of the chosen approximation for the PES, and also explains the results seen for the OV.
However, whether a defect is in the strong or weak electron-phonon coupling regime is only partly an inherent property of the
defect. It is strongly dependent on the energy difference between the two minimum configurations, as can be seen in Fig. 2.5. This, again, depends on the band-gap or band-offset in the case of material interfaces (see
Appendix A.4), which is different for each material combination. Furthermore, when an electric field large enough is applied (evoking a shift,
), the PESs can always be shifted relative to each other so
that the other coupling-regime is reached. However, note that Fig. 7.3 and Fig. 7.8 are plotted for a
where both minima lie at the same energy. This shift is by
far the highest for the OV which, without an applied
, would usually lie in or very near to the weak coupling
regime.
7.3.1 Transition 
Figure 7.7: Arrhenius plots for the four investigated defect types showing the temperature dependence of at a shift
= 0.3 eV. In such plots, the slope of a fitted straight-
line determines the activation energy
. The lines are a least squares fit to the data points, also providing the slope to calculate an average
. To quantify the quality of the approximations, an L
norm for the differences to the results using
(black) is depicted as score function. As already seen in
the previous figures, the results for the OV do not depend much on the approximation used. For the other defect types the Morse-approximation gives again much better results than the parabolic
approximation.
The parabolic approximation tends to underestimate the crossing point of the two PESs (see Fig. 7.3). On the other hand, the Morse-approximation does not seem to satisfactorily capture the neutral PES in the range
. Nevertheless, we will see in the following that this does
not have a significant influence on
and
. The PESs from Fig. 7.3 lead to
and
plots as depicted in Fig. 7.4. As can be seen, the underestimation of the crossing point by the parabolic approximation causes an underestimation of
and
of several orders of magnitude. Although the parabolic
approximation gives good results for the OV, it fails by several orders of magnitude for all the H-related defects. One can see a considerable improvement when the Morse-approximation (7.2) is used, in agreement
with what has been reported in [227]. The good results for the parabolic approximation for the OV are, however, mostly due to the OV being preferably in weak electron-phonon coupling (see Section 2.2.3).
An overview of all defects of one type is given in correlation plots in Fig. 7.5. Due to the amorphous nature of the simulation cells, the results are spread out over a wide range. The off-diagonality can be used as a
quality criterion for an approximation since a perfect agreement between the compared values would lie exactly on the diagonal. For the parabolic approximation, a clear off-diagonality can be observed. The quality increases when using the Morse-approximation, but the overall agreement is weakest for the NIH defects. For this defect, the displacement of the involved atoms (the absolute reaction coordinate) is the highest of the four studied defect types. Therefore,
the adiabatic approximation might already be problematic [183]. Furthermore, also the errors when linearly interpolating the PESs in our method (see Section 7.1) are presumably highest for this defect, which also might show the limitations of our approach. Fig. 7.5 only shows the results for
=100 °C. Calculations show that the results are similar for the other three temperatures
(50 °C, 150 °C and 200 °C). Moreover, this figure shows the different
of the hole capture transition
. Results are similar for the reverse transition
and
.
In Fig. 7.7 the temperature dependence of is analyzed using Arrhenius plots for a value of
0.3 eV. In this kind of plots
is plotted against the inverse temperature
[116, 219]. For a single rate-limited thermally activated process, an Arrhenius plot gives a
straight line, from which the activation energy
can be deduced by its slope. A least squares linear fit for
is provided for the
calculated using
, the parabolic approximation, and the
Morse-approximation. Again we see that the Morse-approximation is in better agreement with the results calculated from
. This result also holds true for other values of
and moreover for the reverse transition
.
Finally, a good approximation should also be able to reproduce the dependence of the barrier heights of the electric field. This dependence essentially determines the slope of curves [3], i.e. the slope in Fig. 7.4. For each
curve we determined the
by fitting a straight line with a least
squares fit to the range
= 0.3 to 1.0 eV, in other words the right
branch in Fig. 7.4. The slope for the defect types and for different approximations is again plotted in correlation plots (Fig. 7.6). Like in Fig. 7.5,
gives a poor match to the behavior calculated using
. For the H-related defects, the agreement again is better
for the Morse-potential. For the OV, however, this does not hold true. Here the result only depends weakly on the chosen approximation due to the OV being mainly in weak electron-phonon coupling
in our model. Fig. 7.6 again shown an example and results are similar for other temperatures and for a fit to the range
−0.3 to −1.0 eV, i.e. the left branch in
Fig. 7.4. Moreover, Fig. 7.6 shows the hole capture transition
. It should be pointed out that the results also
agree for the reverse transition
and
.
Figure 7.8: The corresponding PESs for the transition of Fig. 7.3
and their approximations, depicted for a shift where both minima lie at the same energy. As in Fig. 7.3 each graph is an example of one of the investigated
defect types. PESs for the transition
tend to be slightly more complicated than
for the transition
. PESs tend to show saddlepoints or even
local minima, as visible here for the H-E
and OV. This makes a good approximation even more challenging. However, here the Morse-
approximation also seems to give better results.
Figure 7.9: Same as Fig. 7.5 but for the transition . Due to the more complicated shape of the PESs
for this transition the quality of the two approximations decreases. Nevertheless, the Morse-approximation still gives better results than the parabolic approximation for all investigated defect types. To quantify the improvement, an L
norm for
(similar for
) is shown as score function.
7.3.2 Transition 
The situation for the transition is a bit more complicated, since
the involved PESs tend to have more complicated shapes (see Fig. 7.8). PESs showing additional local minima are not rare in the negative charge
state. However, one has to keep in mind that this could also partly be an artefact of the assumption of the configuration coordinates when using linear interpolation (see Section 7.1 and Chapter 8.2).
Results for the different approximations are very similar to the transition. The
are steeper than the parabolic approximation would
predict, leading to an underestimation of the capture and emission times by the parabolic approximation. As already seen for the transitions
, correlation plots for
(Fig. 7.9) show, that the Morse-approximations yield better results also for this transitions. However, as the score function indicates, due to the more complex nature of the PESs, the approximations for the transition
are in general of poorer quality than for their
counterpart (see Fig. 7.5). Fig. 7.9 shows the results for
=100 °C. Results are similar to the other three temperatures (50 °C,
150 °C and 200 °C), for which results were calculated. Fig. 7.9 shows the different
of the electron capture transition
. Note that the results are similar to the reverse
transition
and
.
As in the previous section findings for the activation energies (Arrhenius plots) and the electric field dependence also show that the Morse-approximation yields better results than the parabolic approximation. Therefore, it is not necessary to show the redundant
corresponding plots to Fig. 7.7 and Fig. 7.6. However, it should be noted that in the case of the transitions the approximations are in general slightly
poorer than for the
transitions. As in the previous section, the
results are similar for the other investigated temperatures and for different shifts
, as well as for the reverse transition
.
7.4 Double Capture and Emission
When two charge states are considered, as we have done up to now, in our approximation of the transitions there is only one
reaction path in and out of one state and so reaction dynamics stay simple. Considering three charge states, dynamics become more complicated since there are always two paths entering and leaving
one state and, moreover, also two competing pathways for reaching another state (see Fig. 7.10). Consider, for example, a positively charged defect becoming negatively charged. The first possibility is for the
defect to go via the neutral state by capturing an electron and consecutively capturing a second electron to reach the negative charge state (). However, one could also
imagine a pathway where there are two electrons captured simultaneously for a direct transition
.
To our knowledge, there are very few works dealing with this simultaneous double-capture or emission in NMP-theory [228]. For an estimation of whether simultaneous double capture/emission events could be found in the discussed defects, we now leave aside the
capture cross-section and attempt frequency, which would differ between a single-particle transition and simultaneous double capture or emission event involving two charged particles. This is justified since and
only depend linearly on capture cross-section and
attempt frequency, but exponentially on the barriers. Consequently, the following considerations on reaction times for double capture and emission can always be seen as an infimum when compared to the single-particle processes. In the following, we will use the PESs
calculated by DFT to estimate whether a double capture or emission is likely to occur in the different defect types by comparing the barrier heights that have to be overcome for the different reaction paths.
Figure 7.10: Top: The six possible transition paths when all three charge states are considered. Depending on the actual barrier heights, only a few of these pathways are favorable. Considering all three charge
states there are always two different pathways connecting two states. For example, the transition can either procede
directly or via an intermediate step along the path
.
Bottom:
for the transitions
(left),
(middle) and
(right) of one selected example H-E
center. Note that the PESs
are different for all three transitions because the reaction coordinate is always assumed to be a direct path between the two states.
Figure 7.11: Barrier plots showing all six barriers for different . Blue transitions (full symbols) make the defect more neg-
atively charged, red (empty symbols) more positively. The colors and symbols were chosen according to Fig. 7.10, which therefore can be used as a legend for these plots. On the right-hand side, the
corresponding capture and emission time plots are presented. The possible observation window is indicated by the colored area.
Top: Plots deduced from the PESs in Fig. 7.10.
Bottom: Example barriers for one OV defect.
When an electric field is applied, the PESs in Fig. 7.10 shift relative to each other along the y-axis (), thereby changing all six transition barriers. Depending on
the charge state and reaction path can change completely.
We consider a state stable if:
-
• Both time constants for leaving the state are higher than the time constants to get there.
-
• The time constants to leave the state exceed the measurement times. In the following a maximum time of 106s is used. This is approximately 11.5 days.
This definition deliberately does not include the minimum energies of each involved PES, as it is common in formation energy plots based on eq. (A.1). These plots are very frequently used to determine the relative stability of defect charge state calculated by DFT. However, they only consider the minimum energies of each PES, not taking into account the transition barriers between them. A well-known example is the so-called negative-U center [184, 185], which is defined by formation energy plots not showing a stable neutral state. As already discussed in the chapters 5 and 6, this does not include any information about possible metastable neutral states. Therefore, note that the sole negative-U property of a defect is no sufficient explanation of double capture or emission. Chosen pragmatically, the above definition also takes into account the transition barriers.
Let us consider again the PESs from Fig. 7.10 (bottom) as an example, where a particular defect is shown for 0 eV. The energetically lowest configuration for
this particular defect, at the chosen
, is the negatively charged state. In Fig. 7.11 (top) we see all six barriers calculated using the PESs from Fig. 7.10 for different
. Therefore, Fig. 7.10 (bottom) corresponds to Fig. 7.11 (top) at
= 0. One can see that the negative charge state is the lowest,
however, barriers in and out of this defect are very high and therefore it is very unlikely that the defect would become negatively charged in the first place. However, the defect can switch between
and
depending on
. We see that the curves for the barrier heights for the
competing transitions
and
intersect at
0 eV. For negative values of
the dominant transition is
, making the defect preferably positive. For
positive values of
, we find the exact opposite, making the defect preferably
neutral. It can be clearly seen that the barriers for a direct transition
are by far too high and always higher than the
corresponding barriers for a two-step process via the neutral state
. This observation will also hold true for all H-related defects in the following.
For the OV defect presented in Fig. 7.11 (bottom) it seems as if a double capture/emission is favorable. However, note that both transitions into the neutral state are practically barrier-free. This defect,
therefore, would always tend to stay neutral. If a transition of any kind occurred, it would immediately go back to the neutral state without a significant barrier. This behavior is due to the OV being in the weak electron-phonon coupling regime (see Section 2.2.3) for those transitions.
Rapid changes of , as they happen in oxides of electronic devices under
operating conditions, can force the defect to change its preferred charge state constantly and quickly. A defect can thereby sweep through the entire range of the plots in Fig. 7.11 or Fig. 7.12. This could well cause a defect to go from preferably positively charged for one value of
to preferably negatively charged for another value of
or vice versa. To reach the respective other state, the defect
then has to capture or emit two charge carriers. As discussed above, this could either happen consecutively (via the third state) or simultaneously. It is of special interest if we could find configurations in which the simultaneous double electron capture or emission would
be the dominating path. This implies that the barrier for this transition is lower than the determining barrier (i.e. the higher one) of the alternate two-step reaction.
Figure 7.12: Two defects capable of cycling between all three investigated charge states when swept through different shifts , an example H-E
defect (top) and one example HB defect (bottom).
Top: The H-E
defect can theoretically cycle between all three charge states in measurements since all curves
lie partly within the observation window. This is necessary to be able to explain TDDS data as in Fig. 1.6.
Bottom: The HB defect, which would preferably be positively charged for
0.1 eV and preferably neutral for higher val-
ues of
. However, in this defect, the barrier heights in and out of
the negative state are not so much higher and therefore reachable. For large negative shifts, this defect potentially allows for “pseudo-simultaneous double hole capture”.
In all the H-related defects studied in this chapter we could not find one that fulfills this criterion, thus simultaneous double capture or emission should be unfavorable in these defects. On the other hand, for all the OV defects simulated (see Fig. 7.11(right)) this criterion is actually fulfilled; however, even these defects would not undergo double capture or emission. Note that in this figure (which is characteristic for the OV defects) both transitions to the
neutral state are barrier-free (because of being in the weak electron-phonon coupling regime). Therefore, the defect will never be charged under these conditions and even if a charge capture or emission
event of any kind (single or double) would occur, the defect would immediately go to the neutral state again. This is similar for all the OV defects studied. Therefore, in all studied defects in this
chapter, we could not find one that would allow for any direct transition. Thus, we can conclude that single charge capture or emission transitions dominate and that transitions between the states
and
always happen as a two-state process via the neutral charge
state. This allows us to discard the direct transitions of which the prefactors are uncertain and only use
and
for the single capture or emission as already investigated
in sections 7.3.1 and 7.3.2. In Fig. 7.11 and Fig. 7.12 the
and
are calculated in an example device using the NMP-rates
as described in Section 2.2.1. It can be clearly seen that for these transitions the conversion between barrier heights and time constants
is not as simple as for the purely thermally activated transitions. Also in these plots, it is
possible to define the limits of the observation window. In the following they are assumed as 106s (approximately 11.5 days) as upper limit and 10−4s as lower limit. The lower limit results from typical measurement resolutions in RTN
measurements, the measurement delay in TDDS when switching from the stress to the recovery (measurement) phase is typically a bit lower (10−6s). All presented barrier and
/
plots in this chapter were calculated for a temperature of
100 °C.
Let us now take a closer look at Fig. 7.12, in which one example H-E and one example HB defect are shown. These two examples exhibit a more complicated
behavior than the ones discussed above. For the shown H-E
the preferred charge state is negative for
0.6 eV and
for lower values. Barriers to reach
are, however, also within the measurement window and state
is possibly accessible for larger negative values of
. For the example HB defect in Fig. 7.12 (bottom) the preferred states are
for
0.25 eV and
for higher values of
, the barriers in and out of the negative state are also low
enough that it could be potentially reached. Therefore, both defects could switch between all three charge states when sweeping often between different
. An interesting feature should be noted for Fig. 7.12 (bottom): Given that the defect reaches the negative state and then sweeps to the very left of the plot (
−0.5 eV) both barriers for hole capture
are very low. Therefore, these reactions could happen nearly consecutively after each other which might well be faster than typical measurement resolutions [7, YWJ1]. The same holds true for the very right of the plot (
0.75 eV). In these regions, the time
constants for the transitions are lower than the typical observation window in our measurements. In a measurement, it could, therefore, seem as if the defect goes instantly from
to
even though it actually was a two-state process. Note that in TDDS analysis this behavior would result in a step with double step height, and would, therefore, most likely be mistaken for a single transition. In the following we will refer to this process as
pseudo-simultaneous double-emission or capture. This defect would, however, not double capture or emit during RTN analysis since there are no sweeps of
during such a measurement. Nevertheless, it is an example
of a defect which is able to cycle between all three charge states within the given range of
. This is a requirement if a defect was to explain the TDDS
double-emission seen in Fig. 1.6.
Figure 7.13: One example H-E defect and one example HB defect capable of cycling
between all three investigated charge states, which would, however, preferably cycle between the states
and
. This is due to the time constants for the transition
being much higher than
.
A very interesting feature should be noted in the right panel. In this HB defect, both crossings define where the transitions are in thermal equilibrium (the crossing of both lines with diamond markers or quadratic markers respectively) are in close proximity to each other. Therefore, at a shift
of
0.05 eV this defect could potentially
also switch between all three charge states in RTN measurements. However, due to the involved barriers, this is unlikely, as discussed in the text.
|
Type |
defects |
3 states |
2 states |
1 state |
|
HB |
11 |
11 |
0 (0/+) |
00 (0/+) |
|
H-E |
24 |
16 |
7 (0/+) |
01 (+)0/ |
|
NIH |
10 |
00 |
5 (0/ |
05 (0, |
|
OV |
12 |
00 |
0 (0/+) |
12 (0)0/ |
Table 7.1: Statistics for all the studied defects indicating whether the defects are capable of cycling between all three charge states, assuming 106s as upper limit and 10−4s as lower limit for the time
constants. We see that all HB defects and also two thirds of the H-E should theoretically be able to reach all three charge states when sweeping through the entire
range of
. This behavior is required to explain TDDS data as in Fig. 1.6. Interestingly, there is a clear preference of the two-state defects: the H-E
are switching between
, whereas the NIH tend to switch between
. The preferred charge states are indicated
next to the numbers.
Assuming the measurement window defined above we can now have a look at how many defects would be able to cycle within all three charge states. These statistics are summarized in Tab. 7.1. We see that the number of defects that are able to cycle between all three charge states (example barriers shown in Fig. 7.11 (left)) under the previously defined conditions is very different for the several defect types. All of the investigated OV tend to stay neutral (example barriers in Fig. 7.12 (left)). In order to explain TDDS data as seen in Fig. 1.6 defects which can cycle through all charge states when sweeping through the entire range of are sought. As already mentioned, this is found neither for
the OV nor for the NIH defects. On the contrary, the investigated HB defects are all capable of reaching all three charge states. For the H-E
all possible combinations occur, however, also for this defect two thirds are capable of cycling. Interestingly, there is a clear preference for the two-state defects: The H-E
are switching between
, whereas the NIH tend to switch between
. It should be mentioned that the label
“three-state defect” in the above sense means that the defect is potentially able to reach all the charge states. It does not provide any information on the defects preferred behavior. For the
majority of the three-state defects it was found that even though they can potentially reach the negative charge state, they preferably would just cycle between the state
and
. This is a very important finding supporting the NBTI model described in Section 3.1. This can be seen for two example defects in Fig. 7.13 in which the negative state
is theoretically accessible, but not favorable.
A very interesting feature can be seen in Fig. 7.13 (right). Note first, that the crossing of the related capture and emission curves define the thermal equilibrium of the respective transition. In this example
HB defect both these crossings lie in close proximity to each other. Therefore, at a shift of
0.05 eV this defect could potentially switch between all three charge states in RTN measurements. The proximity is required since the RTN measurement window is limited to an area adjacent to these equilibrium crossings (see Section 1.2). Note, however, that the time constants of the two intersections are separated by many orders of magnitude. The crossing for the transitions
lies at very high time constants. Thus,
this transition would just occur a few times in very long measurements. Therefore, if double capture/emission happened in such an RTN measurement it would quite likely be missed due to the low number of occurrences.
This illustrates that the possibility of a defect to cycle within all three states in RTN analysis is very low. To frequently appear in one RTN measurement trace, all four involved barriers would need to have very similar capture and emission time constants at the selected measurement voltage. This is a very limiting criterion and a possible explanation why, to our knowledge, such measurement traces have not been reported in the literature up to now.
In Tab. 7.1 an overview of the investigated defect sample is given. The finding that a considerable number of defects is possibly able to
cycle within all three investigated charge states is a possible explanation for the defect behavior seen in [68] (see also Fig. 1.6). The effect of
“pseudo-simultaneous” double capture or emission is considered possible, if the second barrier that has to be overcome is lower than 0.5 eV (example barriers in Fig. 7.12 (right)). This is especially interesting since such two-step processes could be mistaken for single charge capture or emission with double step height in TDDS measurements. We see considerable differences in the various defect types. For the OV, since it is always neutral, the situation is clear. For the other defect types,
just a couple of defects could be capable of “pseudo-simultaneous” double capture or emission. Of the defects in this work this is true only for four HB and two H-E defects but not for the NIH. This, however, might be due to the small sample of NIH
defects.
7.4.1 Do Double Positive and Double Negative Charge States Exist?
In this chapter, it was attempted to explain double capture or emission processes by also considering negatively charged defects. Such processes would also be possible, for instance, between a double positive charge state and a neutral charge state or between the
neutral and a double negative charge state. Therefore, it was also investigated whether double charged defects could exist. Certainly, it is possible to create doubly charged structures in DFT and calculate the respective total energies. For the calculation the charge is imposed on the structure as a boundary condition, therefore, the whole structure necessarily holds the double charge. This, however, does
not mean that the double charge is really located at the defect site. It can also be located on a different site or partly delocalized over the whole structure. These calculations were carried out on three
a- structures created as described in Chapter 4, each containing 216 atoms. In these structures an H was placed next to each of the 144 O atoms at a distance of 0.7 Å following geometry optimization in their positive charge state. With just very few
exceptions where the H atom moved to a neighboring O atom, the H stayed at the O atom where it was placed next to. The resulting structures then underwent further geometry optimization when double positively or negatively charged. The resulting structures were then
analyzed on where the wave function of the two electrons or two holes (the two highest occupied or unoccupied states) were localized. In these investigations, no defect could be found on which two holes or electrons were located.
Figure 7.14: Double negatively charged structures containing a defect, an H-E (left) and an H atom sticking to a Si atom (right). The possible negatively charged defects are
discussed in the following chapter and Fig. 8.1.
The second highest occupied state is indicated by the green bubbles, the highest one by the turquoise bubbles. It is clearly visible that the second electron (turquoise) does not localize at the defect site.
Since the structure is forced to a double negative charge by the boundary conditions, the second electron locates on the energetically most favorable position. The two examples above were created from the same structure, but the defect sits at different Si atoms. The Si
atom where the second electron localized was the same in both cases.
When carefully investigating the wave functions obtained by the DFT calculations, one can see that the second charge is either smeared out over the structure or captured at another atom (see Fig. 7.14). It seems logical that a double positive charged defect does not exist since the positive charge arises from the H losing its only electron and it is unclear where the second electron should be taken from. For the negative charge state it seems that, if such a defect exists, the first additional electron tends to occupy the same orbital as the already present electron at the H atom but, of course, with the opposite spin. Therefore, in this case, there is no energy level or orbital left to occupy at the H atom and the second additional electron preferably finds a different location. This could be, for example, a Si with wide O–Si–O bond angle [157]. We can, therefore, conclude from these investigations that if double charged defects exist, their occurrence is at least very unlikely.
7.5 Conclusions
When the PESs are directly interpolated between the minima found for the respective charge states it turns out that the parabolic approximation underestimates the crossing point of the PESs compared to PESs calculated from more DFT points along the direct reaction coordinate. This can lead to underestimation of the capture and emission time constants by the widely used parabolic approximation of several orders of magnitude. A different approximation using a Morse-potential (with also only a single fit parameter) seems to better capture the general shape of the PESs and might, therefore, be a better choice to estimate the PESs. In general, the quality of the approximations is better for the transition between the positive and neutral charge state compared to the transition between neutral and negative. Here one often finds saddle-point-like behavior or even local minima at certain PESs which cannot be fitted using the suggested approximations. This could well be evidence that the chosen direct interpolation for the reaction coordinate might not be an ideal choice.
Furthermore, the charge capture and emission dynamics considering three charge states were also studied. It is of particular interest, if defects are capable of cycling within all three charge
states under typical operating conditions in a MOSFET since this could explain observed double capture or emission in TDDS measurements. It could be demonstrated that this behavior is possible for
HB and H-E center defects. It should be noted that although they can potentially reach the negative charge
state, they preferably would just cycle between the state
and
. This is a very important finding supporting the NBTI model discussed throughout this thesis. Once
more in this chapter, it can be seen that the HB and the H-E
center defects are capable of explaining the observed measurement behavior, whereas the OV
is not. The behavior of the NIH defect seems a bit dubious, this is, however, due to much more complicated defect dynamics as shown in Section 8.2.
8 Conclusions and Outlook
8.1 Conclusions
In silicon-based MOSFET technology, silicon dioxide () still plays an important role in the gate oxide of transistors. Even though nowadays the oxides typically consist of oxynitride and high-k materials, a thin
interfacial layer is usually present.
Unfortunately, the
is typically not defect-free. Defects which are capable of
capturing and emitting charge carriers can interfere with the device electrostatics and cause device failure. This work has mainly focused on the negative bias temperature instability (NBTI), usually
encountered in pMOS devices when a large voltage is supplied to the gate contact while all other terminals stay grounded. An additional problem is that the
in these applications is not in a crystalline form, but
rather is amorphous (a-
). Therefore, defect charge capture and emission times
and all the related defect parameters strongly vary depending on the position of the defect in the host material. This is seen in measurements where capture and emission times are spread over several orders of magnitude.
Furthermore, it was shown in previous works that, in order to explain the observed NBTI behavior, a four-state model as described in Section 3.1 has to be assumed. This model has a set of 13 parameters,
which can be deduced by fitting measurement data. All but two of the parameters can, however, also be determined by density functional theory (DFT) calculations. Thus, with the help of DFT calculations, a comparison of the experimentally and theoretically obtained
parameters can be used to judge whether a proposed defect candidate can explain the experimental results. Though, due to the amorphous nature of the host material, this comparison can only be performed at a statistical level, resulting in a large distribution of the
mentioned parameters. The results obtained in this thesis suggest that hydrogen (H) plays a key role in NBTI. In Chapter 4 it is shown that the oxygen vacancy (OV) defect is not a suitable candidate to
explain the observed measurement behavior, whereas the H containing defects, the hydrogen bridge (HB) and the hydroxyl-E center (H-E
center), are both suitable to do so.
In Chapter 5 an effect not covered by the NBTI four-state model is addressed: Defects repeatedly tend to dis- and reappear from the measurement window, which is referred to as volatility. An
extension to the four-state model is proposed, assuming that the H moves away from the defect site to a neighboring bridging oxygen (O) atom to form a volatile state. Assuming this mechanism, the HB is not suitable to explain this effect, whereas results seem plausible
for the H-E center. Barriers for the proposed transitions are within the expected range for both the
positive and neutral charge state. Though the reverse barriers do suggest that more stable volatility transitions should be able to occur in the positive charge state. Thus, the H-E
center is the only remaining defect candidate which is able to cover all the desired features
and the most promising defect candidate for explaining the measured recoverable NBTI behavior in MOSFETs.
For the permanent component of NBTI an H release model as described in Section 3.2 was used as a starting point for the investigations. However, it could be shown in Chapter 6 that, at approximately every third O atom, there are very low barriers for the interstitial neutral H (H) to bind. Hence, H
would not be able to diffuse very efficiently, contrary to the assumptions when the model was
first formulated. H
transport in a-
would be more a hydrogen hopping from
bridging O atom to bridging O atom as it is already well-known for positively charged H (H
). Whereas for H
nearly all bridging O atoms can take part in this process, for H
it would be only the
59% of bridging O it can stick to. Since the barriers for these transitions are at
comparable heights for both charge states, it is not clear if one of the charge states would dominate the H transport. This component of the H release model presented in Section 3.2 should,
however, be reconsidered given these findings.
The only difference between the H hopping transitions and the volatility transitions for an H-E center is the initial state. Whereas a hopping transition can start from any O in the structure,
the starting point for a volatility transition is an H-E
center having a strained bond. Comparing the H hopping barriers in Chapter 6 with the volatility barriers obtained from the H-E
center in Chapter 5, one can see
that the H hopping barriers are considerably lower. Note, however, that the defects calculated in the respective chapter were all selected using a strained bond criterion. This indicates that the H is exceptionally strongly bound to the bridging O atom at such strained
bridging O atoms. Therefore, if the additional circumstances for a four-state defect are met, an H trapped in such a location is able to function as an NBTI-defect, characteristic for the recoverable component of NBTI. Strained bonds which are not able to function as an NBTI four-state defect could be imagined to act
as the H release or trapping sites within the H release model. Weaker bound H atoms, on the other hand, can constantly hop through the oxide and contribute to the H transfer. In a-
where H is always present, the H atoms would move
through the oxide of a MOSFET transistor by hopping transitions, showing temperature and, for H
, bias dependence. These findings also indicate the following important conclusion: If in an
a-
structure a precursor with the basic features needed for
an NBTI four-state H-E
center defect is present
(an elongated bond and the possibility to pucker as described in Section 4.2.3) and H is present to a certain amount, the H eventually reaches the defect site by hopping transitions, forming such a defect. Thus, one could
imagine the NBTI four-state defect as a special case within the H release model. This interlinks the H release model with the four-state NMP model for NBTI (extended by volatility).
The possibility of H hopping through the oxide means that it could also be imagined that several H reach the defect site. As shown in
Chapter 6.4 a defect receiving a second H would be passivated. When interacting with a third H it could be activated again over a small barrier where two H form an H molecule and diffuse away. This provides an alternative
mechanism for volatility which was not addressed in this thesis. It is however highly recommended to investigate this mechanism further in subsequent research.
In Chapter 7 the assumption of parabolic potential energy surfaces (PES) is questioned. This assumption is widely used throughout the literature and seems natural since a parabolic PES describes a harmonic oscillator. However, when calculating the energies along the direct path interlinking the atomic configurations of the different charge states of the defects it can be seen that the obtained shape seems to be considerably steeper. It could be shown that when assuming a Morse-potential instead of the parabolic shape, the fit with the calculated DFT reference could be improved. In this section, the negative charge state of different defects was also considered. Unfortunately, fits for the negative charge state are in general of worse quality, since their PESs tend to have a more complex shape. However, the finding that a Morse potential yields better results than a parabolic approximation with respect to the DFT reference also holds true for the negative charge states.
The inclusion of the negative charge states makes it possible to investigate the more complex interplay of barriers interlinking three charge states (,
and
). It was shown that such an interplay could provide a possible
explanation for the experimentally observed double capture or emission events. It could be demonstrated that this behavior is possible for HB and H-E
center defects. It is nevertheless important that, although they theoretically can reach all three
charge states within our measurement window, their preferred behavior would be to just cycle between the state
and
. This is a very important finding further supporting the above mentioned NBTI model. The findings
in Chapter 7 are based on the assumption of the direct interpolation between the different energetically relaxed defect charge states. However, this assumption is already questioned by the follow-up work described in the
following outlook.
8.2 Outlook - A Zoo of Different Configurations
The positive and neutral charge states of the H-E center have been discussed in
depth in Chapters 4 and 5, since these are the important charge
states for NBTI. In Chapter 7 the negative charge state was also included in the calculations. Recently it was discovered that more configurations related to the H-E
center exist, especially in the negative charge state.
8.2.1 Possible Configurations of the Negatively Charged Hydroxyl-E Center
Center
Figure 8.1: Possible configurations of an H atom interacting with the a- structure for the positive neutral and negative charge state.
An H
always tends to attach to a bridging O (top).
For the neutral charge state there are three possibilities (middle), from left to right: The H atom becomes interstitial, the H atom causes one of the O-Si bonds to break, forming a new H-E
center or the H atom remains attached. The latter is only possible when the H can transfer its
electron to an electron-accepting site nearby.
When negatively charged, there are even four possible outcomes (bottom). From left to right: The H sticks to a Si atom, a negatively charged H-E
is formed or the H atom remains attached. This is, again, only possible if a feature capable of
hosting two electrons is present nearby. Finally, there is a configuration with a hydroxyl group, but showing a bond between the two Si atoms. This bond resembles an OV, which is why this configuration will be referred to as OV-like.
The colored symbols in the bottom left corner of each figure relate this figure to the following Fig. 8.2 in which the same symbols and colors are used for the respective configurations. The shape indicates the
charge state and the colors signal similarity: The H-E
configurations are kept in blue and the stick configurations in green.
As already observed for the neutral charge state, the H-E shows various configurations when negatively charged. In general, one can distinguish
between four configurations (see Fig. 8.1):
-
• The H binds to a silicon (Si) atom, which makes the Si atom five-coordinated (see Fig. 8.1 violet triangle).
-
• There is a negatively charged version of the H-E
center. In many, but not all of these configurations the hydroxyl group is arranged so that it points towards the Si atom with the broken bond, a configuration that was never seen for the positive or neutral charged counterparts within the scope of this work (see Fig. 8.1 blue triangle).
-
• The H can stick to the O atom without breaking one of the bonds, similar to the neutral charge state referred to as stick in Chapter 5. This is only possible if a different feature capable of capturing both electrons is present nearby in the structure. This could be, for example, a Si with wide O–Si–O bond angle (see Fig. 8.1 green triangle).
-
• The fourth configuration encountered will be referred to as oxygen-vacancy like (OV-like) in the following. This is due to the wave function being preferably located between the two involved Si atoms, considerably reducing their distance and resembling a Si–Si bond as in an OV (see Fig. 8.1 yellow triangle).
However, it will be shown in the following that the only important configuration in the negative charge state is the H Atom bound to the Si atom since this configuration seems to have far lower energies than the other three options.
8.2.2 Myriads of Local Minima on the Potential Energy Surfaces
In [113] it is stated that the number of local minima on a PES grows exponentially with the number of atoms considered. This poses the question of how to properly interpret the configurations obtained by using rather simple steepest-descent methods, as it is done in
our DFT geometric optimization calculations. Such a method is not able to determine a global minimum, but only a local one, also critically dependent on the initial guess. Therefore, it was recently suggested to use a Monte-Carlo assisted geometric optimization
algorithm instead. The respective algorithm, which is currently under development, creates the different defect types introduced in Fig. 8.1 by
targeted distortion of the defect-free structure. Thereby different starting points (seeds) are created. The subsequent geometric optimization leads to many different configurations, which all converge into different local minima. Two example results are shown in Fig. 8.2. Here it is clearly visible that the preferred negative state is with the H binding to a Si atom. For the neutral charge state, it seems as if there are clusters for the interstitial configuration and for the H-E at comparable energies. Which one is lower depends on the structure. Of course, this does not
hold any information about the barriers interlinking the different “states” identified in these plots. Therefore in a next step, these barriers should be calculated for a series of defects.
Figure 8.2: Scatter plots showing the energies obtained from a Monte-Carlo assisted geometric optimization of the defect types from Fig. 8.1 in two different structures.
Each point denotes the energy of a converged Monte-Carlo trajectory. The used symbols correspond to Fig. 8.1. Technically every point could correspond to one “state” in a multi-state model, however, note that the
points in these plots form clusters which often, but not always, can be associated with clusters of very similar geometric configurations. For example, consider the H-E center which can either form on the right or left Si atom. For such reflection symmetric defects
also the respective results are split into a right and a left column in the above figures. If within one cluster the geometric configurations are very similar, it can be treated as a “state” with the energy of the respective lowest point of the cluster.
Technically all of the points in these plots denote a local minimum. Henceforth, a multi-state model of such defects would actually have to include all these points and the respective barriers between them. Clearly, this is next to impossible to calculate. However, very often the optimization leads to geometrically (and energetically) very similar structures, which form the clusters in Fig. 8.2. Such a cluster can, therefore, be regarded as “state”, the respective energy of such a “state” would be the minimum energy of the cluster. However, it should be noted that not every cluster in this figure
automatically is a cluster of geometrically similar configurations. A simple distinction can be made for defects with a reflection symmetry. This is, for example, the H-E center for which the hydroxyl group can either bind to the right or the left Si atom. Such
symmetries are considered in Fig. 8.2 by two separate columns, forming possibly different “states”.
It is very well visible that for the positive and neutral charge state the involved defect types are the ones that were investigated throughout this thesis, further supporting the models discussed in this work. For the negatively charged state, it seems as if by far the preferred configuration is for the H to bind to a Si atom. If the minima of all important configurations lie at comparable energies (as in Fig. 8.2 (left)), this could lead to interesting reaction dynamics. For example, the Si-bound state could well give a new insight into the double-capture and emission processes. Also, its role as an additional volatile state cannot be ruled out. Of course, this is all highly dependent on the barriers between the different states.
Deeper Insight Using New Barrier Calculation Method
Unfortunately, the Monte-Carlo assisted defect search method alone does not provide any information on the barriers interlinking the different clusters. These barriers are partly purely thermally activated and partly NMP barriers (see Section 2.2). Currently a new promising approach is under development which also allows for a minimum search for NMP transitions. With this algorithm, the problem of the purely linear interpolation of the PESs as done in Chapter 7 can be overcome and it should be possible to calculate much more accurate NMP barriers. Recently the Monte Carlo assisted geometric optimization algorithm also was extended to be able to find puckered configurations as needed for the NMP four-state model. Using a combination of these two new methods should allow for even more insight into the H-related defects and H kinetics discussed in this thesis.
A The Energy Alignment Problem
Due to the inherent inaccuracy in DFT calculations and the limited size of the cells used, a few problems arise that will be discussed in the following. Especially the limited cell size in combination with the periodic boundary condition is responsible for possible self-interaction of an introduced defect since its long-range interaction is re-introduced to the cell by the periodic boundary conditions. This can lead to background charge effects and furthermore, one also has to be careful to define a reliable energy reference the calculated energies can be compared to. The defect calculation is traditionally approached via the formation energy in a neutral host material:
Here is the energy of the
simulated supercell containing the defect whereas
is the defect-free bulk
structure which is used as a reference.
denotes the number of atoms of species
added (or removed) to create the defect, and the corresponding atomic chemical potential
.
For charged defects, the situation is more complicated, since the formation energy cannot be referenced to the neutral bulk reference anymore, therefore a chemical potential for the electrons has to be introduced [229, 230]. An equation for the formation energy of
charged structures, however, has to take into account that electrons are exchanged with the Fermi level. The Fermi level is referenced with respect to the valence-band
maximum in the bulk, in other words,
at the top of the valence band (
) of the bulk structure. For a structure with
charge
this yields:
is the Fermi level, referenced to the
valence-band maximum in the bulk. Due to the choice of this reference, the energy of the bulk valence-band maximum,
appears in the equation for formation energies of
charged states. The alignment necessary to compare PESs of different charge state then is nothing more than their differences in formation energy. To give an example, the trap level
for a positive and a neutral structure can be
determined by the difference in formation energy:
which is just the subtraction of eq. (A.2) - (A.1). This simple alignment scheme was used to calculate most of the transitions throughout this work. It does, however, suffer from some shortcomings, therefore possible errors shall be discussed in this section. Comparing energies of DFT calculations carried out in different cells (possibly also different cell sizes) or for different charge states are affected by considerable uncertainties. The main corrections that should be considered are:
-
• Potential alignment relative to a defect-free structure;
-
• Image charge correction (especially for charged defects);
-
• Band-gap alignment - the size of the calculated band-gap in DFT is typically smaller than the experimentally measured one.
These are discussed in several publications [229, 231–235]. In the following, the findings and their implication for this work are discussed.
A.1 Potential Alignment
The found for the bulk (i.e. in a defect-free
supercell) cannot be directly compared to the supercell containing a defect, for a number of reasons. An important one is the referencing of
, which is different across the various DFT
codes. Depending on the referencing method, any deviation from the bulk case can lead to
not converging to its bulk value far away from
the introduced defect [229, 232]. In the CP2K code, which was used throughout this thesis,
is referenced to the average of the potential over the whole unit cell [150]. The misalignment can be estimated by comparing the electrostatic potential in the “true” bulk structure to the potential in the region of the neutral defective structure far away
from the defect. The electronic structure in this region should be very similar to the bulk, except for the background charge shift introduced by the defect. Therefore, the alignment yields:
It is evident that the use of large supercells weakens this effect considerably [234] and as shown in [232] (albeit for different materials) the correction already is fairly low for supercells of 216 atoms (as used for the vast majority of the structures in this work).
A.2 Image Charge Correction
Like the potential mismatch, this effect also originates in the periodic boundary conditions. Even when using very large supercells with only one defect this still corresponds to extremely high and unphysical defect concentrations in semiconductors. When using periodic boundary conditions, charge neutrality must be ensured within a supercell, thus a homogeneous compensating background charge is introduced in those calculations. This background charge, however, has no equivalent in the real oxide since defect densities there are smaller by orders of magnitude. The image charge correction corrects for the charge interaction with the homogenous background charge and with its periodic image (originating from the boundary conditions). For the ideal case of a point charge the correction energy can be calculated as
where is the charge,
is the side length of the supercell and
the Madelung constant [236] which are different for each unit cell. Note that when neutrally charged, this correction term disappears. Therefore, also a second order term is considered:
Correction schemes all comprise but differ in estimating
[234]. The most popular schemes are:
-
• Markov-Payne correction scheme [237], considering the interaction of the localized charge density with a uniform compensating background charge. The main problem is that there is no clear definition for calculating the localized charge density. Furthermore, both densities involve integration over the charge densities making it computationally demanding.
-
• Freysolt-Neubauer-Van de Walle (FNV) correction scheme [235], which is an approach combining the above-discussed problem of the potential mismatch and the image charge correction at once by using the defect-free structure (instead of the neutral structure with defect) for calculating the reference energy [233, 234].
-
• Lany-Zunger correction scheme [232], which calculates
directly from the total charge difference between the charge densities of the neutral and the charged calculation using a delocalized screening charge density as a simplification. It is most likely the simplest one of the presented schemes, since an analytic form can be found, which does not need integration over the charge density as in the other corrections [234]. It, therefore, was applied in [79] and Chapter 4.
The mentioned corrections primarily affect transitions between states of different charge, therefore the results in Chapter 4 (for which a Lany-Zunger correction was applied), and partly also Chapter 7. An estimation based on [79] yields a correction on the order of 0.1 eV (in agreement with [234]) and, therefore, most likely on the same order of magnitude as possible other errors made in the calculations if the global minimum is missed by the geometric optimization or by the assumption of linear interpolation in Chapter 7. This could very well have an impact on some of the results presented in this work. However, it should be noted that the main results in this work rely on calculations of transitions within the same charge state. Those transitions discussed in Chapters 5 and 6 would, in any case, only be very weakly affected by such corrections.
A.3 Band-Gap Correction
Most of the DFT functionals tend to underestimate the bang-gap [79, 231, 238, 239]. However, the usage of hybrid functionals has improved the situation considerably. Whereas the underestimation of the band-gap was as high as 40% when using LDA or GGA functionals [238] it has dropped to less than 10% for the PBE0 TC LRC [79]. In [240] it is shown that the correction schemes do not represent a universal cure for the problem. Three different correction variants are presented, depending on the energies of the single-particle defect levels relative to the band edges. In the most complicated case, the correction scheme can lead to cases where defects, which lay outside of the band-gap, are shifted to lie inside after correction. The needed correction can vary between different charge states of the same defect.
Naturally, the best way to avoid large uncertainties in the band-gap correction is to use functionals that already provide an accurate band-gap, which is also the path chosen in this work. The best
band-gaps can be achieved by using a self-consistent LDA+U method [241]. However, as mentioned above, for the PBE0 TC LRC hybrid functionals [97] the band-gap-error is only 0.8 eV or only
10% [79]. A band-gap correction was therefore disregarded since the uncertainty introduced
by such a correction possibly would lie within the same order of magnitude as the already low error when using this functional.
A.4 Device Band Structure and NMP Model
At material interfaces such as the semiconductor-oxide interface in MOS devices, the band structure abruptly changes leading to energetic barriers for the carrier gas. It is common to draw the local band edges (conduction and valence band edge) as a function of
position. These so-called band diagrams are a popular method of illustrating processes in semiconductor devices. In this thesis, we only deal with fictive silicon (Si) devices with amorphous silicon dioxide (a-) oxide. When also considering a poly-Si gate the band
diagram looks as depicted in Fig. A.1. The poly-Si gate, however, is only shown for completeness. Capture or emission from/to the gate is not considered in this work.
Figure A.1: In a band diagram, the local values of the conduction and valence band edges are drawn as a function of position. At a material boundary, the band edges abruptly change, giving rise to energetic barriers or wells. The shown band diagram corresponds to the situation in the fictitious Si-based MOS structure used in this work.
A.4.1 Energy Alignment of PESs of Different Charge
In order to be able to meaningfully compare the DFT-energies of different charge states, it is necessary to align them using a common reference point. A reliable reference point, for instance, could be a very deep Kohn-Sham level (see Section 2.1), that is practically independent of the different charge. The deep Kohn-Sham levels are assumed to be the same states across both charge states and uninfluenced by the additional charge. However, calculating the deep Kohn-sham levels is computationally very expensive in DFT, moreover when using pseudopotentials these levels are explicitly avoided, due to the very reason that they are not considerably altered.
A different approach is to take the highest occupied state of the neutral and defect-free structure as a reference point. Per definition, this state is the valence band edge in this structure. If a defect is
introduced into the structure all the defect energy levels are referred to the previously defined valence band edge. This referencing system was used throughout this work. Furthermore, it has to be taken into account that when a hole is emitted (captured) in this
model, it gains (looses) the band-offset energy (see Fig. A.1 and Fig. A.2). When referencing to the highest occupied state (valence band edge) of the
defect-free neutral structure the alignment becomes:
where in our case q (see also eq. (A.3)). This alignment was used throughout this work whenever PESs of different charge states were involved.
A.4.2 Shift Due to Interaction with an Electric Field
Figure A.2: Linked representations using PESs like Fig. 2.4 and the MOSFET band structure
as in Fig. A.1, and their dependence on the electric field according to eq. (2.35). In the classical considerations, the substrate holes initially lie at the valence
band. An electric field decays linearly along the oxide changing the band structure (right), thereby also shifting the energy levels relative to each other relative to the case when no field is applied (left). Note that due to the work function difference also in the field-free case there is a little band bending also when no field is applied (left). The difference -
is typically referred to as the thermodynamic trap level
. Note that in the hole-picture the minimum of
is assumed
as a reference, fixed at the valence band edge (
) and therefore
(see Section 4.3.2).
In a simple (first-order) model the shift of the PES of the charged state depends linearly on the applied electric field (eq. (2.35)). Fig. A.2 shows how the PESs in NMP theory are interlinked with the defect levels in a band diagram scheme as Fig. A.1. As can be seen in Fig. A.2 the energetic barriers encountered in a model which considers only the electronic energies of the defect to describe a hole capture process are always lower or at least equal to the barriers in NMP theory, the
difference being in Fig. A.2. The two figures also illustrate the model used in this work when calculating capture or emission times of defects. In this model the
Si/
band offset (
) is set to 4.5 eV and the defect sits in the
but captures and emits its charge from/to the Si
conduction or valence band respectively. This model has been used to study oxygen defect behavior in previous publications [3, 46, 55, 132, 242]. All calculations using this model in this work assume a semiclassical approach based on [105] and [103]. Thereby, the
transition barriers
are always calculated in their classical limit (see Section
2.2.1).
B The Weibull Distribution
The Weibull distribution (WBD) is a continuous probability distribution named after Swedish mathematician Waloddi Weibull. Although the publication dates from 1951 [186] the distribution had been previously described by Frechet [243] and used to describe the distribution of particle sizes [244]. The WBD has a very broad applicability [187, 188] and is also widely used in reliability engineering [39, 245, 246]. The probability distribution function of a Weibull distributed random variable is defined as [247]:
with the shape parameters and the scale parameter
. The corresponding cumulative distribution function is
given as:
The estimation value and variance
are:
where is the Gamma-function
The influence of the parameters and
on the probability distribution function
is shown in Fig. B.1. Note that the characteristics are completely different for distributions with
and
. For
the Weibull distribution becomes an exponential distribution with the characteristic
parameter
[247]. For a value of
3.6 the WBD becomes a symmetric function resembling a normal distribution
[248].
Figure B.1: Weibull distributions for different values of the shape parameter and scale parameter
. The behavior is very different for values of
and
. For
the Weibull distribution becomes an exponential distribution with the characteristic param-
eter
[247]. For a value of
3.6 (see purple line left) the WBD becomes a symmetric function resembling a nor-
mal distribution [248].
Bibliography
-
[1] K.S. Ralls, W.J. Skocpol, L.D. Jackel, R.E. Howard, L.A. Fetter, R.W. Epworth, and D.M. Tennant. “Discrete Resistance Switching in Submicrometer Silicon Inversion Layers: Individual Interface Traps and Low-Frequency (1/f) Noise”. In: Physical Review Letters 52.3 (1984), pp. 228–231.
-
[2] M.J. Kirton and M.J. Uren. “Noise in Solid-State Microstructures: A New Perspective on Individual Defects, Interface States and Low-Frequency (1/f) Noise”. In: Advances in Physics 38.4 (1989), pp. 367–486.
-
[3] T. Grasser. “Stochastic Charge Trapping in Oxides: From Random Telegraph Noise to Bias Temperature Instabilities”. In: Microelectronics Reliability 52 (2012). (invited), pp. 39–70.
-
[4] K.O. Jeppson and C.M. Svensson. “Negative Bias Stress of MOS Devices at High Electric Fields and Degradation of MNOS Devices”. In: Journal of Applied Physics 48.5 (1977), pp. 2004–2014.
-
[5] S. Ogawa and N. Shiono. “Generalized Diffusion-Reaction Model for the Low-Field Charge Build Up Instability at the Si/SiO2 Interface”. In: Physical Review B 51.7 (1995), pp. 4218–4230.
-
[6] T. Grasser, B. Kaczer, W. Gös, T. Aichinger, P. Hehenberger, and M. Nelhiebel. “A Two-Stage Model for Negative Bias Temperature Instability”. In: Proceedings of the International Reliability Physics Symposium (IRPS). 2009, pp. 33–44.
-
[7] T. Grasser. “The Capture/Emission Time Map Approach to the Bias Temperature Instability”. In: Bias Temperature Instability for Devices and Circuits. Ed. by T. Grasser. Springer, New York, 2014, pp. 447–484.
-
[8] J.P. Campbell, J. Qin, K.P. Cheung, L.C. Yu, J.S. Suehle, A. Oates, and K. Sheng. “Random Telegraph Noise in Highly Scales nMOSFETs”. In: Proceedings of the International Reliability Physics Symposium (IRPS). 2009, pp. 382–388.
-
[9] D.M. Fleetwood. “Energies and microstructures of defects contributing to 1/f noise in microelectronic materials and devices”. In: International Conference on Noise and Fluctuations (ICNF). IEEE. 2015, pp. 1–6.
-
[10] S. Rauch and G.L. Rosa. “CMOS hot carrier: From physics to end of life projections, and qualification”. In: 2010.
-
[11] A. Bravaix and V. Huard. “Hot-carrier degradation issues in advanced CMOS nodes”. In: Proceedings of the European Symposium on Reliability of Electron Devices, Failure Physics and Analysis (ESREF). tutorial. 2010, pp. 1267–1272.
-
[12] A. Acovic, G. La Rosa, and Y.-C. Sun. “A review of hot-carrier degradation mechanisms in MOSFETs”. In: Microelectronics Reliability 36.7-8 (1996), pp. 845–869.
-
[13] T. Grasser, ed. Hot Carrier Degradation in Semiconductor Devices. Springer International Publishing, 2014. isbn: 978-3-319-08993-5.
-
[14] A. Ghetti. “Gate oxide reliability: Physical and computational models”. In: Predictive Simulation of Semiconductor Processing. Springer, 2004, pp. 201–258.
-
[15] K.F. Schuegraf and C. Hu. “Hole Injection SiO2 Breakdown Model for Very Low Voltage Lifetime Extrapolation”. In: IEEE Transactions on Electron Devices 41.5 (1994), pp. 761–767.
-
[16] J.P. Campbell, P.M. Lenahan, C.J. Cochrane, A.T. Krishnan, and S. Krishnan. “Atomic-Scale Defects Involved in the Negative-Bias Temperature Instability”. In: IEEE Transactions on Device and Materials Reliability 7.4 (2007), pp. 540–557.
-
[17] M. Houssa, V.V. Afanas’ev, A. Stesmans, M. Aoulaiche, G. Groeseneken, and M.M. Heyns. “Insights on the Physical Mechanism behind Negative Bias Temperature Instabilities”. In: Applied Physics Letters 90.4 (2007), p. 043505.
-
[18] T. Grasser, H. Reisinger, P.-J. Wagner, W. Gös, F. Schanovsky, and B. Kaczer. “The Time Dependent Defect Spectroscopy (TDDS) for the Characterization of the Bias Temperature Instability”. In: Proceedings of the International Reliability Physics Symposium (IRPS). 2010, pp. 16–25.
-
[19] C.A. Mack. “Fifty years of Moore’s law”. In: IEEE Transactions on Semiconductor Manufacturing 24.2 (2011), pp. 202–207.
-
[20] T. Nagumo, K. Takeuchi, S. Yokogawa, K. Imai, and Y. Hayashi. “New Analysis Methods for Comprehensive Understanding of Random Telegraph Noise”. In: Proceedings of the International Electron Devices Meeting (IEDM). 2009, pp. 759–762.
-
[21] D.K. Schroder. “Electrical Characterization of Defects”. In: Defects in Microelectronic Materials and Devices. Ed. by D.M. Fleetwood, S.T. Pantelides, and R.D. Scrimpf. CRC Press, 2009, pp. 120–163.
-
[22] J. Franco, B. Kaczer, M. Toledano-Luque, P.J. Roussel, J. Mitard, L.A. Ragnarsson, L. Witters, T. Chiarella, M. Togo, N. Horiguchi, G. Groeseneken, M.F. Bukhori, T. Grasser, and A. Asenov. “Impact of Single Charged Gate Oxide Defects on the Performance and Scaling of Nanoscaled FETs”. In: Proceedings of the International Reliability Physics Symposium (IRPS). 2012, 5A.4.1.
-
[23] B. Kaczer, T. Grasser, J. Martin-Martinez, E. Simoen, M. Aoulaiche, P.J. Roussel, and G. Groeseneken. “NBTI from the Perspective of Defect States with Widely Distributed Time Scales”. In: Proceedings of the International Reliability Physics Symposium (IRPS). 2009, pp. 55–60.
-
[24] H. Reisinger, T. Grasser, and C. Schlünder. “A Study of NBTI by the Statistical Analysis of the Properties of Individual Defects in pMOSFETs”. In: Proceedings of the International Integrated Reliability Workshop (IIRW). 2009, pp. 30–35.
-
[25] B. Kaczer, T. Grasser, P.J. Roussel, J. Franco, R. Degraeve, L.A. Ragnarsson, E. Simoen, G. Groeseneken, and H. Reisinger. “Origin of NBTI Variability in Deeply Scaled PFETs”. In: Proceedings of the International Reliability Physics Symposium (IRPS). 2010, pp. 26–32.
-
[26] D.K. Schroder. “Negative Bias Temperature Instability: What Do We Understand?” In: Microelectronics Reliability 47.6 (2007), pp. 841–852.
-
[27] D.K. Schroder and J.A. Babcock. “Negative Bias Temperature Instability: Road to Cross in Deep Submicron Silicon Semiconductor Manufacturing”. In: Journal of Applied Physics 94.1 (2003), pp. 1–18.
-
[28] T. Grasser, ed. Bias Temperature Instability for Devices and Circuits. Springer Science+Business Media New York, 2013. isbn: 978-1-4614-7908-6.
-
[29] G. La Rosa, F. Guarin, S. Rauch, A. Acovic, J. Lukaitis, and E. Crabbe. “NBTI-channel hot carrier effects in PMOSFETs in advanced CMOS technologies”. In: Proceedings of the International Reliability Physics Symposium (IRPS). IEEE. 1997, pp. 282–286.
-
[30] C. Schlünder, R. Brederlow, B. Ankele, W. Gustin, K. Goser, and R. Thewes. “Effects of Inhomogeneous Negative Bias Temperature Stress on p-channel MOSFETs of Analog and RF Circuits”. In: Microelectronics Reliability 45.1 (2005), pp. 39–46.
-
[31] M.-C. Wang, Z.-Y. Hsieh, S.-Y. Chen, and H.-S. Huang. “Investigation of Contribution Ratio between NBTI and HC Effects in PMOSFETs under Deep-Submicron Process”. In: 2007 First International Conference on Integration and Commercialization of Micro and Nanosystems. American Society of Mechanical Engineers. 2007, pp. 299–304.
-
[32] C. Schlünder, S. Aresu, G. Georgakos, W. Kanert, H. Reisinger, K. Hofmann, and W. Gustin. “HCI vs. BTI?-Neither one’s out”. In: Proceedings of the International Reliability Physics Symposium (IRPS). IEEE. 2012, 2F–4.
-
[33] G. Rott, K. Rott, H. Reisinger, W. Gustin, and T. Grasser. “Mixture of negative bias temperature instability and hot-carrier driven threshold voltage degradation of 130nm technology p-channel transistors”. In: Microelectronics Reliability 54.9 (2014), pp. 2310–2314.
-
[34] B. Kaczer, J. Franco, S.E. Tyaginov, M. Jech, G. Rzepa, T. Grasser, B.J. O’Sullivan, R. Ritzenhaler, T. Schram, A. Spessot, D. Linten, and N. Horiguchi. “Mapping of CMOS FET Degradation in Bias Space–Application to Dram Peripheral Devices”. In: Journal of Vacuum Science & Technology B 35.1 (2017), 01A109-1–01A109-6.
-
[35] B. Ullmann, M. Jech, S.E. Tyaginov, M. Waltl, Y. Illarionov, A. Grill, K. Puschkarsky, H. Reisinger, and T. Grasser. “The Impact of Mixed Negative Bias Temperature Instability and Hot Carrier Stress on Single Oxide Defects”. In: Proceedings of the International Reliability Physics Symposium (IRPS). 2017, XT-10.1–XT-10.6. isbn: 978-1-5090-6642-1.
-
[36] M. Waltl. “Experimental Characterization of Bias Temperature Instabilities in Modern Transistor Technologies”. Dissertation. 2016.
-
[37] T.L. Tewksbury. “Relaxation Effects in MOS Devices due to Tunnel Exchange with Near-Interface Oxide Traps”. Ph.D. Thesis. MIT, 1992.
-
[38] G. Rzepa. “Microscopic Modeling of NBTI in MOS Transistors”. MA thesis. TU Wien, E360, 2013.
-
[39] B. Kaczer, P. Roussel, T. Grasser, and G. Groeseneken. “Statistics of Multiple Trapped Charges in the Gate Oxide of Deeply Scaled MOSFET Devices-Application to NBTI”. In: IEEE Electron Device Letters 31.5 (2010), pp. 411–413.
-
[40] V. Huard, M. Denais, and C. Parthasarathy. “NBTI Degradation: From Physical Mechanisms to Modelling”. In: Microelectronics Reliability 46.1 (2006), pp. 1–23.
-
[41] J.P. Campbell, P.M. Lenahan, A.T. Krishnan, and S. Krishnan. “Density of States and Structure of NBTI-Induced Defects in Plasma-Nitrided pMOSFETs”. In: Proceedings of the International Reliability Physics Symposium (IRPS). 2007, pp. 503–510.
-
[42] A. Kerber, E. Cartier, L. Pantisano, R. Degraeve, T. Kauerauf, Y. Kim, A. Hou, G. Groeseneken, H.E. Maes, and U. Schwalke. “Origin of the threshold voltage instability in SiO2 /HfO2 dual layer gate dielectrics”. In: IEEE Electron Device Letters 24.2 (2003), pp. 87–89.
-
[43] T. Grasser, K. Rott, H. Reisinger, M. Waltl, J. Franco, and B. Kaczer. “A Unified Perspective of RTN and BTI”. In: Proceedings of the International Reliability Physics Symposium (IRPS). 2014, 4A.5.1–4A.5.7.
-
[44] T. Grasser, H. Reisinger, P.-J. Wagner, and B. Kaczer. “The Time Dependent Defect Spectroscopy for the Characterization of Border Traps in Metal-Oxide-Semiconductor Transistors”. In: Physical Review B 82.24 (2010), p. 245318.
-
[45] A. Karwath and M. Schulz. “Deep Level Transient Spectroscopy on Single, Isolated Interface Traps in Field-Effect Transistors”. In: Applied Physics Letters 52.8 (1988), pp. 634–636.
-
[46] T. Grasser, B. Kaczer, W. Gös, H. Reisinger, T. Aichinger, P. Hehenberger, P.-J. Wagner, F. Schanovsky, J. Franco, M. Toledano-Luque, and M. Nelhiebel. “The Paradigm Shift in Understanding the Bias Temperature Instability: From Reaction-Diffusion to Switching Oxide Traps”. In: IEEE Transactions on Electron Devices 58.11 (2011), pp. 3652–3666.
-
[47] A. Asenov, R. Balasubramaniam, A.R. Brown, and J.H. Davies. “RTS Amplitudes in Decananometer MOSFETs: 3-D Simulation Study”. In: IEEE Transactions on Electron Devices 50.3 (2003), pp. 839–845.
-
[48] V. Huard, C. Parthasarathy, and M. Denais. “Single-Hole Detrapping Events in pMOSFETs NBTI Degradation”. In: Proceedings of the International Integrated Reliability Workshop (IIRW). 2005, pp. 5–9.
-
[49] T. Grasser, H. Reisinger, W. Gös, T. Aichinger, P. Hehenberger, P.-J. Wagner, M. Nelhiebel, J. Franco, and B. Kaczer. “Switching Oxide Traps as the Missing Link between Negative Bias Temperature Instability and Random Telegraph Noise”. In: Proceedings of the International Electron Devices Meeting (IEDM). 2009, pp. 729–732.
-
[50] H. Reisinger, T. Grasser, W. Gustin, and C. Schlünder. “The Statistical Analysis of Individual Defects Constituting NBTI and its Implications for Modeling DC- and AC-Stress”. In: Proceedings of the International Reliability Physics Symposium (IRPS). 2010, pp. 7–15.
-
[51] M. Waltl, W. Gös, K. Rott, H. Reisinger, and T. Grasser. “A Single-Trap Study of PBTI in SiON nMOS Transistors: Similarities and Differences to the NBTI/pMOS Case”. In: Proceedings of the International Reliability Physics Symposium (IRPS). 2014, XT18.1.
-
[52] M. Toledano-Luque, B. Kaczer, P.J. Roussel, M.J. Cho, T. Grasser, and G. Groeseneken. “Temperature Dependence of the Emission and Capture Times of SiON Individual Traps after Positive Bias Temperature Stress”. In: Proceedings of the Workshop on Dielectrics in Microelectronics (WoDiM). 2010, pp. 1–2.
-
[53] K. Zhao, J.H. Stathis, B.P. Linder, E. Cartier, and A. Kerber. “PBTI Under Dynamic Stress: From a Single Defect Point of View”. In: Proceedings of the International Reliability Physics Symposium (IRPS). 2011, pp. 372–380.
-
[54] T. Grasser, H. Reisinger, K. Rott, M. Toledano-Luque, and B. Kaczer. “On the Microscopic Origin of the Frequency Dependence of Hole Trapping in pMOSFETs”. In: Proceedings of the International Electron Devices Meeting (IEDM). 2012, pp. 19.6.1–19.6.4.
-
[55] W. Gös, F. Schanovsky, H. Reisinger, B. Kaczer, and T. Grasser. “Bistable Defects as the Cause for NBTI and RTN”. In: Solid State Phenomena 178-179 (2011). (invited), pp. 473–482.
-
[56] F. Schanovsky, W. Gös, and T. Grasser. “A Detailed Evaluation of Model Defects as Candidates for the Bias Temperature Instability”. In: Proceedings of the International Conference on Simulation of Semiconductor Processes and Devices (SISPAD). 2013, pp. 1–4.
-
[57] T. Grasser, B. Kaczer, P. Hehenberger, W. Gös, R. O’Connor, H. Reisinger, W. Gustin, and C. Schlünder. “Simultaneous Extraction of Recoverable and Permanent Components Contributing to Bias-Temperature Instability”. In: Proceedings of the International Electron Devices Meeting (IEDM). 2007, pp. 801–804.
-
[58] T. Grasser and B. Kaczer. “Evidence that Two Tightly Coupled Mechanism are Responsible for Negative Bias Temperature Instability in Oxynitride MOSFETs”. In: IEEE Transactions on Electron Devices 56.5 (2009), pp. 1056–1062.
-
[59] V. Huard. “Two Independent Components Modeling for Negative Bias Temperature Instability”. In: Proceedings of the International Reliability Physics Symposium (IRPS). 2010, pp. 33–42.
-
[60] T. Grasser, T. Aichinger, H. Reisinger, J. Franco, P.-J. Wagner, M. Nelhiebel, C. Ortolland, and B. Kaczer. “On the ‘Permanent’ Component of NBTI”. In: Proceedings of the International Integrated Reliability Workshop (IIRW). 2010.
-
[61] A.A. Katsetos. “Negative Bias Temperature Instability (NBTI) Recovery with Bake”. In: Microelectronics Reliability 48.10 (2008), pp. 1655–1659.
-
[62] C. Benard, G. Math, P. Fornara, J. Ogier, and D. Goguenheim. “Influence of Various Process Steps on the Reliability of PMOSFETs Submitted to Negative Bias Temperature Instabilities”. In: Microelectronics Reliability 49 (2009), pp. 1008–1012.
-
[63] G. Pobegen, T. Aichinger, M. Nelhiebel, and T. Grasser. “Understanding Temperature Acceleration for NBTI”. In: Proceedings of the International Electron Devices Meeting (IEDM). 2011, pp. 27.3.1–27.3.4.
-
[64] G. Pobegen and T. Grasser. “On the Distribution of NBTI Time Constants on a Long, Temperature-Accelerated Time Scale”. In: IEEE Transactions on Electron Devices 60.7 (2013), pp. 2148–2155.
-
[65] Y. Yonamoto. “Generation/recovery mechanism of defects responsible for the permanent component in negative bias temperature instability”. In: Journal of Applied Physics 113.15 (2013), p. 154501.
-
[66] M. Uren, M.J. Kirton, and S. Collins. “Anomalous Telegraph Noise in Small-Area Silicon Metal-Oxide-Semiconductor Field-Effect Transistors”. In: Physical Review B 37.14 (1988), pp. 8346–8350.
-
[67] T. Grasser, K. Rott, H. Reisinger, M. Waltl, P.-J. Wagner, F. Schanovsky, W. Gös, G. Pobegen, and B. Kaczer. “Hydrogen-Related Volatile Defects as the Possible Cause for the Recoverable Component of NBTI”. In: Proceedings of the International Electron Devices Meeting (IEDM). 2013.
-
[68] T. Grasser, K. Rott, H. Reisinger, M. Waltl, and W. Gös. “Evidence for defect pairs in SiON pMOSFETs”. In: Proceedings of the International Symposium on Physical and Failure Analysis of Integrated Circuits (IPFA). IEEE. 2014, pp. 258–263.
-
[69] G. Rzepa, W. Gös, G. Rott, K. Rott, M. Karner, C. Kernstock, B. Kaczer, H. Reisinger, and T. Grasser. “Physical Modeling of NBTI: From Individual Defects to Devices”. In: Proceedings of the International Conference on Simulation of Semiconductor Processes and Devices (SISPAD). 2014, pp. 81–84.
-
[70] T. Grasser, M. Waltl, K. Puschkarsky, B. Stampfer, G. Rzepa, G. Pobegen, H. Reisinger, H. Arimura, and B. Kaczer. “Implications of Gate-Sided Hydrogen Release for Post-Stress Degradation Build-Up after BTI Stress”. In: 2017, 6A-2.1–6A-2.6.
-
[71] P. Hohenberg and W. Kohn. “Inhomogeneous Electron Gas”. In: Physical Review 136 (1964), B864.
-
[72] W. Kohn and L.J. Sham. “Self-consistent equations including exchange and correlation effects”. In: Physical Review 140 (1965), A1133.
-
[73] Foresman, J.B. and Frisch Æ. “Density Functional Theory”. In: Exploring Chemistry with Electronic Structure Methods. Gaussian, Inc, 1996, pp. 272–283.
-
[74] F. Herman, J.P. Van Dyke, and I.B. Ortenburger. “Improved statistical exchange approximation for inhomogeneous many-electron systems”. In: Physical Review Letters 22.16 (1969), p. 807.
-
[75] P.-S. Svendsen and U. von Barth. “Gradient expansion of the exchange energy from second-order density response theory”. In: Physical Review B 54.24 (1996), p. 17402.
-
[76] J.P. Perdew, K. Burke, and M. Ernzerhof. “Generalized gradient approximation made simple”. In: Physical Review Letters 77.18 (1996), p. 3865.
-
[77] R.M. Martin. “Basic theory and practical methods”. In: Electronic structure. Cambridge university press, 2004.
-
[78] R.M. Nieminen. “Supercell methods for defect calculations”. In: Theory of Defects in Semiconductors. Springer, 2007, pp. 29–68.
-
[79] A.-M. El-Sayed. “Atomistic Modelling of Charge Trapping Defects in Silicon Dioxide”. Ph.D. Thesis. University College London, 2015.
-
[80] K. Lejaeghere, G. Bihlmayer, T. Björkman, P. Blaha, S. Blügel, V. Blum, D. Caliste, I.E. Castelli, S.J. Clark, A. Dal Corso, et al. “Reproducibility in density functional theory calculations of solids”. In: Science 351.6280 (2016), aad3000.
-
[81] J. Hutter, M. Iannuzzi, F. Schiffmann, and J. VandeVondele. “CP2K: atomistic simulations of condensed matter systems”. In: Wiley Interdisciplinary Reviews: Computational Molecular Science 4.1 (2014), pp. 15–25.
-
[82] CP2K Manual. https://manual.cp2k.org/. Accessed: 2017-06-01.
-
[83] M.J. Frisch, G.W. Trucks, H.B. Schlegel, G.E. Scuseria, M.A. Robb, J.R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G.A. Petersson, et al. “Gaussian 09, Revision A. 02, Gaussian”. In: Inc., Wallingford, CT 200 (2009).
-
[84] J.M. Turney, A.C. Simmonett, R.M. Parrish, E.G. Hohenstein, F.A. Evangelista, J.T. Fermann, B.J. Mintz, L.A. Burns, J.J. Wilke, M.L. Abrams, et al. “Psi4: an open-source ab initio electronic structure program”. In: Wiley Interdisciplinary Reviews: Computational Molecular Science 2.4 (2012), pp. 556–565.
-
[85] G. Kresse and J. Furthmüller. “Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set”. In: Physical Review B 54.16 (1996), p. 11169.
-
[86] P. Blaha, K. Schwarz, G.K.H. Madsen, D. Kvasnicka, and J. Luitz. “wien2k”. In: An augmented plane wave+ local orbitals program for calculating crystal properties (2001).
-
[87] P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G.L. Chiarotti, M. Cococcioni, I. Dabo, et al. “QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials”. In: Journal of Physics: Condensed Matter 21.39 (2009), p. 395502.
-
[88] G. Lippert, J. Hutter, and M. Parrinello. “A hybrid Gaussian and plane wave density functional scheme”. In: Molecular Physics 92.3 (1997), pp. 477–488.
-
[89] G. Lippert, J. Hutter, and M. Parrinello. “The Gaussian and augmented-plane-wave density functional method for ab initio molecular dynamics simulations”. In: Theoretical Chemistry Accounts 103.2 (1999), pp. 124–140.
-
[90] J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing, and J. Hutter. “Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach”. In: Computer Physics Communications 167.2 (2005), pp. 103–128.
-
[91] N. Troullier and J.L. Martins. “Efficient pseudopotentials for plane-wave calculations”. In: Physical Review B 43.3 (1991), p. 1993.
-
[92] J.P. Perdew. “Climbing the ladder of density functional approximations”. In: MRS bulletin 38.9 (2013), pp. 743–750.
-
[93] J.P. Perdew and M. Levy. “Physical content of the exact Kohn-Sham orbital energies: band gaps and derivative discontinuities”. In: Physical Review Letters 51.20 (1983), p. 1884.
-
[94] J.L. Gavartin and A.L. Shluger. “Periodic density functional plane wave calculations of triplet exciton in NaCl”. In: Radiation effects and defects in solids 155.1-4 (2001), pp. 311–315.
-
[95] R. Dovesi, R. Orlando, C. Roetti, C. Pisani, and V.R. Saunders. “The periodic Hartree-Fock method and its implementation in the Crystal code”. In: Physica Status Solidi B Basic Research 217.1 (2000), pp. 63–88.
-
[96] J. Heyd and G.E. Scuseria. “Efficient hybrid density functional calculations in solids: assessment of the Heyd–Scuseria–Ernzerhof screened Coulomb hybrid functional”. In: The Journal of Chemical Physics 121.3 (2004), pp. 1187–1192.
-
[97] M. Guidon, J. Hutter, and J. VandeVondele. “Robust Periodic Hartree-Fock Exchange for Large-Scale Simulations Using Gaussian Basis Sets”. In: Journal of Chemical Theory and Computation 5.11 (2009), pp. 3010–3021.
-
[98] M. Guidon, J. Hutter, and J. VandeVondele. “Auxiliary density matrix methods for hartree- fock exchange calculations”. In: Journal of Chemical Theory and Computation 6.8 (2010), pp. 2348–2364.
-
[99] M. Born and R. Oppenheimer. “Zur quantentheorie der molekeln”. In: Annalen der Physik 389.20 (1927), pp. 457–484.
-
[100] M. Born, K. Huang, and M. Lax. “Dynamical theory of crystal lattices”. In: American Journal of Physics 23.7 (1955), pp. 474–474.
-
[101] W. Gös, F. Schanovsky, and T. Grasser. “Advanced Modeling of Oxide Defects”. In: Bias temperature instability for devices and circuits. Springer Science & Business Media, 2013, pp. 449–446.
-
[102] L.D. Landau. “Zur theorie der energieubertragung. II”. In: Physics of the Soviet Union 2.2 (1932), pp. 46–51.
-
[103] F. Schanovsky. “Atomistic Modeling in the Context of the Bias Temperature Instability”. Dissertation. E360, 2013.
-
[104] K. Huang and A. Rhys. “Theory of Light Absorption and Non-Radiative Transitions in F-Centres”. In: Proceedings of the Royal Society A 204 (1950), pp. 406–423.
-
[105] C.H. Henry and D.V. Lang. “Nonradiative Capture and Recombination by Multiphonon Emission in GaAs and GaP”. In: Physical Review B 15.2 (1977), pp. 989–1016.
-
[106] A.M. Stoneham. Theory of defects in solids: electronic structure of defects in insulators and semiconductors. Oxford University Press, 2001.
-
[107] M. Lax. “The Franck-Condon Principle and Its Application to Crystals”. In: The Journal of Chemical Physics 20.11 (1952), pp. 1752–1760.
-
[108] K.V. Mikkelsen and M.A. Ratner. “Electron tunneling in solid-state electron-transfer reactions”. In: Chemical Reviews 87.1 (1987), pp. 113–153.
-
[109] T.H. Keil. “Shapes of impurity absorption bands in solids”. In: Physical Review 140.2A (1965), A601.
-
[110] E. Fermi. “Nuclear physics”. In: A course given by Enrico Fermi at the University of Chicago, 1949, Chicago: University of Chicago Press, 1950, Rev. ed.. Vol. 1. 1950.
-
[111] W.B. Fowler, J.K. Rudra, M.E. Zvanut, and F.J. Feigl. “Hysteresis and Franck-Condon relaxation in insulator-semiconductor tunneling”. In: Physical Review B 41.12 (1990), p. 8313.
-
[112] W. Gös, M. Toledano-Luque, O. Baumgartner, M. Bina, F. Schanovsky, B. Kaczer, and T. Grasser. “Understanding Correlated Drain and Gate Current Fluctuations”. In: Proceedings of the International Symposium on Physical and Failure Analysis of Integrated Circuits (IPFA). invited. 2013, pp. 51–56.
-
[113] C.J. Pickard and R.J. Needs. “Ab initio random structure searching”. In: Journal of Physics: Condensed Matter 23.5 (2011), p. 053201.
-
[114] A. Nitzan. “Chemical Reactions in Condensed Phases”. In: Chemical dynamics in condensed phases: relaxation, transfer and reactions in condensed molecular systems. Oxford University Press, 2006, pp. 483–535.
-
[115] A.F. Voter, F. Montalenti, and T.C. Germann. “Extending the time scale in atomistic simulation of materials”. In: Annual Review of Materials Research 32.1 (2002), pp. 321–346.
-
[116] S. Arrhenius. Über die Dissociationswärme und den Einfluss der Temperatur auf den Dissociationsgrad der Elektrolyte. Wilhelm Engelmann, 1889.
-
[117] K.A. Connors. Chemical kinetics: the study of reaction rates in solution. John Wiley & Sons, 1990.
-
[118] H. Jónsson, G. Mills, and K.W. Jacobsen. “Nudged elastic band method for finding minimum energy paths of transitions”. In: (1998).
-
[119] G. Kresse, M. Marsman, and J. Furthmuller. VASP manual. Universität Wien, Sensengasse 8, A-1130 Wien, Austria, 2009.
-
[120] K.R. Gillilan R.E.and Wilson. “Shadowing, rare events, and rubber bands. A variational Verlet algorithm for molecular dynamics”. In: The Journal of Chemical Physics 97.3 (1992), pp. 1757–1772.
-
[121] D. Sheppard, R. Terrell, and G. Henkelman. “Optimization methods for finding minimum energy paths”. In: The Journal of Chemical Physics 128.13 (2008), p. 134106.
-
[122] G. Henkelman, B.P. Uberuaga, and H. Jónsson. “A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths”. In: The Journal of Chemical Physics 113.22 (2000), pp. 9901–9904.
-
[123] A. Goetzberger and H.E. Nigh. “Surface Charge After Annealing of Al-SiO2 -Si Structures Under Bias”. In: Proceedings of the IEEE 54.10 (1966), pp. 1454–1454.
-
[124] Y. Miura and Y. Matukura. “Investigation of Silicon-Silicon Dioxide Interface Using MOS Structure”. In: Japanese Journal of Applied Physics 5 (1966), p. 180.
-
[125] V. Huard, C. Parthasarathy, N. Rallet, C. Guerin, M. Mammase, D. Barge, and C. Ouvrard. “New Characterization and Modeling Approach for NBTI Degradation from Transistor to Product Level”. In: Proceedings of the International Electron Devices Meeting (IEDM). 2007, pp. 797–800.
-
[126] I. Lundstrom and C. Svensson. “Tunneling to Traps in Insulators”. In: Journal of Applied Physics 43.12 (1972), pp. 5045–5047.
-
[127] F.P. Heiman and G. Warfield. “The Effects of Oxide Traps on the MOS Capacitance”. In: 12.4 (1965), pp. 167–178.
-
[128] S. Christensson, I. Lundström, and C. Svensson. “Low Frequency Noise in MOS Transistors – I Theory”. In: Solid-State Electronics 11 (1968), pp. 797–812.
-
[129] W. Shockley and W.T. Read. “Statistics of the Recombinations of Holes and Electrons”. In: Physical Review 87.5 (1952), pp. 835–842.
-
[130] A.L. McWhorter. “1/f Noise and Germanium Surface Properties”. In: Semiconductor Surface Physics (1957), pp. 207–228.
-
[131] M. Masuduzzaman, A.E. Islam, and M.A. Alam. “Exploring the Capability of Multifrequency Charge Pumping in Resolving Location and Energy Levels of Traps Within Dielectric”. In: IEEE Transactions on Electron Devices 55.12 (2008), pp. 3421–3431.
-
[132] W. Gös. “Hole Trapping and the Negative Bias Temperature Instability”. Dissertation. Technische Universität Wien, 2011.
-
[133] S. Guo, R. Wang, D. Mao, Y. Wang, and R. Huang. “Anomalous random telegraph noise in nanoscale transistors as direct evidence of two metastable states of oxide traps”. In: Scientific Reports 7 (2017).
-
[134] T. Grasser, K. Rott, H. Reisinger, P.-J. Wagner, W. Gös, F. Schanovsky, M. Waltl, M. Toledano-Luque, and B. Kaczer. “Advanced Characterization of Oxide Traps: The Dynamic Time-Dependent Defect Spectroscopy”. In: Proceedings of the International Reliability Physics Symposium (IRPS). 2013, pp. 2D.2.1–2D.2.7.
-
[135] J.M.M. de Nijs, K.G. Druijf, V.V. Afanas’ev, E. van der Drift, and P. Balk. “Hydrogen Induced Donor-Type Si/SiO2 Interface States”. In: Applied Physics Letters 65.19 (1994), pp. 2428–2430.
-
[136] E. Cartier and J.H. Stathis. “Atomic Hydrogen-Induced Degradation of the Si/SiO2 Structure”. In: Microelectronic Engineering 28.1-4 (1995), pp. 3–10.
-
[137] E. Cartier. “Characterization of the Hot-Electron-Induced Degradation in Thin SiO2 Gate Oxides”. In: Microelectronics Reliability 38.2 (1998), pp. 201–211.
-
[138] V.V. Afanas’ev and A. Stesmans. “Hydrogen-Induced Valence Alternation State at SiO2 Interfaces”. In: Physical Review Letters 80 (23 1998), pp. 5176–5179.
-
[139] M. Nelhiebel, J. Wissenwasser, T. Detzel, A. Timmerer, and E. Bertagnolli. “Hydrogen-Related Influence of the Metallization Stack on Characteristics and Reliability of a Trench Gate Oxide”. In: Microelectronics Reliability 45 (2005), pp. 1355–1359.
-
[140] Z. Liu, S. Fujieda, H. Ishigaki, M. Wilde, and K. Fukutani. “Current Understanding of the Transport Behavior of Hydrogen Species in MOS Stacks and Their Relation to Reliability Degradation”. In: ECS Transactions 35.4 (2011), pp. 55–72.
-
[141] G. Kapila, N. Goyal, V.D. Maheta, C. Olsen, K. Ahmed, and S. Mahapatra. “A Comprehensive Study of Flicker Noise in Plasma Nitrided SiON p-MOSFETs: Process Dependence of Pre-Existing and NBTI Stress Generated Trap Distribution Profiles”. In: Proceedings of the International Electron Devices Meeting (IEDM). 2008, pp. 103–106.
-
[142] J.P. Campbell, P.M. Lenahan, A.T. Krishnan, and S. Krishnan. “Observations of NBTI-Induced Atomic-Scale Defects”. In: IEEE Transactions on Device and Materials Reliability 6.2 (2006), pp. 117–122.
-
[143] D.L. Griscom. “Diffusion of Radiolytic Molecular Hydrogen as a Mechanism for the Post-Irradiation Buildup of Interface States in SiO2 -on-Si Structures”. In: Journal of Applied Physics 58.7 (1985), pp. 2524–2533.
-
[144] L. Tsetseris, X.J. Zhou, D.M. Fleetwood, R.D. Schrimpf, and S.T. Pantelides. “Hydrogen-Related Instabilities in MOS Devices Under Bias Temperature Stress”. In: IEEE Transactions on Device and Materials Reliability 7.4 (2007), pp. 502–508.
-
[145] A. Stesmans. “Dissociation Kinetics of Hydrogen-Passivated
Defects at the (111)Si/SiO2 Interface”. In: Physical Review B 61.12 (2000), pp. 8393–8403.
-
[146] A.C.T. van Duin, A. Strachan, S. Stewman, Q. Zhang, X. Xu, and W. Goddard. “Reaxff for Si SiO systems”. In: Journal of Physical Chemistry A 107 (2003), pp. 3803–3811.
-
[147] S. Plimpton. “Fast Parallel Algorithms for Short-Range Molecular Dynamics”. In: Journal of Computational Physics 117 (1995), pp. 1–19.
-
[148] W.M. Haynes. CRC handbook of chemistry and physics. CRC press, 2014.
-
[149] B. El-Kareh. “Fundamentals of Semiconductor Processing Technologies 1995”. In: Norwell, Massachusetts: Kluwer Academic Publisher ().
-
[150] J. VandeVondele, M. Krack, F. Mohamed, M. Parrinelo, T. Chassaing, and J. Hutter. “Quickstep: Fast and accurate DFT”. In: Computer Physics Communications 167 (2005), p. 103.
-
[151] J. VandeVondele and J. Hutter. “Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases”. In: The Journal of Chemical Physics 127.11 (2007), p. 114105.
-
[152] S. Goedecker, M. Teter, and J. Hutter. “Separable dual-space gaussian pseudopotentials”. In: Physical Review B 54 (1996), pp. 1703–1710.
-
[153] C.G. Broyden. “The convergence of a class of double-rank minimization algorithms 1. general considerations”. In: IMA Journal of Applied Mathematics 6.1 (1970), pp. 76–90.
-
[154] R. Fletcher. “A new approach to variable metric algorithms”. In: The computer journal 13.3 (1970), pp. 317–322.
-
[155] D. Goldfarb. “A family of variable-metric methods derived by variational means”. In: Mathematics of computation 24.109 (1970), pp. 23–26.
-
[156] D.F. Shanno. “Conditioning of quasi-Newton methods for function minimization”. In: Mathematics of computation 24.111 (1970), pp. 647–656.
-
[157] A.-M. El-Sayed, M.B. Watkins, V.V. Afanas’ev, and A.L. Shluger. “Nature of intrinsic and extrinsic electron trapping in SiO2 ”. In: Physical Review B 89.12 (2014), p. 125201. issn: 1098-0121.
-
[158] P.E. Blöchl and J.H. Stathis. “Hydrogen Electrochemistry and Stress-Induced Leakage Current in Silica”. In: Physical Review Letters 83 (2 1999), pp. 372–375.
-
[159] P.E. Blöchl. “First-Principles Calculations of Defects in Oxygen-Deficient Silica Exposed to Hydrogen”. In: Physical Review B 62.10 (2000), pp. 6158–6179.
-
[160] F. Schanovsky, W. Gös, and T. Grasser. “Multiphonon Hole Trapping from First Principles”. In: Journal of Vacuum Science & Technology B 29.1 (2011), 01A2011–01A2015.
-
[161] P.V. Sushko, S. Mukhopadhyay, A.S. Mysovsky, V.B. Sulimov, A. Taga, and A.L. Shluger. “Structure and properties of defects in amorphous silica: new insights from embedded cluster calculations”. In: Journal of Physics: Condensed Matter 17.21 (2005), S2115.
-
[162] A.V. Kimmel, P.V. Sushko, A.L. Shluger, and G. Bersuker. “Positive and Negative Oxygen Vacancies in Amorphous Silica”. In: Silicon Nitride, Silicon Dioxide, and Emerging Dielectrics 10. Ed. by R. Sah, J. Zhang, Y. Kamakura, M. Deen, and J. Yota. Vol. 19. ECS Transactions, 2009, pp. 2–17.
-
[163] N.L. Anderson, R. Pramod Vedula, P.A. Schultz, R.M. van Ginhoven, and A. Strachan. “Defect level distributions and atomic relaxations induced by charge trapping in amorphous silica”. In: Applied Physics Letters 100.17 (2012), p. 172908.
-
[164] S.P. Karna, H.A. Kurtz, A.C. Pineda, W.M. Shedd, and R.D. Pugh. “Point defects in Si-SiO2 systems: current understanding”. In: Defects in SiO2 and Related Dielectrics: Science and Technology. Springer, 2000, pp. 599–615.
-
[165] E.H. Poindexter and W.L. Warren. “Paramagnetic Point Defects in Amorphous Thin Films of SiO2 and Si3 N4 : Updates and Additions”. In: Journal of the Electrochemical Society 142.7 (1995), pp. 2508–2516.
-
[166] K.L. Yip and W.B. Fowler. “Electronic structure of E 10 centers in SiO2 ”. In: Physical Review B 11.6 (1975), p. 2327.
-
[167] E.P. O’Reilly and J. Robertson. “Theory of defects in vitreous silicon dioxide”. In: Physical Review B 27.6 (1983), p. 3780.
-
[168] V.B. Sulimov, P.V. Sushko, A.H. Edwards, A.L. Shluger, and A.M. Stoneham. “Asymmetry and long-range character of lattice deformation by neutral oxygen vacancy in α-quartz”. In: Physical Review B 66.2 (2002), p. 024108.
-
[169] M. Busso, S. Casassa, C. Pisani, and V.B. Sulimov. “Ab initio simulation of the oxygen vacancy bistability in pure and Ge-doped α-quartz”. In: Model. and Simul. in Mat. Science and Engineering 10.1 (2002), p. 21.
-
[170] D.J. Chadi. “Negative-U property of the oxygen vacancy defect in SiO2 and its implication for the E0 1 center in α-quartz”. In: Applied Physics Letters 83.3 (2003), pp. 437–439.
-
[171] L. Martin-Samos, Y. Limoge, N. Richard, J.P. Crocombette, G. Roma, E. Anglada, and E. Artacho. “Oxygen neutral defects in silica: Origin of the distribution of the formation energies”. In: Europhysics Letters 66.5 (2004), p. 680.
-
[172] J.K. Rudra, W.B. Fowler, and F.J. Feigl. “Model for the E 20 Center in Alpha Quartz”. In: Physical Review Letters 55.23 (1985), p. 2614.
-
[173] Z.-Y. Lu, C.J. Nicklaw, D.M. Fleetwood, R.D. Schrimpf, and S.T. Pantelides. “Structure, Properties, and Dynamics of Oxygen Vacancies in Amorphous SiO2 ”. In: Physical Review Letters 89.28 (2002), p. 285505.
-
[174] S. Mukhopadhyay, P.V. Sushko, A.M. Stoneham, and A.L. Shluger. “Modeling of the structure and properties of oxygen vacancies in amorphous silica”. In: Physical Review B 70.19 (2004), p. 195203.
-
[175] C.J. Nicklaw, Z.-Y. Lu, D.M. Fleetwood, R.D. Schrimpf, and S.T. Pantelides. “The structure, properties, and dynamics of oxygen vacancies in amorphous SiO2 ”. In: IEEE Transactions on Nuclear Science 49.6 (2002), pp. 2667–2673.
-
[176] S. Mukhopadhyay, P.V. Sushko, A.M. Stoneham, and A.L. Shluger. “Correlation between the atomic structure, formation energies, and optical absorption of neutral oxygen vacancies in amorphous silica”. In: Physical Review B 71.23 (2005), p. 235204.
-
[177] P.V. Sushko, S. Mukhopadhyay, A.M. Stoneham, and A.L. Shluger. “Oxygen vacancies in amorphous silica: structure and distribution of properties”. In: Microelectronic Engineering 80 (2005), pp. 292–295.
-
[178] M. Boero, A. Pasquarello, J. Sarnthein, and R. Car. “Structure and hyperfine parameters of E 10 centers in α-quartz and in vitreous SiO2 ”. In: Physical Review Letters 78.5 (1997), p. 887.
-
[179] A.-M. El-Sayed, M.B. Watkins, T. Grasser, V.V. Afanas’ev, and A.L. Shluger. “Hydrogen induced rupture of strained Si-O bonds in amorphous silicon dioxide”. In: Physical Review Letters 114.11 (2015), p. 115503.
-
[180] Vienna Scientific Cluster. http://vsc.ac.at/systems/. Accessed: 2017-06-01.
-
[181] T. Grasser, P.-J. Wagner, H. Reisinger, T. Aichinger, G. Pobegen, M. Nelhiebel, and B. Kaczer. “Analytic Modeling of the Bias Temperature Instability Using Capture/Emission Time Maps”. In: Proceedings of the International Electron Devices Meeting (IEDM). 2011, pp. 27.4.1–27.4.4.
-
[182] R.S. Mulliken. “Electronic population analysis on LCAO–MO molecular wave functions. I”. In: The Journal of Chemical Physics 23.10 (1955), pp. 1833–1840.
-
[183] R.A. Marcus. “Exchange reactions and electron transfer reactions including isotopic exchange. Theory of oxidation-reduction reactions involving electron transfer. Part 4.-A statistical-mechanical basis for treating contributions from solvent, ligands, and inert salt”. In: Discussions of th Faraday Society 29 (1960), pp. 21–31.
-
[184] S.J. Pearton, J.W. Corbett, and M. Stavola. Hydrogen in crystalline semiconductors. Vol. 16. Springer Science & Business Media, 2013.
-
[185] C.G. Van de Walle and B.R. Tuttle. “Microscopic theory of hydrogen in silicon devices”. In: IEEE Transactions on Electron Devices 47.10 (2000), pp. 1779–1786.
-
[186] W. Weibull et al. “A statistical distribution function of wide applicability”. In: Journal of applied mechanics 18.3 (1951), pp. 293–297.
-
[187] F.W. Zok. “On weakest link theory and Weibull statistics”. In: Journal of the American Ceramic Society 100.4 (2017), pp. 1265–1268.
-
[188] A. Wormsen and G. Härkegård. “A statistical investigation of fatigue behaviour according to Weibull’s weakest link theory”. In: ECF15, Stockolm 2004.
-
[189] J.M. Soon, K.P. Loh, S.S. Tan, T.P. Chen, W.Y. Teo, and L. Chan. “Study of Negative-Bias Temperature-Instability-Induced Defects using First-Principle Approach”. In: Applied Physics Letters 83.15 (2003), pp. 3063–3065.
-
[190] J. Godet, F. Giustino, and A. Pasquarello. “Proton-Induced Fixed Positive Charge at the SiO2 Interface”. In: Physical Review Letters 99.12 (2007), pp. 126102-1–126102-4.
-
[191] M. Wilde, M. Matsumoto, and K. Fukutani. “Influence of H2-annealing on the hydrogen distribution near SiO2 /Si(100) interfaces revealed by in situ nuclear reaction analysis”. In: Journal of Applied Physics 92 (2002), pp. 4320–4329.
-
[192] Y. Wang, B. Fowler, Y.-T. Chen, F. Xue, F. Zhou, Y.-F. Chang, and J.C. Lee. “Effect of hydrogen/deuterium incorporation on electroforming voltage of SiOx resistive random access memory”. In: Applied Physics Letters 101.18 (2012), p. 183505.
-
[193] D.S. Ang, Z.Q. Teo, T.J.J. Ho, and C.M. Ng. “Reassessing the Mechanisms of Negative-Bias Temperature Instability by Repetitive Stress/Relaxation Experiments”. In: IEEE Transactions on Device and Materials Reliability 11.1 (2011), pp. 19–34.
-
[194] N.H. Nickel, A. Yin, and S.J. Fonash. “Influence of Hydrogen and Oxygen Plasma Treatments on Grain-Boundary Defects in Polycrystalline Silicon”. In: Applied Physics Letters 65.24 (1994), pp. 3099–3101.
-
[195] E.H. Poindexter. “Chemical Reactions of Hydrogeneous Species in the Si/SiO2 System”. In: Journal of Non-Crystalline Solids 187 (1995), pp. 257–263.
-
[196] M. Waltl, P.-J. Wagner, H. Reisinger, K. Rott, and T. Grasser. “Advanced Data Analysis Algorithms for the Time-Dependent Defect Spectroscopy of NBTI”. In: Proceedings of the International Integrated Reliability Workshop (IIRW). 2012, pp. 74–79.
-
[197] M. Waltl, A. Grill, G. Rzepa, W. Gös, J. Franco, B. Kaczer, J. Mitard, and T. Grasser. “Nanoscale Evidence for the Superior Reliability of SiGe High-k pMOSFETs”. In: Proceedings of the International Reliability Physics Symposium (IRPS). 2016, XT-02-1-XT-02-6.
-
[198] S.T. Pantelides, L. Tsetseris, S.N. Rashkeev, X.J. Zhou, D.M. Fleetwood, and R.D. Schrimpf. “Hydrogen in MOSFETs–A primary agent of reliability issues”. In: Microelectronics Reliability 47.6 (2007), pp. 903–911.
-
[199] S.A. Sheikholeslam, H. Manzano, C. Grecu, and A. Ivanov. “Reduced hydrogen diffusion in strained amorphous SiO2 : understanding ageing in MOSFET devices”. In: Journal of Materials Chemistry C 4.34 (2016), pp. 8104–8110.
-
[200] J. Godet and A. Pasquarello. “Proton Diffusion Mechanism in Amorphous SiO2 ”. In: Physical Review Letters 97 (15 2006), p. 155901.
-
[201] H.A. Kurtz and S.P. Karna. “Proton mobility in a-SiO2 ”. In: IEEE Transactions on Nuclear Science 46.6 (1999), pp. 1574–1577.
-
[202] Q. Zhang, S. Tang, and R.M. Wallace. “Proton trapping and diffusion in SiO2 thin films: a first-principles study”. In: Applied Surface Science 172.1 (2001), pp. 41–46.
-
[203] T.E. Tsai, D.L. Griscom, and E.J. Friebele. “Medium-range structural order and fractal annealing kinetics of radiolytic atomic hydrogen in high-purity silica”. In: Physical Review B 40.9 (1989), p. 6374.
-
[204] I.A. Shkrob and A.D. Trifunac. “Time-resolved EPR of spin-polarized mobile H atoms in amorphous silica: The involvement of small polarons”. In: Physical Review B 54.21 (1996), p. 15073.
-
[205] B. Tuttle. “Energetics and diffusion of hydrogen in SiO2 ”. In: Physical Review B 61 (7 2000), pp. 4417–4420.
-
[206] A. Yokozawa and Y. Miyamoto. “First-principles calculations for charged states of hydrogen atoms in SiO2 ”. In: Physical Review B 55.20 (1997), p. 13783.
-
[207] F.B. McLean. “A Framework for Understanding Radiation-Induced Interface States in SiO2 Structures”. In: IEEE Transactions on Nuclear Science 27.6 (1980), pp. 1651–1657.
-
[208] K. Vanheusden, W.L. Warren, and R.A.B. Devine. “H+ and D+ associated charge buildup during annealing of Si/SiO2 /Si structures”. In: Journal of non-crystalline solids 216 (1997), pp. 116–123.
-
[209] R.E. Stahlbush, R.K. Lawrence, and H.L. Hughes. “
Motion in SiO2 : Incompatible Results from Hydrogen-Annealing and Radiation Models”. In: IEEE Transactions on Nuclear Science 45.6 (1998), pp. 2398–2407.
-
[210] R.A.B. Devine and G.V. Herrera. “Electric-field-induced transport of protons in amorphous SiO2 ”. In: Physical Review B 63 (23 2001), p. 233406.
-
[211] P.E. Bunson, M. Di Ventra, S.T. Pantelides, R.D. Schrimpf, and K.F. Galloway. “Ab initio calculations of H/sup+/energetics in SiO/sub 2: Implications for transport”. In: IEEE Transactions on Nuclear Science 46.6 (1999), pp. 1568–1573.
-
[212] H.M. Aktulga, J.C. Fogarty, S.A. Pandit, and A.Y. Grama. “Parallel reactive molecular dynamics: Numerical methods and algorithmic techniques”. In: Parallel Computing 38.4 (2012), pp. 245–259.
-
[213] S. Smidstrup, A. Pedersen, K. Stokbro, and H. Jónsson. “Improved initial guess for minimum energy path calculations”. In: The Journal of Chemical Physics 140.21 (2014), p. 214106.
-
[214] S. Le Roux and P. Jund. “Ring statistics analysis of topological networks: New approach and application to amorphous GeS 2 and SiO2 systems”. In: Computational Materials Science 49.1 (2010), pp. 70–83.
-
[215] S.V. King. “Ring configurations in a random network model of vitreous silica”. In: Nature 213 (1967), pp. 1112–1113.
-
[216] D.S. Franzblau. “Computation of ring statistics for network models of solids”. In: Physical Review B 44 (10 1991), pp. 4925–4930.
-
[217] P.J. McMillan. “Mass models of the Milky Way”. In: Monthly Notices of the Royal Astronomical Society 414.3 (2011), pp. 2446–2457.
-
[218] K. Croswell. “The alchemy of the heavens.” In: Oxford University Press (1996).
-
[219] A. Nitzan. “Electron Transfer Processes”. In: Chemical dynamics in condensed phases: relaxation, transfer and reactions in condensed molecular systems. Oxford University Press, 2006, pp. 483–535.
-
[220] A.M. Stoneham. “Non-radiative Transitions in Semiconductors”. In: Reports on Progress in Physics 44 (1981), pp. 1251–1295.
-
[221] V. May and O. Kühn. Charge and energy transfer dynamics in molecular systems. John Wiley & Sons, 2008.
-
[222] Z. Cheng. “Unified Quantum Field Theory of Light Absorption by Defect Centers”. In: Physical Review B 23.60 (1999), pp. 15747–15765.
-
[223] J. Ulstrup. Charge transfer processes in condensed media. Vol. 10. Springer Science & Business Media, 2012.
-
[224] S.G. Christov. “A general oscillator model for charge transfer in polar media”. In: Journal of the Electrochemical Society 124.1 (1977), pp. 69–78.
-
[225] J.W. Gadzuk and S. Holloway. “Charge transfer and vibrational excitation in molecule-surface collisions: Trajectorized quantum theory”. In: Physica Scripta 32.4 (1985), p. 413.
-
[226] T. Markvart. “Multiphonon Transitions between Adiabatic Potential Curves”. In: Journal of Physics C: Solid State Physics 17 (1984), pp. 6303–6316.
-
[227] T. Knobloch. “Characterization and Physical Modeling of Degradation in MoS2 Transistors”. MA thesis. TU Wien, E360, 2016.
-
[228] N.T. Bagraev and V.A. Mashkov. “A mechanism for two-electron capture at deep level defects in semiconductors”. In: Solid State Communications 65.10 (1988), pp. 1111–1117.
-
[229] C.G. Van de Walle and J. Neugebauer. “First-principles calculations for defects and impurities: Applications to III-nitrides”. In: Journal of Applied Physics 95.8 (2004), pp. 3851–3879.
-
[230] S.B. Zhang and J.E. Northrup. “Chemical potential dependence of defect formation energies in GaAs: Application to Ga self-diffusion”. In: Physical Review Letters 67 (17 1991), pp. 2339–2342.
-
[231] A. Alkauskas, P. Broqvist, and A. Pasquarello. “Defect energy levels in density functional calculations: Alignment and band gap problem”. In: Physical Review Letters 101.4 (2008), p. 046405.
-
[232] S. Lany and A. Zunger. “Assessment of correction methods for the band-gap problem and for finite-size effects in supercell defect calculations: Case studies for ZnO and GaAs”. In: Physical Review B 78.23 (2008), p. 235104.
-
[233] Y. Kumagai and F. Oba. “Electrostatics-based finite-size corrections for first-principles point defect calculations”. In: Physical Review B 89.19 (2014), p. 195205.
-
[234] H.-P. Komsa, T.T. Rantala, and A. Pasquarello. “Finite-size supercell correction schemes for charged defect calculations”. In: Physical Review B 86 (4 2012), p. 045112.
-
[235] C. Freysoldt, J. Neugebauer, and C.G. Van de Walle. “Fully ab initio finite-size corrections for charged-defect supercell calculations”. In: Physical Review Letters 102.1 (2009), p. 016402.
-
[236] E. Madelung. “Das elektrische Feld in Systemen von regelmäßig angeordneten Punktladungen”. In: Zeitschrift für Physik 19 (1918), pp. 524–532.
-
[237] G. Makov and M.C. Payne. “Periodic boundary conditions in ab initio calculations”. In: Physical Review B 51.7 (1995), p. 4014.
-
[238] J.P. Perdew. “Density functional theory and the band gap problem”. In: International Journal of Quantum Chemistry 28.S19 (1985), pp. 497–523.
-
[239] S.B. Zhang. “The microscopic origin of the doping limits in semiconductors and wide-gap materials and recent developments in overcoming these limits: a review”. In: Journal of Physics: Condensed Matter 14.34 (2002), R881.
-
[240] S. Lany and A. Zunger. “Polaronic hole localization and multiple hole binding of acceptors in oxide wide-gap semiconductors”. In: Physical Review B 80 (8 2009), p. 085202.
-
[241] N.E. Christensen. “Electronic structure of GaAs under strain”. In: Physical Review B 30.10 (1984), p. 5753.
-
[242] W. Gös, M. Toledano-Luque, F. Schanovsky, M. Bina, O. Baumgartner, B. Kaczer, and T. Grasser. “Multi-Phonon Processes as the Origin of Reliability Issues”. In: ECS Transactions. 2013, pp. 31–47.
-
[243] M. Fréchet. “Sur la loi de probabilité de l’écart maximum”. In: Annales de la societe Polonaise de Mathematique. [sn]. 1928.
-
[244] P. Rosin and E. Rammler. “The laws governing the fineness of powdered coal”. In: Journal of the Institute of Fuel 7 (1933), pp. 29–36.
-
[245] H. Rinne. The Weibull distribution: a handbook. CRC Press, 2008.
-
[246] J.I. McCool. Using the Weibull distribution: reliability, modeling and inference. Vol. 950. John Wiley & Sons, 2012.
-
[247] I.N. Bronstein, J. Hromkovic, B. Luderer, H.-R. Schwarz, J. Blath, A. Schied, S. Dempe, G. Wanka, S. Gottwald, E. Zeidler, et al. Taschenbuch der Mathematik. Vol. 6. Verlag Harri Deutsch, 2005.
-
[248] S.Y.D. Dubey. “Normal and Weibull distributions”. In: Naval Research Logistics (NRL) 14.1 (1967), pp. 69–79.
List of Publications
Publications in Scientific Journals
-
[YWJ1] Wimmer, Yannick, Al-Moatasem El-Sayed, Wolfgang Gös, Tibor Grasser, and Alexander L. Shluger. “Role of Hydrogen in Volatile Behaviour of Defects in SiO2 -Based Electronic Devices”. In: Proceedings of the Royal Society A 472.2190 (2016). invited, pp. 1–23.
-
[YWJ2] Al-Moatasem El-Sayed, Wimmer, Yannick, Wolfgang Gös, Tibor Grasser, Valeri V. Afanas’ev, and Alexander L. Shluger. “Theoretical Models of Hydrogen-Induced Defects in Amorphous Silicon Dioxide”. In: Physical Review B 92.11 (2015), p. 014107.
-
[YWJ3] Wolfgang Gös, Wimmer, Yannick, Al-Moatasem El-Sayed, Gerhard Rzepa, Alexander L. Shluger, and Tibor Grasser. “Modeling of Oxide Defects in Semiconductor Devices: Connecting First-Principles with Rate Equations”. In: Microelectronics Reliability (submitted).
-
[YWJ4] Markus Bina, Stanislav E. Tyaginov, Jacopo Franco, Karl Rupp, Wimmer, Yannick, Dimitry Osintsev, Ben Kaczer, and Tibor Grasser. “Predictive Hot-Carrier Modeling of n-Channel MOSFETs”. In: IEEE Transactions on Electron Devices 61.9 (2014), pp. 3103–3110.
-
[YWJ5] Stanislav E. Tyaginov, Wimmer, Yannick, and Tibor Grasser. “Modeling of Hot-Carrier Degradation Based on Thorough Carrier Transport Treatment”. In: Facta Universitatis 27.4 (2014). invited, pp. 479–508.
-
[YWJ6] Stanislav E. Tyaginov, Markus Bina, Jacopo Franco, Wimmer, Yannick, Ben Kaczer, and Tibor Grasser. “On the Importance of Electron-Electron Scattering for Hot-Carrier Degradation”. In: Japanese Journal of Applied Physics 54 (2015), pp. 1–6.
-
[YWJ7] Prateek Sharma, Stanislav E. Tyaginov, Wimmer, Yannick, Florian Rudolf, Karl Rupp, Hubert Enichlmair, Jong M. Park, Hajdin Ceric, and Tibor Grasser. “Comparison of Analytic Distribution Function Models for Hot-Carrier Degradation in nLDMOSFETs”. In: Microelectronics Reliability 55.9-10 (2015), pp. 1427–1432.
-
[YWJ8] Prateek Sharma, Stanislav E. Tyaginov, Wimmer, Yannick, Florian Rudolf, Karl Rupp, Markus Bina, Hubert Enichlmair, Jong M. Park, Rainer Minixhofer, Hajdin Ceric, and Tibor Grasser. “Modeling of Hot-Carrier Degradation in nLDMOS Devices: Different Approaches to the Solution of the Boltzmann Transport Equation”. In: IEEE Transactions on Electron Devices 62.6 (2015), pp. 1811–1818.
-
[YWJ9] Prateek Sharma, Stanislav E. Tyaginov, Markus Jech, Wimmer, Yannick, Florian Rudolf, Hubert Enichlmair, Jong M. Park, Hajdin Ceric, and Tibor Grasser. “The Role of Cold Carriers and the Multiple-Carrier Process of Si-H Bond Dissociation for Hot-Carrier Degradation in n- and p-channel LDMOS Devices”. In: Solid-State Electronics 115.Part B (2016), pp. 185–191.
Contributions in Conference Proceedings
-
[YWC1] Tibor Grasser, Michael Waltl, Wimmer, Yannick, Wolfgang Gös, Robert Kosik, Gerhard Rzepa, Hans Reisinger, Gregor Pobegen, Al-Moatasem El-Sayed, Alexander L. Shluger, and Ben Kaczer. “Gate-Sided Hydrogen Release as the Origin of “Permanent” NBTI Degradation: From Single Defects to Lifetimes”. In: Proceedings of the International Electron Devices Meeting (IEDM). Dec. 2015.
-
[YWC2] Tibor Grasser, Wolfgang Gös, Wimmer, Yannick, Franz Schanovsky, Gerhard Rzepa, Michael Waltl, Karina Rott, Hans Reisinger, Valeri V. Afanas’ev, Andre Stesmans, Al-Moatasem El-Sayed, and Alexander L. Shluger. “On the Microscopic Structure of Hole Traps in pMOSFETs”. In: Proceedings of the International Electron Devices Meeting (IEDM). Dec. 2014.
-
[YWC3] Tibor Grasser, Michael Waltl, Gerhard Rzepa, Wolfgang Gös, Wimmer, Yannick, Al-Moatasem El-Sayed, Alexander L. Shluger, Hans Reisinger, and Ben Kaczer. “The ”Permanent” Component of NBTI Revisited: Saturation, Degradation-Reversal, and Annealing”. In: talk: International Reliability Physics Symposium (IRPS), Pasadena, CA, USA; 2016-04-17 – 2016-04-21. 2016, 5A-2-1–5A-2-8.
-
[YWC4] Tibor Grasser, Michael Waltl, Wolfgang Gös, Wimmer, Yannick, Al-Moatasem El-Sayed, Alexander L. Shluger, and Ben Kaczer. “On the Volatility of Oxide Defects: Activation, Deactivation, and Transformation”. In: talk: International Reliability Physics Symposium (IRPS), Monterey, CA, USA; 2015-04-19 – 2015-04-23. IEEE, 2015, 5A.3.1–5A.3.8.
-
[YWC5] Wimmer, Yannick, Wolfgang Gös, Al-Moatasem El-Sayed, Alexander L. Shluger, and Tibor Grasser. “A Density-Functional Study of Defect Volatility in Amorphous Silicon Dioxide”. In: Proceedings of the International Conference on Simulation of Semiconductor Processes and Devices (SISPAD). talk: International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Washington DC, USA; 2015-09-09 – 2015-09-11. 2015, pp. 44–47.
-
[YWC6] Wimmer, Yannick, Wolfgang Gös, Al-Moatasem El-Sayed, Alexander L. Shluger, and Tibor Grasser. “On the Validity of the Harmonic Potential Energy Surface Approximation for Nonradiative Multiphonon Charge Transitions in Oxide Defects”. In: Proceedings of the International Workshop on Computational Electronics (IWCE). talk: International Workshop on Computational Electronics (IWCE), West Lafayette, Indiana, USA; 2015-09-02 – 2015-09-04. 2015, pp. 97–98.
-
[YWC7] Stanislav E. Tyaginov, Markus Bina, Jacopo Franco, Dimitry Osintsev, Wimmer, Yannick, Ben Kaczer, and Tibor Grasser. “Essential Ingredients for Modeling of Hot-Carrier Degradation in Ultra-Scaled MOSFETs”. In: Proceedings of the International Integrated Reliability Workshop (IIRW). talk: IEEE International Reliability Workshop (IIRW), South Lake Tahoe, USA; 2013-10-13 – 2013-10-17. 2013, pp. 98–101.
-
[YWC8] Florian Rudolf, Wimmer, Yannick, Josef Weinbub, Karl Rupp, and Siegfried Selberherr. “Mesh Generation Using Dynamic Sizing Functions”. In: Proceedings of the 4th European Seminar on Computing. talk: European Seminar on Computing (ESCO), Pilsen, Czech Republic; 2014-06-15 – 2014-06-20. 2014, p. 191.
-
[YWC9] Stanislav E. Tyaginov, Markus Bina, Jacopo Franco, Wimmer, Yannick, Dimitry Osintsev, Ben Kaczer, and Tibor Grasser. “A Predictive Physical Model for Hot-Carrier Degradation in Ultra-Scaled MOSFETs”. In: Proceedings of the International Conference on Simulation of Semiconductor Processes and Devices (SISPAD). talk: International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Yokohama, Japan; 2014-09-09 – 2014-09-11. 2014, pp. 89–92.
-
[YWC10] Karl Rupp, Markus Bina, Wimmer, Yannick, Ansgar Jungel, and Tibor Grasser. “Cell-Centered Finite Volume Schemes for Semiconductor Device Simulation”. In: Proceedings of the International Conference on Simulation of Semiconductor Processes and Devices (SISPAD). talk: International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Yokohama, Japan; 2014-09-09 – 2014-09-11. 2014, pp. 365–368.
-
[YWC11] Wolfgang Gös, Michael Waltl, Wimmer, Yannick, Gerhard Rzepa, and Tibor Grasser. “Advanced Modeling of Charge Trapping: RTN, 1/f noise, SILC, and BTI”. In: Proceedings of the International Conference on Simulation of Semiconductor Processes and Devices (SISPAD). invited; talk: International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Yokohama, Japan; 2014-09-09 – 2014-09-11. 2014, pp. 77–80.
-
[YWC12] Wimmer, Yannick, Stanislav E. Tyaginov, Florian Rudolf, Karl Rupp, Markus Bina, Hubert Enichlmair, Jong M. Park, Rainer Minixhofer, Hajdin Ceric, and Tibor Grasser. “Physical Modeling of Hot-Carrier Degradation in nLDMOS Transistors”. In: Proceedings of the International Integrated Reliability Workshop (IIRW). talk: IEEE International Reliability Workshop (IIRW), South Lake Tahoe, CA, USA; 2014-10-12 – 2014-10-16. IEEE, 2014, pp. 58–62.
-
[YWC13] Stanislav E. Tyaginov, Markus Bina, Jacopo Franco, Wimmer, Yannick, Florian Rudolf, Hubert Enichlmair, Jong M. Park, Ben Kaczer, Hajdin Ceric, and Tibor Grasser. “Dominant Mechanism of Hot-Carrier Degradation in Short- and Long-Channel Transistors”. In: Proceedings of the International Integrated Reliability Workshop (IIRW). talk: IEEE International Reliability Workshop (IIRW), South Lake Tahoe, CA, USA; 2014-10-12 – 2014-10-16. 2014, pp. 63–68.
-
[YWC14] Prateek Sharma, Stanislav E. Tyaginov, Wimmer, Yannick, Florian Rudolf, Hubert Enichlmair, Jong M. Park, Hajdin Ceric, and Tibor Grasser. “A Model for Hot-Carrier Degradation in nLDMOS Transistors Based on the Exact Solution of the Boltzmann Transport Equation Versus the Drift-Diffusion Scheme”. In: Proceedings of 2015 Joint International EUROSOI Workshop and International Conference on Ultimate Integration on Silicon. talk: Joint International EUROSOI Workshop and International Conference on Ultimate Integration on Silicon (EUROSOI-ULIS), Bologna, Italy; 2015-01-26 – 2015-01-28. IEEE, 2015, pp. 21–24.
-
[YWC15] Ben Kaczer, Jacopo Franco, Minki Cho, Tibor Grasser, Philippe J. Roussel, Stanislav E. Tyaginov, Markus Bina, Wimmer, Yannick, Luis M. Procel, Leonel Trojman, Felice Crupi, Gregory Pitner, Vamsi Putcha, Pieter Weckx, Erik Bury, Zhengping Ji, An De Keersgieter, Thomas Chiarella, Naoto Horiguchi, Guido Groeseneken, and Aaron Thean. “Origins and Implications of Increased Channel Hot Carrier Variability in nFinFETs”. In: Proceedings of the International Reliability Physics Symposium (IRPS). talk: International Reliability Physics Symposium (IRPS), Monterey, CA, USA; 2015-04-19 – 2015-04-23. 2015.
-
[YWC16] Prateek Sharma, Stanislav E. Tyaginov, Wimmer, Yannick, Florian Rudolf, Karl Rupp, Markus Bina, Hubert Enichlmair, Jong M. Park, Hajdin Ceric, and Tibor Grasser. “Predictive and Efficient Modeling of Hot-Carrier Degradation in nLDMOS Devices”. In: talk: International Symposium on Power Semiconductor Devices and ICs (ISPSD), Hong Kong, China; 2015-05-10 – 2015-05-14. 2015, pp. 389–392.
-
[YWC17] Prateek Sharma, Stanislav E. Tyaginov, Wimmer, Yannick, Florian Rudolf, Karl Rupp, Hubert Enichlmair, Jong M. Park, Hajdin Ceric, and Tibor Grasser. “Comparison of Analytic Distribution Function Models for Hot-Carrier Degradation in nLDMOSFETs”. In: Proceedings of the European Symposium on Reliability of Electron Devices, Failure Physics and Analysis (ESREF). talk: European Symposium on Reliability of Electron Devices, Failure Physics and Analysis (ESREF), Toulouse, France; 2015-10-05 – 2015-10-09. 2015, p. 60.