|
|
Si |
GaAs |
3C-SiC |
6H-SiC |
4H-SiC |
Diamond |
Lattice 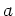 [Å] [Å] |
5.43 |
5.65 |
4.36 |
3.08 |
3.08 |
3.567 |
Lattice 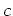 [Å] [Å] |
n.a. |
n.a. |
n.a. |
10.05 |
15.12 |
n.a. |
|
Bond length [Å] |
2.35 |
2.45 |
1.89 |
1.89 |
1.89 |
1.54 |
TEC [10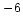 /K] /K] |
2.6 |
5.73 |
3.0 |
4.5 |
- |
0.8 |
Density [gm/cm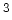 ] ] |
2.3 |
5.3 |
3.2 |
3.2 |
3.2 |
3.5 |
|
Ther. cond. [W/cmK] |
1.5 |
0.5 |
5 |
5 |
5 |
20 |
Melting point [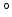 C] C] |
1420 |
1240 |
2830 |
2830 |
2830 |
4000 |
|
Mohs hardness |
|
|
9 |
9 |
9 |
10 |
TEC = thermal expansion coefficient
|