 -
-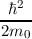 ∇r2 -
∇r2 -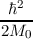 ∇R2 + H
ion-ion(R)
∇R2 + H
ion-ion(R) Ψ(r,R) = iℏ∂tΨ(r,R),
Ψ(r,R) = iℏ∂tΨ(r,R),Modelling the transport of charge carriers in a crystal, eg. silicon, containing artificially introduced impurities, ie. dopands, to modify the electrical conductance of the crystal is not an easy task. In order to fully describe the many-particle system, where r denotes the positions of the electrons and R denotes the positions of the ions, one needs to employ
 - -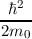 ∇r2 - ∇r2 -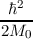 ∇R2 + H
ion-ion(R) ∇R2 + H
ion-ion(R) | |||
+ Hel-ion(r,R) + Hel-el(r) + … Ψ(r,R) = iℏ∂tΨ(r,R), Ψ(r,R) = iℏ∂tΨ(r,R), | (2.1) |
which is the time-dependent Schrödinger equation of the full many-particle system. In the above equation various interactions between the ions and electrons, such as the interactions between ions is given by the operator Hion-ion(r,R), between electrons and ions is described by Hel-ion(r,R) and electron-electron scattering is described by Hel-el(r,R). At present it is practically impossible to solve the many-particle Schrödinger equation even for only a few atoms. Thus the usual approach to this is to decouple the electron-system and the system of lattice atoms by the separation Ansatz
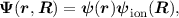 |
where the wave function ψ only describes the system of electrons and ψion only describes the lattice. Inserting this into Equation (2.1) one obtains
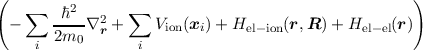 ψ(r,R) ψ(r,R) | = Eelψ(r,R), | ||
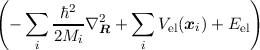 ψion(R) ψion(R) | = Eionψion(R), |
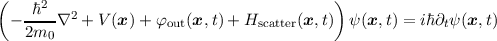 | (2.2) |
where ψ(x,t) is now a single electron wave function representing the whole ensemble of electrons, φout(x,t) is the external electrostatic potential and all other particle-particle interactions have been summarized in Hscatter. In order to obtain a semi-classical approximation in the special case of a periodic lattice Equation (2.2) has to be transformed such that the potential of the ions does not explicitly appear in the equation. This is done by solving Equation (2.2) without any scattering Hscatter and time dependence [13, 12],
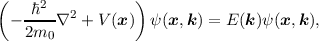 | (2.3) |
and inserting the solution back into Equation (2.2), where the reciprocal wave vector k and the ionic potential V (x) (jellium-model for semiconductors) have been introduced [12, 14]. A solution ψ(x,k) to Equation (2.3) is easily obtained by using plane-waves and Bloch-functions [15] to account for the periodicity in the lattice. Additionally the solution to Equation (2.3) gives the relation Eν(k) for the νth band. Eν(k) is often referred to as the dispersion relation and is only dependent on the type of semiconductor. By introducing the operator Eν(-i∇x), where
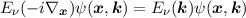 |
according to [12], one can transform Equation (2.2) into
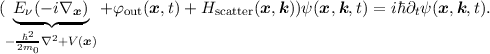 | (2.4) |
The Hamilton operators used in Equation (2.4) form the basis of all transport models that are described in the course of this thesis. Often Equation (2.4) is arbitrarily separated into two equations, one for all bands (valence bands) below and one for all conduction bands above the center of the band gap. Next a new quasi-particle, the hole, is introduced in the equation for all valence bands. A hole represents an unoccupied state and thus has a positive elementary charge associated with it. This is done, since the valence bands contain many electrons occupying the bands. Thus it is easier to describe the flow of the empty states instead. For a proper definition of holes refer to [12].