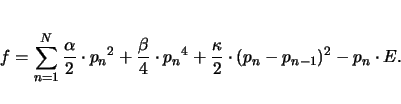 |
(3.5) |
The minimized free energy model concentrates on the double well structure of distorted perovskite structures. A one-dimensional lattice model was developed by Omura et al [OAI91], based on previous work on isomorphous ferroelectric phase transition by Ishibashi, which was published in 1992 [Ish92]. It relies on the minimization of the free energy which is modeled by a fourth order approach for the energy of the center ion stemming from the lattice cell and a coupling term describing the interaction between the ions of neighboring cells:
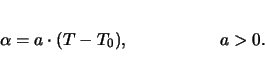 |
(3.6) |
| (3.7) |
| (3.8) |
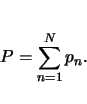 |
(3.9) |
The two allowed dipole moments are restricted by the
model to ![]() for the positive nuclei and
for the positive nuclei and ![]() for
the negative ones.
for
the negative ones.
![\resizebox{\fulllength}{!}{
\psfrag{P1}{$P_1$}
\psfrag{P2}{$P_2$}
\psfrag{P3}{$P...
...us}{negative nucleus}
\includegraphics[width=\fulllength]{figs/lattice_1d.eps}
}](img192.gif) |
The simulation starts at an equilibrium state where all the 'free'
dipoles are negatively polarized and the time-dependent expansion of
the domains that occurs around the nucleation centers is
examined. Therefore a viscosity coefficient ![]() is introduced
which takes into account the switching delay of the individual dipoles. The
resulting evolution of polarization is given by the Landau
Khalatnikov kinetic equation [Bau99]
is introduced
which takes into account the switching delay of the individual dipoles. The
resulting evolution of polarization is given by the Landau
Khalatnikov kinetic equation [Bau99]
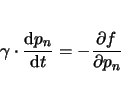 |
(3.10) |
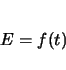 |
(3.12) |
This approach was extended to two-dimensional lattice structures by Omura et al. [OAI92] in 1992. The functional for the free energy had to be modified in order to include the increased number of possible coupling partners as follows
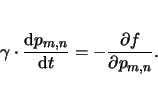 |
(3.15) |
This first approach did not consider the influence of the depolarization field. Instead the electric field was assumed to be constant in the entire simulation area. The influence of depolarization was finally added by Baudry in 1999 [Bau99], who implemented Poisson's equation into the system.
The basic intent of the free energy method is to gain insight into
the material properties and the main focus is the correct
qualitative reproduction of physical effects. Typical simulation
setups analyze areas of a size of about ![]() dipoles.
dipoles.