



Next: 3.2 Finite Volumes and
Up: 3. Mesh Generation
Previous: 3. Mesh Generation
3.1 Geometrical Mesh Quality
Well shaped elements are especially important for finite element methods.
Certain geometrical quality measures and ratios can be defined to
evaluate the shape of an element. Such purely geometrical criteria lead
by nature to an isotropic mesh density distribution. They are
implemented without the knowledge of the physical problem at hand.
Various types of not so well shaped elements are depicted in
Fig. 3.1.
Figure 3.1:
Various types of not so well shaped elements and some
parameters.
|
|
Some simple parameters of triangles in two dimensions and tetrahedra
in three dimensions are the edge lengths  , (dihedral) angles
, (dihedral) angles
 , volume
, volume  , circumsphere radius
, circumsphere radius  , insphere radius
, insphere radius
 , and normal distance
, and normal distance  of a vertex from its opposite
edge or triangle.
The height of an element is defined as
of a vertex from its opposite
edge or triangle.
The height of an element is defined as  .
It can be desirable to avoid elements with a too small height or
too obtuse (dihedral) angles. While such large angles are related to the
error of a finite element approximation, small angles can have a negative
effect on the condition number of the stiffness matrix
[5,80].
The following are some examples for the definition of an element measure
where greater values of
.
It can be desirable to avoid elements with a too small height or
too obtuse (dihedral) angles. While such large angles are related to the
error of a finite element approximation, small angles can have a negative
effect on the condition number of the stiffness matrix
[5,80].
The following are some examples for the definition of an element measure
where greater values of  denote a higher quality shape.
denote a higher quality shape.
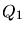 |
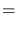 |
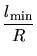 |
(3.1) |
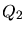 |
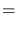 |
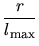 |
(3.2) |
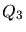 |
 |
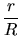 |
(3.3) |
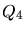 |
 |
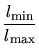 |
(3.4) |
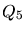 |
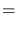 |
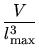 |
(3.5) |
To be more precise one has to note that not all of these definitions
provide a well behaved quality measure in all dimensions.
For example only  satisfy
satisfy
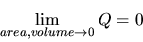 |
(3.6) |
 is actually the inverted aspect ratio as it is commonly
defined for three-dimensional elements.
is actually the inverted aspect ratio as it is commonly
defined for three-dimensional elements.
 has been used by [8,87].
has been used by [8,87].  behaves well in two dimensions, but it is inapt
to capture the shape of three-dimensional sliver elements as depicted in
Fig. 3.1. The volume of such a sliver element can be made
arbitrarily small while at the same time
behaves well in two dimensions, but it is inapt
to capture the shape of three-dimensional sliver elements as depicted in
Fig. 3.1. The volume of such a sliver element can be made
arbitrarily small while at the same time  remains a positive
constant. The dihedral angles of the sliver element can be changed to the
better or to the worse while the measure
remains a positive
constant. The dihedral angles of the sliver element can be changed to the
better or to the worse while the measure  can be kept constant.
One can gradually transform a well shaped element into a sliver
element by moving one vertex without changing
can be kept constant.
One can gradually transform a well shaped element into a sliver
element by moving one vertex without changing  and hence
without changing
and hence
without changing  .
This interesting fact follows from the important relation between
the angles of an element and its
.
This interesting fact follows from the important relation between
the angles of an element and its  parameters.
Only in two dimensions it is possible to derive a formula for triangles
which describes the relation between the edge length and its opposite angle
(Fig. 3.2 and Fig. 3.3).
parameters.
Only in two dimensions it is possible to derive a formula for triangles
which describes the relation between the edge length and its opposite angle
(Fig. 3.2 and Fig. 3.3).
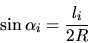 |
(3.7) |
Figure 3.2:
The relation between the edge length and its opposite angle in a
triangle follows from
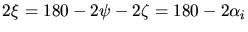 and therefore
and therefore
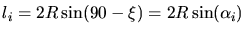 .
.
|
|
Figure 3.3:
With constant edge length and circumsphere radius the opposite
dihedral angle in a tetrahedron can have arbitrary values.
|
|
Assuming that  is constant, the smallest angle will correspond to
the shortest edge. Hence, a minimum bound for
is constant, the smallest angle will correspond to
the shortest edge. Hence, a minimum bound for  also is a bound to
the smallest angle in the triangle.
Lacking this relationship in three dimensions many quality criteria fail to
guarantee bounded dihedral angles.
also is a bound to
the smallest angle in the triangle.
Lacking this relationship in three dimensions many quality criteria fail to
guarantee bounded dihedral angles.
 has more the nature of a one-dimensional measure. It fails even in
two dimensions to avoid badly shaped triangles. With a fixed
has more the nature of a one-dimensional measure. It fails even in
two dimensions to avoid badly shaped triangles. With a fixed  a
triangle may have any obtuse angle.
It will depend on the application whether or not angles are important and
which criteria prove to be useful.
a
triangle may have any obtuse angle.
It will depend on the application whether or not angles are important and
which criteria prove to be useful.
An important conclusion can be drawn. Whatever means are pursued to
improve the element quality, the employed technique must fit to the applied
measure. Otherwise termination is not ensured. If the number of
needles and caps should be reduced by means of refinement but
the number of slivers by local transformations, the former must be
distinguished from the latter.
The refinement should then be controlled by e.g.  which will not
detect the slivers. And the local transformations could be applied in a
following step for elements which do not comply with e.g.
which will not
detect the slivers. And the local transformations could be applied in a
following step for elements which do not comply with e.g.  .
.




Next: 3.2 Finite Volumes and
Up: 3. Mesh Generation
Previous: 3. Mesh Generation
Peter Fleischmann
2000-01-20
![\includegraphics [width=0.8\textwidth]{ppl/slivergen.ps}](img33.gif)
![]() , (dihedral) angles
, (dihedral) angles
![]() , volume
, volume ![]() , circumsphere radius
, circumsphere radius ![]() , insphere radius
, insphere radius
![]() , and normal distance
, and normal distance ![]() of a vertex from its opposite
edge or triangle.
The height of an element is defined as
of a vertex from its opposite
edge or triangle.
The height of an element is defined as ![]() .
It can be desirable to avoid elements with a too small height or
too obtuse (dihedral) angles. While such large angles are related to the
error of a finite element approximation, small angles can have a negative
effect on the condition number of the stiffness matrix
[5,80].
The following are some examples for the definition of an element measure
where greater values of
.
It can be desirable to avoid elements with a too small height or
too obtuse (dihedral) angles. While such large angles are related to the
error of a finite element approximation, small angles can have a negative
effect on the condition number of the stiffness matrix
[5,80].
The following are some examples for the definition of an element measure
where greater values of ![]() denote a higher quality shape.
denote a higher quality shape.
![\includegraphics [width=0.45\textwidth]{ppl/edgeanglerel.ps}](img61.gif)
![\includegraphics [width=0.45\textwidth]{ppl/edgeangle3d.eps}](img63.gif)
![]() which will not
detect the slivers. And the local transformations could be applied in a
following step for elements which do not comply with e.g.
which will not
detect the slivers. And the local transformations could be applied in a
following step for elements which do not comply with e.g. ![]() .
.