A quasi-bound state forms if one of the system boundary conditions is open
(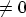 ) and the other one is closed (
) and the other one is closed (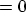 ). The carrier wave function is
reflected at the interface, there is no transmitted wave. Using the
transfer-matrix method described in Section 3.5.3, the system can be described
by
). The carrier wave function is
reflected at the interface, there is no transmitted wave. Using the
transfer-matrix method described in Section 3.5.3, the system can be described
by
where the wave functions are plane waves
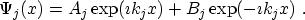 |
(3.109) |
However, no transmission coefficient can be defined for a quasi-bound state:
The transmitted wave amplitude
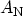 must vanish to fulfill the assumption of
closed boundary conditions. Instead, a reflection coefficient can be defined
which is
must vanish to fulfill the assumption of
closed boundary conditions. Instead, a reflection coefficient can be defined
which is
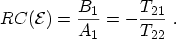 |
(3.110) |
It is shown in [165] that for a quasi-bound state, the transfer
matrix is not HERMITian3.9 and its elements obey
Therefore, the reflection coefficient
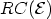 can be written as
can be written as
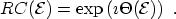 |
(3.111) |
The phase
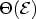 varies only weakly at energies away from the
resonance energy of the QBS, while near the QBS the phase changes
strongly. Near the complex energy levels
varies only weakly at energies away from the
resonance energy of the QBS, while near the QBS the phase changes
strongly. Near the complex energy levels
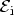 the derivative of the phase
factor
the derivative of the phase
factor
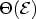 follows a LORENTZian3.10 distribution
follows a LORENTZian3.10 distribution
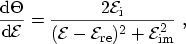 |
(3.112) |
where
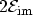 is the full-width half-maximum (FWHM) value of
is the full-width half-maximum (FWHM) value of
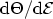 . Thus, by calculating the phase of the reflection
coefficient as a function of energy, the life times can be determined. This
method has been studied intensely by CASSAN et al. [160,175]. They
reported numerical difficulties in the calculation of the value of
. Thus, by calculating the phase of the reflection
coefficient as a function of energy, the life times can be determined. This
method has been studied intensely by CASSAN et al. [160,175]. They
reported numerical difficulties in the calculation of the value of
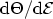 which is prone to numerical noise. Similar problems
have been reported by other groups [176].
which is prone to numerical noise. Similar problems
have been reported by other groups [176].
An alternative approach has been presented by CLERC et al. who noted
that the life times can also be extracted directly from the transfer
matrix [144]. For a free state,
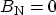 in (3.108) and the
transmission coefficient becomes
in (3.108) and the
transmission coefficient becomes
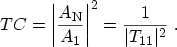 |
(3.113) |
For a quasi-bound state,
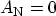 . Therefore,
. Therefore,
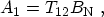 |
(3.114) |
but, since
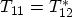 , the value of
, the value of
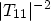 may be evaluated
as well -- even if it cannot be interpreted as a transmission
coefficient. The life time of the QBS is again found from the resonance peak
of the LORENTZian around the real component of the eigenenergy
may be evaluated
as well -- even if it cannot be interpreted as a transmission
coefficient. The life time of the QBS is again found from the resonance peak
of the LORENTZian around the real component of the eigenenergy
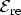
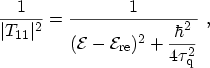 |
(3.115) |
but no derivative must be calculated this time. As an example of this method
the left part of Fig. 3.14 shows the shape of the conduction band edge of a
MOS structure in the substrate, dielectric, and polysilicon gate. In the
substrate a triangular quantum well forms. Considering closed boundaries,
eigenvalues and wave functions can be calculated. The corresponding wave
functions are shown in the figure, where closed boundary conditions have been
used at the boundaries of the simulation domain. Note the wave function
penetration into the classically forbidden region of the dielectric layer. The
eigenvalues of the quasi-bound states are located at 0.27, 0.47, 0.63, 0.76,
0.86, and 0.95eV. The same information can be found when the value of
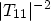 is investigated, as shown in right part of Fig. 3.14: Every
quasi-bound state in the inversion layer manifests as a peak in the value of
is investigated, as shown in right part of Fig. 3.14: Every
quasi-bound state in the inversion layer manifests as a peak in the value of
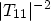 . The width of each peak is directly related to its life time.
. The width of each peak is directly related to its life time.
Figure 3.14:
Wave function of quasi-bound states. Note the wave
function penetration into classically forbidden regions (left). The respective
value of
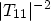 as a function of energy is shown in the right
plot. The energy broadening around the poles is clearly visible.
as a function of energy is shown in the right
plot. The energy broadening around the poles is clearly visible.
|
|
A. Gehring: Simulation of Tunneling in Semiconductor Devices
![]() ) and the other one is closed (
) and the other one is closed (![]() ). The carrier wave function is
reflected at the interface, there is no transmitted wave. Using the
transfer-matrix method described in Section 3.5.3, the system can be described
by
). The carrier wave function is
reflected at the interface, there is no transmitted wave. Using the
transfer-matrix method described in Section 3.5.3, the system can be described
by
![]() in (3.108) and the
transmission coefficient becomes
in (3.108) and the
transmission coefficient becomes
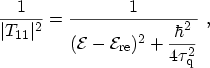
![\includegraphics[width=.48\linewidth]{figures/barrierClosedWave}](img566.png)
![\includegraphics[width=.48\linewidth]{figures/lifetimes}](img567.png)