|
|
|
|
Previous: 2.3 Systematic Approach Up: 2.3 Systematic Approach Next: 2.3.2 Moments Method |
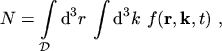 |
(2.43) |
In the semiclassical picture it is assumed that the state of a carrier at
![]() in phase space is well defined at each time
in phase space is well defined at each time ![]() . This statement violates the
uncertainty principle formulated by HEISENBERG according to which both the position
and the momentum of the carrier cannot be specified at the same time. However, in most
transport problems of interest, the location of the carriers need only be fixed on a
macroscopic scale [14, p.131]. To account for quantum effects, equations
based on the WIGNER-BOLTZMANN equation have been considered [15].
. This statement violates the
uncertainty principle formulated by HEISENBERG according to which both the position
and the momentum of the carrier cannot be specified at the same time. However, in most
transport problems of interest, the location of the carriers need only be fixed on a
macroscopic scale [14, p.131]. To account for quantum effects, equations
based on the WIGNER-BOLTZMANN equation have been considered [15].
From a practical point of view, the direct solution of BTE by a deterministic method is an extremely demanding and often un-practical task. The Monte Carlo method provides an accurate solution of this equation. However, the computational demand of this method is often too high to be used for TCAD purposes. Also, if the distribution of high-energetic carriers is relevant, or if the carrier concentration is very low in specific regions of the device, Monte Carlo simulations tend to produce high variance in the results. Therefore, further approximations can be introduced in order to derive simpler equations from BTE and to obtain a reasonable trade-off between physical accuracy and computational demand.
M. Gritsch: Numerical Modeling of Silicon-on-Insulator MOSFETs PDF