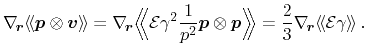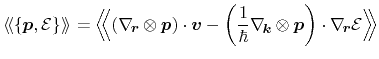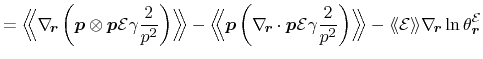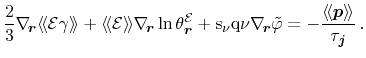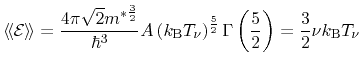In the following, the derivation of the particle flux equation is performed
analogously to Stratton's approach. The starting point is again the Boltzmann transport equation
with a general weight
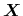 in the form of equation (3.30). Inserting
in the form of equation (3.30). Inserting
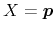 as
as
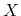 yields
yields
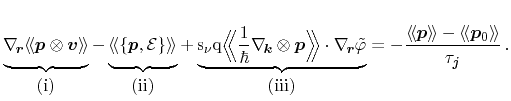 |
(3.80) |
Application of the trace approximation of tensor valued expressions
(3.39) as well as a product ansatz for the energy as presented in
equation (3.40) on term (i) results in
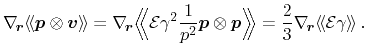 |
(3.81) |
The Poisson bracket within the average in (ii) has to be expanded using
(A.6). Furthermore, the inverse product rule (B.3) is used
to transform the
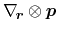 - term in the first term. The product ansatz
for the energy as well as the trace approximation result in
- term in the first term. The product ansatz
for the energy as well as the trace approximation result in
The third term (iii) can be handled in a straight-forward manner. Assembly
of all three terms leads to
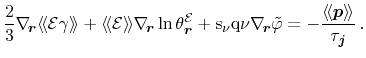 |
(3.83) |
Assuming parabolic bands and a heated, displaced Maxwellian,
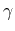 becomes
unity and the average reads
becomes
unity and the average reads
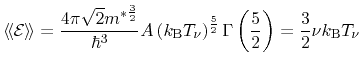 |
(3.84) |
normalized with the carrier concentration (3.54). Summation over all
parts as well as the mobility definition consistent with the homogeneous case
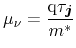 |
(3.85) |
yields the final form of the particle current equation
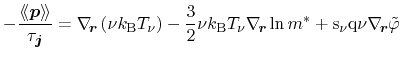 |
|
|
(3.86) |
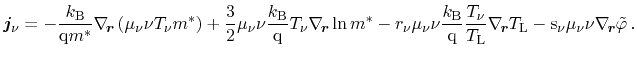 |
|
|
(3.87) |
Rewriting the particle current equation with the electrochemical potential
defined in Eqs. (3.60) and (3.62) results in
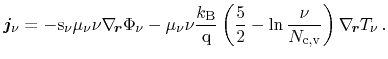 |
(3.88) |
M. Wagner: Simulation of Thermoelectric Devices
![]() in the form of equation (3.30). Inserting
in the form of equation (3.30). Inserting
![]() as
as
![]() yields
yields