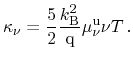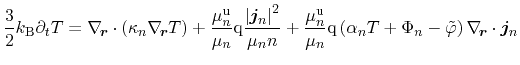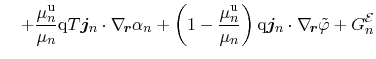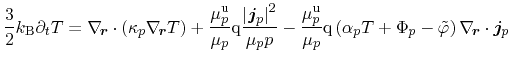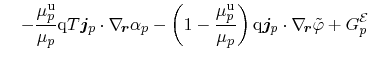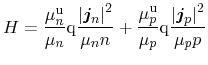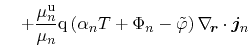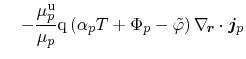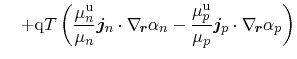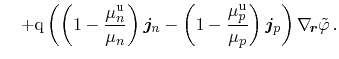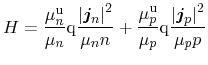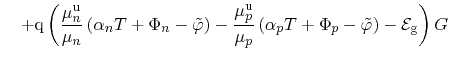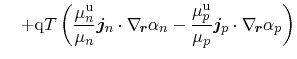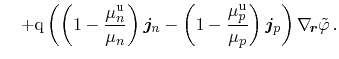3.5.10 Electrothermal Transport Model
For the simulation of thermoelectric devices, it is important to accurately
describe the energy relations within the device. In the electrothermal
transport model, the contributions of the carrier subsystems and the lattice
are combined to one heat-flux equation, whereby a rigorous treatment of the
coupling mechanisms between the thermal and the electrical description is
achieved.
Since the driving forces within thermoelectric devices are very low compared to
modern CMOS devices, the carrier gas can be safely assumed to be in local
thermodynamic equilibrium with the lattice. Thus, the inclusion of additional
equations accounting for carriers driven far from equilibrium to the
constituent equation system are an unnecessary computational overhead.
Assuming local thermodynamic equilibrium, the electrothermal transport model
can be obtained from the energy transport model as a starting point.
Besides Poisson's equation, the electrothermal transport model incorporates
carrier balance equations as well as current equations for both electrons and
holes. The energy relations are described by an additional heat-flow
equation, which is accessible from both a systematic and a phenomenological
point of view.
In the sequel, the electrothermal transport model is governed based on the
moment equations derived by Bløtekjær's approach. The calculation with
Stratton's equations is similar, and includes additional terms accounting
for the scattering parameters
 . The energy flux equation derived after
Bløtekjær (3.122) assuming local thermal equilibrium expressed in
terms of the particle flux reads
. The energy flux equation derived after
Bløtekjær (3.122) assuming local thermal equilibrium expressed in
terms of the particle flux reads
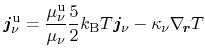 |
(3.149) |
with the thermal conductivity
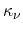 of the carrier subsystem obeying a
Wiedemann-Franz law
of the carrier subsystem obeying a
Wiedemann-Franz law
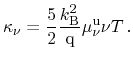 |
(3.150) |
In (3.149), the two contributions to the energy flux by a
moving carrier gas as well as heat conduction by the carrier gas can be
identified. However, in non-degenerate semiconductors, the thermal
conductivities of the carrier subsystems can be neglected against the lattice
contribution [95]. Insertion of (3.149) into the
energy balance equation (3.65) yields
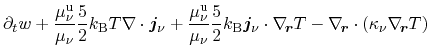 |
|
|
(3.151) |
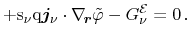 |
|
|
|
In order to obtain expressions accessible by physical interpretation, a few
rearrangements have to be performed on (3.151). First, the
gradient of the electrochemical potential has to be substituted by the current
relation (3.88)
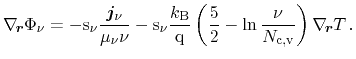 |
(3.152) |
Furthermore, the Seebeck coefficient
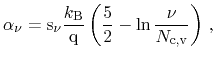 |
(3.153) |
is introduced which is described closer in Section 3.5.12. Inserting
(3.152) and (3.153) to (3.151) yields
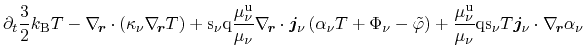 |
|
|
(3.154) |
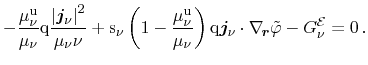 |
|
|
|
Equation (3.154) denotes the energy balance equation for the
electron and hole subsystem, respectively. The lattice contribution
incorporates an additional heat flux term, which is the dominant contribution
to heat conduction within most moderately doped semiconductors. This heat flux
is expressed by a Fourier law with the according lattice heat conductivity
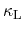 . The energy balance equations for the three subsystems read
. The energy balance equations for the three subsystems read
The final heat-flow equation is governed as the sum of the contributions of
all three subsystems. Both specific heat and thermal conductivity are
expressed as parameters for the entire semiconductor. Thus, the heat-flow
equation reads
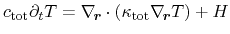 |
(3.158) |
with the heat source term
For the stationary case, the divergence terms of the electron and hole currents
can be expressed by the net recombination rate due to the vanishing
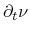 -term in the carrier balance equation (3.37). For this special case,
the heat source term becomes
-term in the carrier balance equation (3.37). For this special case,
the heat source term becomes
An often used, but not fully justifiable assumption is that the mobility ratios
equal unity for each electrons and holes [86]. Therefore, the heat
source term reduces to
The contributions to equation (3.161) are the Joule
heat losses due to current flow throughout the structure, the recombination
heat, which is transferred to the lattice due to carrier recombination, and the
Thomson heat. This expression is compatible to an approach based on
considerations of phenomenological irreversible thermodynamics, which is
summarized in the following section.
M. Wagner: Simulation of Thermoelectric Devices
![]() . The energy flux equation derived after
Bløtekjær (3.122) assuming local thermal equilibrium expressed in
terms of the particle flux reads
. The energy flux equation derived after
Bløtekjær (3.122) assuming local thermal equilibrium expressed in
terms of the particle flux reads